【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,メカトロニクスのデジタル制御に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。
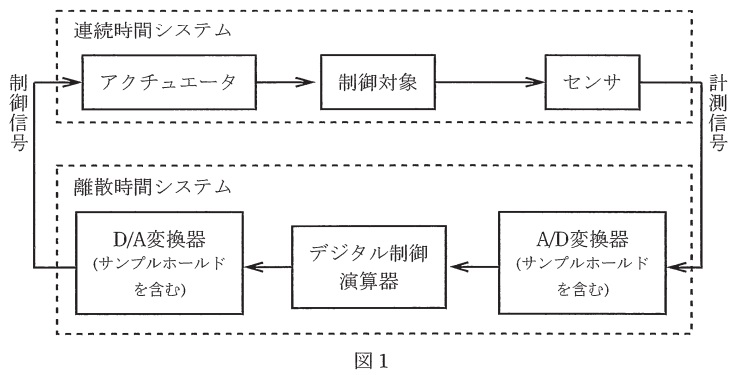
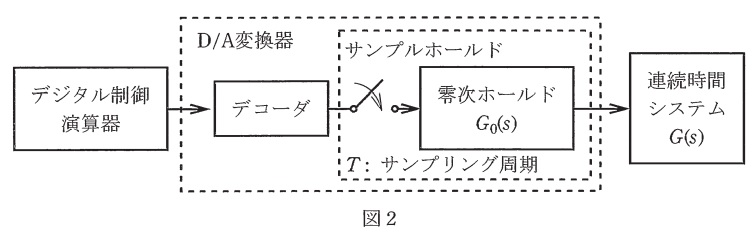
メカトロニクス装置は,コンピュータやエレクトロニクスを駆使した高度化された機械である。メカトロニクスシステムの基本構成は,制御対象である連続時間システムとデジタル制御である離散時間システムとが含まれる図1に示すような構成が一般的である。このようなシステムは,デジタル制御演算器からみたモデルとして,\( \ \fbox { (1) } \ \)を用いてパルス伝達関数で表現することによって,制御対象とデジタル制御演算器とが統一的に解析できる。すなわち,図2のサンプリング周期\( \ T \ \)をもつ\( \ \mathrm {D / A} \ \)変換器で,零次ホールド要素\( \ G_{0} ( s ) \ \)と伝達関数\( \ G ( s ) \ \)とをカスケード結合している連続時間システムに対するパルス伝達関数\( \ G^{*}( z ) \ \)は,
\[
\begin{eqnarray}
G_{0} ( s )&=&\fbox { (2) } \\[ 5pt ]
\end{eqnarray}
\]
であるので,
\[
\begin{eqnarray}
G^{*}( z )&=&Z\left[ G_{0} ( s )G ( s ) \right] &=&\left( 1-z^{-1}\right) Z\left[ \frac {G ( s ) }{s}\right] \\[ 5pt ]
\end{eqnarray}
\]
と表現できる。同様に,デジタル制御演算器に合わせて図1の\( \ \mathrm {A / D} \ \)変換器もパルス伝達関数で表現することによって統一的な解析が可能である。
このような解析において,\( \ \mathrm {A / D} \ \)変換器の前段では,サンプリング周波数の\( \ \displaystyle \frac {1}{2} \ \)の周波数である\( \ \fbox { (3) } \ \)周波数と呼ばれる周波数以上の成分を,急峻(きゅうしゅん)に減衰させるフィルタを設けることで\( \ \fbox { (4) } \ \)現象を防止することを前提としている。さらに,対象となる\( \ \mathrm {A / D} \ \)変換器では,アナログ量をサンプリングして有限のビット数からなるデジタル値に変換することによる\( \ \fbox { (5) } \ \)誤差が無視できることを前提に扱われている。
〔問7の解答群〕
\[
\begin{eqnarray}
&(イ)& フェランチ &(ロ)& 拡 大 &(ハ)& \mathrm {z}変換 \\[ 5pt ]
&(ニ)& \frac {1+\mathrm {e}^{-sT}}{s} &(ホ)& \frac {1-\mathrm {e}^{-sT}}{s} &(ヘ)& ステップ \\[ 5pt ]
&(ト)& サンプリング &(チ)& ナイキスト &(リ)& カットオフ \\[ 5pt ]
&(ヌ)& 等価変換 &(ル)& エイリアシング &(ヲ)& \frac {1-\mathrm {e}^{sT}}{s} \\[ 5pt ]
&(ワ)& 時間変換 &(カ)& ビット化 &(ヨ)& 量子化
\end{eqnarray}
\]
【ワンポイント解説】
情報処理に関するかなり専門性の高い分野からの出題です。知っていればそれほど難しい問題ではありません。情報処理の概念を理解する上では良い問題であると思いますが,電験の問題としては再出題の可能性は低いと思います。
1.ディジタル伝送方式
ディジタル伝送方式は,アナログ量である情報をデジタル量に変換(\( \ \mathrm {A / D} \ \)変換)してから情報を伝送する仕組みで,下記のような過程を経て情報を伝送します。
①標本化(サンプリング)
アナログ量の大きさを一定周期\( \ T \ \)ごとに読み取り,期間\(T\)の間はその値が一定であるようにすることです。\( \ \displaystyle \frac {1}{T} \ \)をサンプリング周波数と言います。サンプリング周波数の\( \ \displaystyle \frac {1}{2} \ \)以上の周波数(ナイキスト周波数)を持つと,折り返し誤差が発生する(エイリアシング現象)ので,フィルタで除去する必要があります。
②量子化
標本化した情報を\( \ \mathrm {A / D} \ \)変換器でデジタル値に変換することを言います。
③符号化
量子化した情報をサンプリング周波数毎のパルス化することを言います。
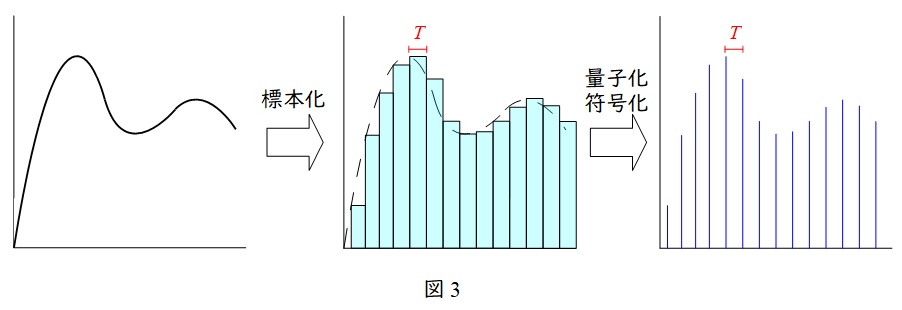
2.\( \ \mathrm {z} \ \)変換
下式で定義される,連続量を離散化(上記図3の右側の図)させるような変換で,イメージとしてはラプラス変換に似ています。しっかりと理解するためにはフーリエ変換の教科書から理解する必要があります。電験では計算は出題されないので,名称とイメージだけ覚えておけば良いと思います。
\[
\begin{eqnarray}
F \left( z\right) &=&\sum _{n=0}^{\infty } f \left( n\right) z^{-n} \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(1)解答:ハ
題意より,解答候補は(ハ)\( \ \mathrm {z} \ \)変換,(ヌ)等価変換,(ワ)時間変換,になると思います。ワンポイント解説「2.\( \ \mathrm {z} \ \)変換」の通り,連続量を離散化させるため\( \ \mathrm {z} \ \)変換を用います。
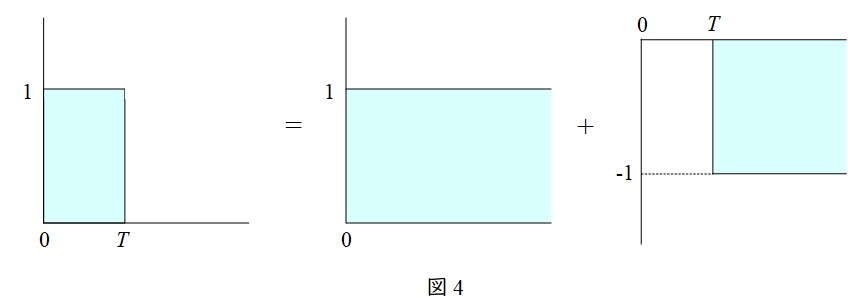
(2)解答:ホ
零次ホールド要素は図4左に示すように周期\( \ T \ \)の単位パルスとなります。単位パルス\( \ g _{0} (t ) \ \)は,
\[
\begin{eqnarray}
g _{0} (t ) &=&u ( t ) – u (t – T ) \\[ 5pt ]
\end{eqnarray}
\]
となり,ラプラス変換すると,
\[
\begin{eqnarray}
G _{0} (s ) &=&\frac {1}{s} – \frac {1}{s} \mathrm {e}^{-sT} \\[ 5pt ]
&=&\frac {1-\mathrm {e}^{-sT}}{s} \\[ 5pt ]
\end{eqnarray}
\]
となります。
(3)解答:チ
ワンポイント解説「1.ディジタル伝送方式」の通り,ナイキスト周波数となります。
(4)解答:ル
ワンポイント解説「1.ディジタル伝送方式」の通り,エイリアシング現象となります。
(5)解答:ヨ
ワンポイント解説「1.ディジタル伝送方式」の通り,アナログ量をサンプリングして有限のビット数からなるデジタル値に変換することを量子化と言い,量子化誤差はサンプリング周期が大きい場合に発生しやすくなります。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん