《機械》〈回転機〉[H27:問2] 同期機の時定数に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★★（難しい）

次の文章は，同期機の時定数に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。

同期機の過渡現象計算に用いられる時定数は，以下で扱う電流の初期過渡，過渡及び直流の変化成分の初期値からの変化量が初期値から最終値までの変化量の$ \ \fbox {　（１）　} \ ％ \ $となるのに要する時間である。

直軸開路初期過渡時定数$ \ T_{\mathrm {d0}}^{\prime \prime} \ $は電機子巻線開路時の直軸$ \ \fbox {　（２）　} \ $開路時定数であり，直軸短絡初期過渡時定数$ \ T_{\mathrm {d}}^{\prime \prime} \ $は電機子巻線閉路時の直軸$ \ \fbox {　（２）　} \ $開路時定数である。$ \ T_{\mathrm {d}}^{\prime \prime} \ $は三相突発短絡電流の交流分の最初の数サイクル(初期過渡)の急激な減衰を定める時定数であり，$ \ T_{\mathrm {d}}^{\prime \prime}= \ \fbox {　（３）　} \ \times T_{\mathrm {d0}}^{\prime \prime} \ $となる。

直軸開路時定数$ \ T_{\mathrm {d0}}^{\prime} \ $は電機子巻線開路時の界磁回路時定数であり，直軸短絡過渡時定数$ \ T_{\mathrm {d}}^{\prime} \ $は電機子巻線閉路時の界磁回路時定数である。$ \ T_{\mathrm {d}}^{\prime} \ $は三相突発短絡電流の交流分から前述の初期過渡の急激な減衰電流を除外した電流の減衰を定める時定数であり，$ \ T_{\mathrm {d}}^{\prime}= \ \fbox {　（４）　} \ \times T_{\mathrm {d0}}^{\prime} \ $となる。

電機子時定数$ \ T_{\mathrm {a}} \ $は，電機子回路の直流分電流に対する時定数で，突発短絡電流の直流分の減衰を定める時定数であり，
\[
T_{\mathrm {a}}=\frac {\fbox {　（５）　}}{2\pi fR_{\mathrm {a}}}
\] となる。ただし，$ \ f \ $は周波数，$ \ R_{\mathrm {a}} \ $は電機子巻線抵抗である。

なお，解答群において，$ \ X_{\mathrm {d}}^{\prime \prime} \ $は直軸初期過渡リアクタンス，$ \ X_{\mathrm {d}}^{\prime } \ $は直軸過渡リアクタンス，$ \ X_{\mathrm {d}} \ $は直軸同期リアクタンス，$ \ X_{1} \ $は正相リアクタンス，$ \ X_{2} \ $は逆相リアクタンス，$ \ X_{0} \ $は零相リアクタンスである。

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　制動巻線　　　　　&（ロ）&　一次巻線　　　　　&（ハ）&　X_{0} \\[ 5pt ] &（ニ）&　50　　　　　&（ホ）&　\frac {X_{\mathrm {d}}^{\prime }}{X_{\mathrm {d}}^{\prime }+X_{\mathrm {d}}^{\prime \prime }}　　　　　&（ヘ）&　\frac {X_{\mathrm {d}}^{\prime }}{X_{\mathrm {d}}} \\[ 5pt ] &（ト）&　\frac {X_{\mathrm {d}}^{\prime }}{X_{\mathrm {d}}+X_{\mathrm {d}}^{\prime }}　　　　　&（チ）&　63.2　　　　　&（リ）&　\frac {X_{\mathrm {d}}^{\prime \prime}}{X_{\mathrm {d}}^{\prime }+X_{\mathrm {d}}^{\prime \prime }} \\[ 5pt ] &（ヌ）&　\frac {X_{\mathrm {d}}^{\prime \prime}}{X_{\mathrm {d}}^{\prime }}　　　　　&（ル）&　\frac {X_{\mathrm {d}}}{X_{\mathrm {d}}+X_{\mathrm {d}}^{\prime }}　　　　　&（ヲ）&　二次巻線 \\[ 5pt ] &（ワ）&　X_{1}　　　　　&（カ）&　36.8　　　　　&（ヨ）&　X_{2} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

同期機の過渡現象を理解する上で，直軸(d軸)成分の等価回路と横軸(q軸)成分の等価回路は必須となります。電験二種ではまず出てこない新しい内容となります。このホームページではその概要について触れますが，詳細に説明すると何十ページにもなってしまうので，もう少し理解が必要ならば，専門書を一読することをオススメします。(3)，(4)は模範解答として計算を載せていますが，実質的には暗記していなければ解けないと思います。

1.同期機の$ \ \mathrm {d} \ $軸成分等価回路と$ \ \mathrm {q} \ $軸成分等価回路
同期機の回転子の磁極と同じ向きの軸を直軸($ \ \mathrm {d} \ $軸)，磁極と直角の向きの軸を横軸($ \ \mathrm {q} \ $軸)としたときの等価回路は図2，図3となります。

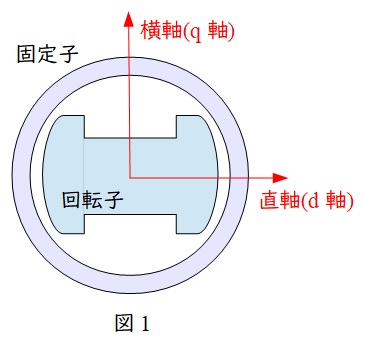
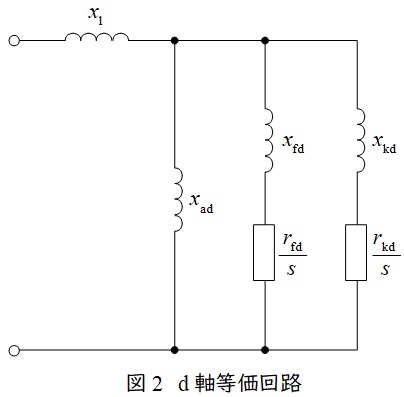
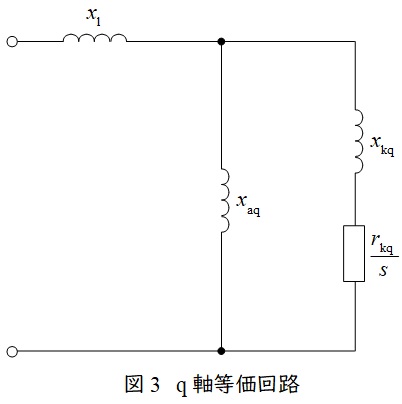
$ \ x_{\mathrm {l}} \ $：電機子巻線漏れリアクタンス，　$ \ x_{\mathrm {ad}}，x_{\mathrm {aq}} \ $：電機子反作用リアクタンス
$ \ r_{\mathrm {fd}} \ $：界磁巻線抵抗，　$ \ x_{\mathrm {fd}} \ $：界磁巻線リアクタンス
$ \ r_{\mathrm {kd}}，r_{\mathrm {kq}} \ $：制動巻線抵抗，　$ \ x_{\mathrm {kd}}，x_{\mathrm {kq}} \ $：制動巻線リアクタンス
$ \ s \ $：ラプラス演算子

2.初期過渡リアクタンス$ \ X_{\mathrm {d}}^{\prime \prime} \ $と過渡リアクタンス$ \ X_{\mathrm {d}}^{\prime} \ $，同期リアクタンス$ \ X_{\mathrm {d}} \ $
図2において，過渡現象が始まって数サイクルの間は$ \ s \ $が非常に大きく，界磁巻線抵抗及び制動巻線抵抗とも無視できるほど小さくなるので，界磁巻線リアクタンスと制動巻線リアクタンスを考慮します。これを初期過渡リアクタンスと呼びます。

次に数サイクル～$ \ 1.0 \ $秒程度の間は$ \ s \ $は少し小さくなり，$ \ r_{\mathrm {fd}} \ ＜ \ r_{\mathrm {kd}} \ $ため，界磁巻線抵抗は無視できますが制動巻線抵抗は無視できなくなるので，界磁巻線リアクタンスと電機子のリアクタンスを考慮すれば良くなります。これを過渡リアクタンスと呼びます。

1.0秒以降は$ \ s \ $の値が小さくなるので，界磁巻線抵抗及び制動巻線抵抗が無視できなくなるので，電機子のリアクタンスのみ考慮すればよくなります。これを同期リアクタンスと呼びます。

【解答】

(1)解答：チ
時定数は初期値の$ \ \displaystyle \frac {1}{\mathrm {e}} \ $になったときの変化量の値である。$ \ \mathrm {e}≒2.718 \ $を考慮すると変化量は，
\[
\begin{eqnarray}
1-\frac {1}{\mathrm {e}}&=&1-\frac {1}{2.718} \\[ 5pt ] &≒&0.632 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：イ
d軸等価回路は図2の通り表されるが，一般に$ \ x_{\mathrm {kd}} \ ＜ \ x_{\mathrm {fd}} \ $であるため，過渡現象の初期では制動巻線の影響が大きい。よって制動巻線が正しい解答となる。

(3)解答：ヌ
直軸開路初期過渡時定数$ \ T_{\mathrm {d0}}^{\prime \prime} \ $は図2の回路そのものの時定数であり，$ \ r_{\mathrm {kd}} \ ＞ \ r_{\mathrm {fd}} \ $となるため，$ \ r_{\mathrm {fd}} \ $を無視できる。よって，$ \ r_{\mathrm {kd}} \ $において減衰される時定数$ \ T_{\mathrm {d0}}^{\prime \prime} \ $は，
\[
T_{\mathrm {d0}}^{\prime \prime}=\frac {\displaystyle x_{\mathrm {kd}}+\frac {1}{\displaystyle \frac {1}{x_{\mathrm {fd}}}+\frac {1}{x_{\mathrm {ad}}}}}{2\pi f r_{\mathrm {kd}}}
\] となる。直軸短絡初期過渡時定数$ \ T_{\mathrm {d}}^{\prime \prime} \ $は図2の左端を短絡した時の$ \ r_{\mathrm {kd}} \ $において減衰される時定数であるので，
\[
T_{\mathrm {d}}^{\prime \prime}=\frac {\displaystyle x_{\mathrm {kd}}+\frac {1}{\displaystyle \frac {1}{x_{\mathrm {fd}}}+\frac {1}{x_{\mathrm {ad}}}+\frac {1}{x_{\mathrm {l}}}}}{2\pi f r_{\mathrm {kd}}}
\] となる。よってその比は，
\[
\begin{eqnarray}
\frac {T_{\mathrm {d}}^{\prime \prime}}{T_{\mathrm {d0}}^{\prime \prime}}&=&\frac {\frac {\displaystyle x_{\mathrm {kd}}+\frac {1}{\displaystyle \frac {1}{x_{\mathrm {fd}}}+\frac {1}{x_{\mathrm {ad}}}+\frac {1}{x_{\mathrm {l}}}}}{\displaystyle 2\pi f r_{\mathrm {kd}}}}{\frac {\displaystyle x_{\mathrm {kd}}+\frac {1}{\displaystyle \frac {1}{x_{\mathrm {fd}}}+\frac {1}{x_{\mathrm {ad}}}}}{\displaystyle 2\pi f r_{\mathrm {kd}}}} \\[ 5pt ] &=&\frac {\displaystyle x_{\mathrm {kd}}+\frac {1}{\displaystyle \frac {1}{\displaystyle x_{\mathrm {fd}}}+\frac {1}{x_{\mathrm {ad}}}+\frac {1}{x_{\mathrm {l}}}}}{\displaystyle x_{\mathrm {kd}}+\frac {1}{\displaystyle \frac {1}{x_{\mathrm {fd}}}+\frac {1}{x_{\mathrm {ad}}}}} \\[ 5pt ] \end{eqnarray}
\] となり，$ \ \displaystyle X=\frac {1}{\displaystyle \frac {1}{x_{\mathrm {fd}}}+\frac {1}{x_{\mathrm {ad}}}} \ $とおくと，
\[
\begin{eqnarray}
\frac {T_{\mathrm {d}}^{\prime \prime}}{T_{\mathrm {d0}}^{\prime \prime}}&=&\frac {\displaystyle x_{\mathrm {kd}}+\frac {1}{\displaystyle \frac {1}{X}+\frac {1}{x_{\mathrm {l}}}}}{\displaystyle x_{\mathrm {kd}}+X} \\[ 5pt ] &=&\frac {\displaystyle x_{\mathrm {kd}}( x_{\mathrm {l}}+X)+Xx_{\mathrm {l}}}{\displaystyle (x_{\mathrm {kd}}+X ) ( x_{\mathrm {l}}+X)} \\[ 5pt ] &=&\frac {\displaystyle x_{\mathrm {kd}}x_{\mathrm {l}}+Xx_{\mathrm {kd}}+Xx_{\mathrm {l}}}{\displaystyle (x_{\mathrm {kd}}+X ) ( x_{\mathrm {l}}+X)} \\[ 5pt ] &=&\frac {\displaystyle x_{\mathrm {l}}(x_{\mathrm {kd}}+X)+Xx_{\mathrm {kd}}}{\displaystyle (x_{\mathrm {kd}}+X ) ( x_{\mathrm {l}}+X)} \\[ 5pt ] &=&\frac {\displaystyle x_{\mathrm {l}}+\frac {Xx_{\mathrm {kd}}}{x_{\mathrm {kd}}+X }}{\displaystyle x_{\mathrm {l}}+X} \\[ 5pt ] &=&\frac {\displaystyle x_{\mathrm {l}}+\frac {1}{\displaystyle \frac {1}{x_{\mathrm {kd}}}+\frac {1}{X}} }{\displaystyle x_{\mathrm {l}}+X} \\[ 5pt ] &=&\frac {\displaystyle x_{\mathrm {l}}+\frac {1}{\displaystyle \frac {1}{x_{\mathrm {kd}}}+\frac {1}{x_{\mathrm {fd}}}+\frac {1}{x_{\mathrm {ad}}}} }{\displaystyle x_{\mathrm {l}}+\frac {1}{\displaystyle \frac {1}{x_{\mathrm {fd}}}+\frac {1}{x_{\mathrm {ad}}}}} \\[ 5pt ] \end{eqnarray}
\] ここで，ワンポイント解説「2.初期過渡リアクタンス$ \ X_{\mathrm {d}}^{\prime \prime} \ $と過渡リアクタンス$ \ X_{\mathrm {d}}^{\prime} \ $，同期リアクタンス$ \ X_{\mathrm {d}} \ $」より，
\[
\begin{eqnarray}
X_{\mathrm {d}}^{\prime \prime}&=&\displaystyle x_{\mathrm {l}}+\frac {1}{\displaystyle \frac {1}{x_{\mathrm {kd}}}+\frac {1}{\displaystyle x_{\mathrm {fd}}}+\frac {1}{x_{\mathrm {ad}}}} \\[ 5pt ] X_{\mathrm {d}}^{\prime }&=&\displaystyle x_{\mathrm {l}}+\frac {1}{\displaystyle \frac {1}{x_{\mathrm {fd}}}+\frac {1}{x_{\mathrm {ad}}}} \\[ 5pt ] \end{eqnarray}
\] であるから，
\[
\begin{eqnarray}
\frac {T_{\mathrm {d}}^{\prime \prime}}{T_{\mathrm {d0}}^{\prime \prime}}&=&\frac {X_{\mathrm {d}}^{\prime \prime}}{X_{\mathrm {d}}^{\prime }} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ヘ
(3)と同様に求めるが，過渡時においては，制動巻線は無視できるので，$ \ r_{\mathrm {fd}} \ $で減衰される時定数は，
\[
\begin{eqnarray}
T_{\mathrm {d0}}^{\prime}&=&\frac { x_{\mathrm {fd}}+x_{\mathrm {ad}}}{2\pi f r_{\mathrm {fd}}} \\[ 5pt ] T_{\mathrm {d}}^{\prime}&=&\frac {\displaystyle x_{\mathrm {fd}}+\frac {1}{\displaystyle \frac {1}{x_{\mathrm {ad}}}+\frac {1}{x_{\mathrm {l}}}}}{2\pi f r_{\mathrm {fd}}} \\[ 5pt ] \end{eqnarray}
\] となるので，その比は，
\[
\begin{eqnarray}
\frac {T_{\mathrm {d}}^{\prime }}{T_{\mathrm {d0}}^{\prime}}&=&\frac {\displaystyle x_{\mathrm {fd}}+\frac {1}{\displaystyle \frac {1}{x_{\mathrm {ad}}}+\frac {1}{x_{\mathrm {l}}}}}{ x_{\mathrm {fd}}+x_{\mathrm {ad}}} \\[ 5pt ] &=&\frac {\displaystyle x_{\mathrm {fd}}(x_{\mathrm {l}}+x_{\mathrm {ad}})+x_{\mathrm {l}}x_{\mathrm {ad}}}{(x_{\mathrm {l}}+x_{\mathrm {ad}})(x_{\mathrm {fd}}+x_{\mathrm {ad}})} \\[ 5pt ] &=&\frac {\displaystyle x_{\mathrm {l}}(x_{\mathrm {fd}}+x_{\mathrm {ad}})+x_{\mathrm {fd}}x_{\mathrm {ad}}}{(x_{\mathrm {l}}+x_{\mathrm {ad}})(x_{\mathrm {fd}}+x_{\mathrm {ad}})} \\[ 5pt ] &=&\frac {\displaystyle x_{\mathrm {l}}+\frac {1}{\frac {1}{x_{\mathrm {fd}}}+\frac {1}{x_{\mathrm {ad}}}}}{ x_{\mathrm {l}}+x_{\mathrm {ad}}} \\[ 5pt ] \end{eqnarray}
\] となる。ワンポイント解説「2.初期過渡リアクタンス$ \ X_{\mathrm {d}}^{\prime \prime} \ $と過渡リアクタンス$ \ X_{\mathrm {d}}^{\prime} \ $，同期リアクタンス$ \ X_{\mathrm {d}} \ $」より，
\[
\begin{eqnarray}
X_{\mathrm {d}}^{\prime }&=&\displaystyle x_{\mathrm {l}}+\frac {1}{\displaystyle \frac {1}{x_{\mathrm {fd}}}+\frac {1}{x_{\mathrm {ad}}}} \\[ 5pt ] X_{\mathrm {d}}&=&\displaystyle x_{\mathrm {l}}+x_{\mathrm {ad}} \\[ 5pt ] \end{eqnarray}
\] であるから，
\[
\begin{eqnarray}
\frac {T_{\mathrm {d}}^{\prime }}{T_{\mathrm {d0}}^{\prime}}&=&\frac {X_{\mathrm {d}}^{\prime}}{X_{\mathrm {d}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。