【問題】
【難易度】★★★☆☆(普通)
次の文章は,誘導機に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。
三相電源に接続した誘導機の固定子巻線は,電源周波数と\( \ \fbox { (1) } \ \)とで決まる同期速度\( \ N_{0} \ \)の回転磁界を発生させる。回転子の回転速度\( \ N \ \)が回転磁界に対して相対速度をもてば,これに応じた誘導電流が回転子巻線に流れ,トルクを発生させる。この相対速度の関係を滑り\( \ \displaystyle s=\frac {N_{0}-N}{N_{0}} \ \)で表す。
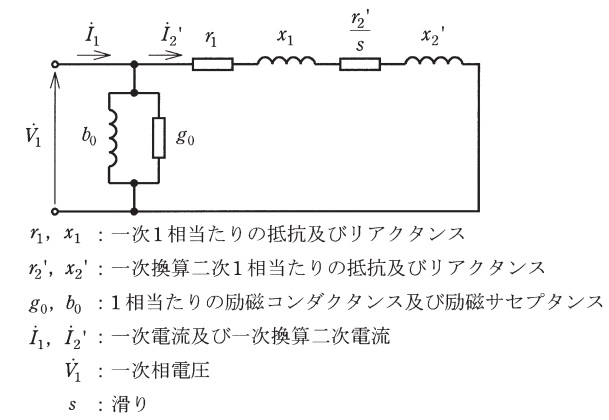
図は,誘導機の\( \ 1 \ \)相分の簡易等価回路である。これから一次相電圧\( \ {\dot V}_{1} \ \)(大きさ\( \ V_{1} \ \))を基準ベクトルとし,励磁電流を考慮して入力複素電力\( \ {\dot W}_{1} \ \)を求めると,
\[
{\dot W}_{1}=P_{1}+\mathrm {j}Q_{1}=3\overline {{\dot V}_{1}}{\dot I}_{1}=3V_{1}^{2}\left[ \fbox { (2) }\right]
\]
となる。ここで,\( \ \displaystyle R=r_{1}+\frac {r_{2}^{\prime }}{s} \ \),\( \ X=x_{1}+x_{2}^{\prime } \ \)とする。電動機が無負荷(軸出力が零)であれば,機械損\( \ P_{\mathrm {m}} \ \)(風損や摩擦損など)と釣り合うトルクを発生すればよいので,\( \ \fbox { (3) } \ =0 \ \)を満たす正の小さい滑りとなり,回転子は同期速度より少し遅い速度で回転する。
この回転子を他の原動機によって駆動して機械損を補償し,さらに同期速度以上の速度で回転磁界の方向に回転させると,発電機運転となり,原動機からの機械的入力に抗して回転子のトルクは回転磁界と逆の方向に働く。すなわち,機械的入力から機械損を引き,さらに励磁損と銅損との和\( \ \fbox { (4) } \ \)を除いたものが電気出力となる。この出力を大きくすると,滑りは\( \ \fbox { (5) } \ \),遅れ無効電力の誘導機での消費が増える。この無効電力は三相電源から供給しなければならないので,同期機のように単独での発電機運転はできない。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& \left( R+\frac {1}{g_{0}}\right) -\mathrm {j}\left( X+\frac {1}{b_{0}}\right) &(ロ)& 3V_{1}^{2}\left( \frac {R}{R^{2}+X^{2}}\right) -P_{\mathrm {m}} \\[ 5pt ]
&(ハ)& 3V_{1}^{2}\left( \frac {\displaystyle \frac {1-s}{s}r_{2}^{\prime }}{R^{2}+X^{2}}+g_{0}\right) &(ニ)& 3V_{1}^{2}\left( \frac {R}{R^{2}+X^{2}}+g_{0}\right) \\[ 5pt ]
&(ホ)& 極 数 &(ヘ)& 導体数 \\[ 5pt ]
&(ト)& 3V_{1}^{2}\left( \frac {\displaystyle \frac {r_{2}^{\prime }}{s}}{R^{2}+X^{2}}\right) -P_{\mathrm {m}} &(チ)& \left( \frac {R}{R^{2}+X^{2}}+g_{0}\right) -\mathrm {j}\left( \frac {X}{R^{2}+X^{2}}+b_{0}\right) \\[ 5pt ]
&(リ)& 変わらず &(ヌ)& \left( \frac {1}{R} +g_{0}\right) -\mathrm {j}\left( \frac {1}{X}+b_{0}\right) \\[ 5pt ]
&(ル)& 3V_{1}^{2}\left( \frac {r_{1}+r_{2}^{\prime }}{R^{2}+X^{2}}+g_{0}\right) &(ヲ)& 負で絶対値が大きくなり \\[ 5pt ]
&(ワ)& 巻 数 &(カ)& 3V_{1}^{2}\left( \frac {\displaystyle \frac {1-s}{s}r_{2}^{\prime }}{R^{2}+X^{2}}\right) -P_{\mathrm {m}} \\[ 5pt ]
&(ヨ)& 正に大きくなり
\end{eqnarray}
\]
【ワンポイント解説】
誘導電動機の問題は二次試験にも頻出の内容となります。二次入力,出力,二次銅損等の導出は確実にできるようにしておきましょう。
1.二次入力,出力,二次銅損の導出及びその関係
問題図において,
①二次入力\( \ P_{2 \ }\)
\[
P_{2}=3\frac {r_{2}^{\prime }}{s}{I_{2}^{\prime }}^{2}
\]
②二次銅損\( \ P_{\mathrm {c2}} \ \)
\[
P_{\mathrm {c2}}=3r_{2}^{\prime }{I_{2}^{\prime }}^{2}
\]
③出力\( \ P_{\mathrm {o}} \ \)
\[
\begin{eqnarray}
P_{\mathrm {o}}&=&P_{2}-P_{\mathrm {c2}} \\[ 5pt ]
&=&3\cdot \frac {1-s}{s}\cdot r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,\(P_{2}:P_{\mathrm {c2}}:P_{\mathrm {o}}=1:s:(1-s)\)となります。
【解答】
(1)解答:ホ
同期速度\( \ N_{0} \ \)は電源周波数を\( \ f \ \),極数を\( \ p \ \)とすると,\( \ \displaystyle N_{0}=\frac {120f}{p} \ \)で求められるので,(ホ)極数が解答となる。
(2)解答:チ
\( \ {\dot W}_{1}=3\overline {{\dot V}_{1}}{\dot I}_{1} \ \)より,本問においては進み無効電力を正としているので,
\[
\begin{eqnarray}
{\dot I}_{1}&=&{\dot V}_{1}\left( g_{0}-\mathrm {j}b_{0}\right) +\frac {{\dot V}_{1}}{R+\mathrm {j}X} \\[ 5pt ]
&=&{\dot V}_{1}\left( g_{0}-\mathrm {j}b_{0}+\frac {R-\mathrm {j}X}{R^{2}+X^{2}}\right) \\[ 5pt ]
&=&{\dot V}_{1}\left \{\left( \frac {R}{R^{2}+X^{2}}+g_{0}\right) -\mathrm {j}\left( \frac {X}{R^{2}+X^{2}}+b_{0}\right) \right\} \\[ 5pt ]
\end{eqnarray}
\]
となるから,
\[
\begin{eqnarray}
{\dot W}_{1}&=&3\overline {{\dot V}_{1}}{\dot I}_{1} \\[ 5pt ]
&=&3V_{1}^{2}\left \{ \left( \frac {R}{R^{2}+X^{2}}+g_{0}\right) -\mathrm {j}\left( \frac {X}{R^{2}+X^{2}}+b_{0}\right) \right\} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:カ
二次電流\( \ {\dot I}_{2}^{\prime } \ \)は,
\[
\begin{eqnarray}
{\dot I}_{2}^{\prime }&=&\frac {{\dot V}_{1}}{R+\mathrm {j}X} \\[ 5pt ]
\end{eqnarray}
\]
となるので,ワンポイント解説「1.二次入力,出力,二次銅損の導出及びその関係」より,電動機出力\( \ P_{\mathrm {o}} \ \)は,二次電流の大きさ\( \ I_{2}^{\prime } \ \)とすると,
\[
\begin{eqnarray}
P_{\mathrm {o}}&=&3\cdot \frac {1-s}{s}\cdot r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ]
&=&3\cdot \frac {1-s}{s}\cdot r_{2}^{\prime }\left| \frac {{\dot V}_{1}}{R+\mathrm {j}X}\right| ^{2} \\[ 5pt ]
&=&3V_{1}^{2}\left( \frac {\displaystyle \frac {1-s}{s}r_{2}^{\prime }}{R^{2}+X^{2}}\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,無負荷の時は\( \ P_{\mathrm {o}}-P_{\mathrm {m}}=0 \ \)となるので,
\[
3V_{1}^{2}\left( \frac {\displaystyle \frac {1-s}{s}r_{2}^{\prime }}{R^{2}+X^{2}}\right) -P_{\mathrm {m}} =0
\]
と求められる。
(4)解答:ル
励磁損\( \ P_{\mathrm {i}} \ \)及び銅損\( \ P_{\mathrm {c}} \ \)の大きさは,
\[
\begin{eqnarray}
P_{\mathrm {i}}&=&3g_{0}V_{1}^{2} \\[ 5pt ]
P_{\mathrm {c}}&=&3\left( r_{1}+r_{2}^{\prime }\right) {I_{2}^{\prime }}^{2} \\[ 5pt ]
&=&3\left( r_{1}+r_{2}^{\prime }\right) \frac {V_{1}^{2}}{R^{2}+X^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,励磁損\( \ P_{\mathrm {i}} \ \)と銅損\( \ P_{\mathrm {c}} \ \)の合計は,
\[
\begin{eqnarray}
P_{\mathrm {i}}+P_{\mathrm {c}}&=&3g_{0}V_{1}^{2}+3\left( r_{1}+r_{2}^{\prime }\right) \frac {V_{1}^{2}}{R^{2}+X^{2}} \\[ 5pt ]
&=&3V_{1}^{2}\left( \frac {r_{1}+r_{2}^{\prime }}{R^{2}+X^{2}}+g_{0}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヲ
発電機運転において滑り\( \ s \ \)は,
\[
s=\frac {N_{0}-N}{N_{0}} < 0
\]
となり,出力を大きくするため回転速度\( \ N \ \)を大きくすると,滑りは負で絶対値が大きくなる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん