《機械》〈情報伝送及び処理〉[R02:問7]プログラム開発のプロジェクト管理に関する空欄穴埋問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★☆☆☆☆（易しい）

次の文章は，プログラム開発のプロジェクト管理に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

プログラム開発のプロジェクト管理方法として，作業展開構造$ \ \left( \mathrm {WBS} \right) \ $を利用する方法がある。これはプロジェクトを構成する作業を分解し，構造化したもので，その作業単位をワークパッケージという。作業展開構造を詳細なレベルとすることで，リスク要因が明らかとなり，コストやスケジュールの予測が可能となる。

作業単位相互の関連性やプロジェクトの流れ，リソースの有効性や外部要因の制約などを考慮した上で，全体のスケジュールを決定する。

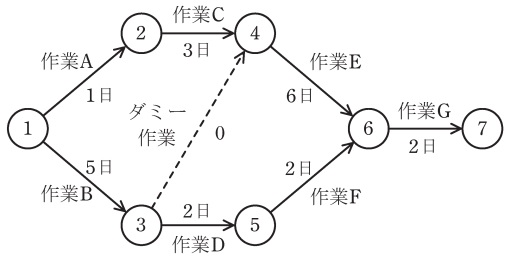
図は，$ \ \fbox {　（１）　} \ $と呼ばれるもので，作業と所要日数をグラフ状に表現したものである。破線はダミー作業で，作業$ \ \mathrm {B} \ $及び作業$ \ \mathrm {C} \ $が完了した後，作業$ \ \mathrm {E} \ $が着手可能であることを示している。ダミー作業の所要日数は$ \ 0 \ $である。

図では，作業$ \ \mathrm {A} \ $と作業$ \ \mathrm {C} \ $に対して作業$ \ \mathrm {B} \ $が並行作業であり，同様に作業$ \ \mathrm {D} \ $と$ \ \fbox {　（２）　} \ $に対して，$ \ \fbox {　（３）　} \ $も並行作業である。

この図では，全体の作業を完了するのに必要な最小限の日数を求めることができ，この経路を$ \ \fbox {　（４）　} \ $という。この図の場合，最小日数は$ \ \fbox {　（５）　} \ $日間である。$ \ \fbox {　（４）　} \ $において遅延が生じると作業全体が遅れることになる。

完了までの日数の予測は，開発の$ \ \fbox {　（６）　} \ $段階であるほど，未知数の要因が多く，難しくなる。

〔問7の解答群〕
\[
\begin{eqnarray}
&（イ）&　13　　　　　&（ロ）&　作業 \ \mathrm {E}　　　　　&（ハ）&　作業 \ \mathrm {G} \\[ 5pt ] &（ニ）&　作業 \ \mathrm {B}　　　　　&（ホ）&　初期　　　　　&（ヘ）&　終期 \\[ 5pt ] &（ト）&　作業 \ \mathrm {A}　　　　　&（チ）&　作業 \ \mathrm {C}　　　　　&（リ）&　クリティカルパス \\[ 5pt ] &（ヌ）&　トラフィック　　　　　&（ル）&　12　　　　　　&（ヲ）&　11 \\[ 5pt ] &（ワ）&　ネットワークモデル　　　　　&（カ）&　作業 \ \mathrm {F}　　　　　&（ヨ）&　ガントチャート \\[ 5pt ] &（タ）&　アローダイアグラム　　　　　　　&（レ）&　ボトルネック　　　　　　&& \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

アローダイアグラムと呼ばれる作業を統括してわかりやすく整理するために用いられるツールに関する問題です。
問題としては一度研修を受けたことがある方であればすぐにわかる易しい問題ですが，電験のテキストには掲載のない内容なので「知っていたらラッキー」な問題です。
製造現場を扱う方であれば実際の工程管理にも使用されたことがある方もいるかもしれません。

1.アローダイアグラムのルール
問題図のように基本的に単純なアローダイアグラムですが，いくつかルールがあります。自分で作ってみるとわかりますが，ルール④や⑤はやりがちになり作成するのに最初は結構苦戦します。
①　作業開始もしく作業完了以外の結合点では必ず前後の結合点と矢印でつながる。
②　結合点の番号や矢印のアルファベットは作業開始から工程の順にそって番号をつける。
③　ある結合点からの作業はその結合点に向かう事前作業が全て完了していなければならない。
④　作業の工程は同じ結合点を二度通るような経路を持ってはいけない。
⑤　並行作業は結合点を増設し，点線矢印でダミー作業を設ける。

アローダイアグラムを作り，作業開始から作業完了までの日数が最も長くなる作業経路をクリティカルパスといい，納期を遵守するためにはこのクリティカルパスを遅らせないことが重要となります。

【解答】

(1)解答：タ
題意より，解答候補は（ワ）ネットワークモデル，（ヨ）ガントチャート，（タ）アローダイアグラム，等になると思います。
問題図のような作業ツールをアローダイアグラムといいます。

(2)解答：カ
(3)解答：ロ
題意より，解答候補は（ロ）作業$ \ \mathrm {E} \ $，（ニ）作業$ \ \mathrm {B} \ $，（ト）作業$ \ \mathrm {A} \ $，（チ）作業$ \ \mathrm {C} \ $，（カ）作業$ \ \mathrm {F} \ $，となると思います。
ワンポイント解説「1.アローダイアグラムのルール」の通り，並行作業は点線矢印で繋がれている結合点を並行している作業なので，作業$ \ \mathrm {D} \ $と作業$ \ \mathrm {F} \ $に対する作業$ \ \mathrm {E} \ $が並行作業となります。

(4)解答：リ
題意より，解答候補は（リ）クリティカルパス，（ヌ）トラフィック，（レ）ボトルネック，等になると思います。
ワンポイント解説「1.アローダイアグラムのルール」の通り，全体の作業を完了するのに必要な最小限の日数の経路をクリティカルパスといいます。似たような用語ですが，ボトルネックは作業工程で一番処理能力が低く弱い部分，トラフィックは通信回線における一定時間に送られるデータ量のことを指します。

(5)解答：イ
題意より，解答候補は（イ）$ \ 13 \ $，（ル）$ \ 12 \ $，（ヲ）$ \ 11 \ $，となると思います。
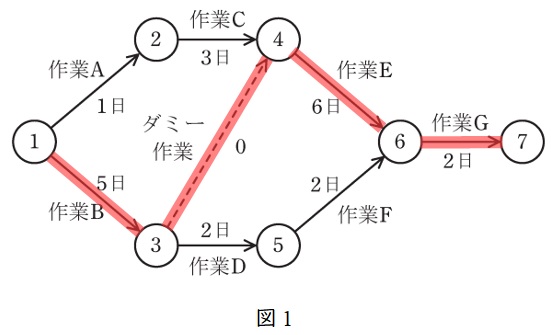
問題図における作業工程が最も長くなるルート，すなわちクリティカルパスは下図のようになり，合計日数は，
\[
\begin{eqnarray}
5+0+6+2 &=&13 \\[ 5pt ] \end{eqnarray}
\] と求められます。