《機械》〈照明〉[R02:問4]円形テーブルの平均照度と照明率の算出に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，円形テーブルの平均照度と照明率の算出の手順を示した記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

照明の省エネルギーを図るために，光源から放射された光を有効に利用すること，すなわち照明率を高めることも重要な要件の一つである。

今，すべての方向に$ \ I=80 \ \mathrm {cd} \ $の光度を有する点光源があり，直径$ \ 1.2 \ \mathrm {m} \ $の円形テーブルの中心直上，高さ$ \ 80 \ \mathrm {cm} \ $の位置に設置してある。テーブルの平均照度と照明率を以下の手順で求める。ただし，平面角$ \ \theta \ $を回転してできる錐体の立体角$ \ \omega \ $は，$ \ \omega =2\pi \left( 1-\cos \theta \right) \ $により求まる。

この点光源の全光束$ \ \mathit {\Phi }_{0} \ $は，すべての方向の光度が$ \ I=80 \ \mathrm {cd} \ $であるので，$ \ \fbox {　（１）　} \ \mathrm {lm} \ $である。また，この点光源からテーブル面に入射する光束$ \ \mathit {\Phi }_{\mathrm {T}} \ $は，点光源からテーブル面を見込む立体角$ \ \omega _{\mathrm {T}} \ $が$ \ \fbox {　（２）　} \ $であるので，$ \ \fbox {　（３）　} \ \mathrm {lm} \ $となる。これよりテーブルの平均照度$ \ E \ $は$ \ \fbox {　（４）　} \ \mathrm {lx} \ $となる。

この点光源の円形テーブルに対する照明率$ \ U \ $は，$ \ \fbox {　（５）　} \ $となる。

円形テーブルへの照明率を高めるには，光源の上部に反射笠などを設置し，周囲に逃げる光束をテーブル面方向に反射させるようにする。

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　0.1　　　　　&（ロ）&　0.2　　　　　&（ハ）&　0.4 \\[ 5pt ] &（ニ）&　0.2\pi　　　　　&（ホ）&　0.4\pi　　　　　&（ヘ）&　0.8\pi \\[ 5pt ] &（ト）&　50　　　　　&（チ）&　84　　　　　&（リ）&　89 \\[ 5pt ] &（ヌ）&　95　　　　　&（ル）&　101　　　　　&（ヲ）&　201 \\[ 5pt ] &（ワ）&　251　　　　　&（カ）&　503　　　　　&（ヨ）&　1005 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

円形テーブルの平均照度と照明率に関する問題で，電験$ \ 2 \ $種や$ \ 3 \ $種でも過去類題を見たことがあるような問題であると思います。
本問は選択肢が絞れないですが基本公式を理解していると解ける問題が多いので，意図的に点数差を広げようとしている出題者の意図が感じられる問題であると思います。

1.立体角の定義
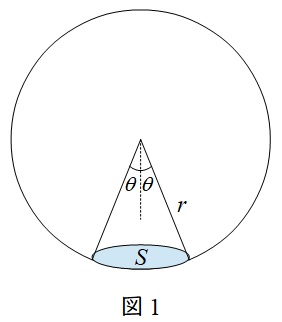
図1のように球体があり，半径$ \ r \ \mathrm {[m]} \ $の錐体が球面を切り取った時の面積を$ \ S \ \mathrm {[m^{2}]} \ $とすると，立体角$ \ \omega \ \mathrm {[sr]} \ $は，
\[
\begin{eqnarray}
\omega &=&\frac {S}{r^{2}} \\[ 5pt ] \end{eqnarray}
\] であり，平面角$ \ \theta \ \mathrm {[rad]} \ $で表すと，
\[
\begin{eqnarray}
\omega &=&2\pi \left( 1-\cos \theta \right) \\[ 5pt ] \end{eqnarray}
\] となります。球全体の立体角は$ \ \theta = \pi \ $であり，$ \ \omega =4\pi \ $となります。

2.光度$ \ I \ $
ある方向に向かう光束$ \ F \ \mathrm {[lm]} \ $を立体角$ \ \omega \ \mathrm {[sr]} \ $で割ったものが光度$ \ I \ \mathrm {[cd]} \ $となります。
\[
\begin{eqnarray}
I &=&\frac {\Delta F}{\Delta \omega } \\[ 5pt ] \end{eqnarray}
\]

3.照度$ \ E \ $
均一に照射された面の明るさで，面積$ \ A \ \mathrm {[m^{2}]} \ $に入射する光束を$ \ F \ \mathrm {[lm]} \ $とすると，
\[
\begin{eqnarray}
E&=&\frac {F}{A} \ [ \mathrm {lx}] \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ヨ
ワンポイント解説「1.立体角の定義」及び「2.光度$ \ I \ $」の通り，この点光源の全光束$ \ \mathit {\Phi }_{0} \ \mathrm {[lm]} \ $は，
\[
\begin{eqnarray}
\mathit {\Phi }_{0} &=&I\omega \\[ 5pt ] &=&80\times 4\pi \\[ 5pt ] &≒&1005.3　→　1005 \ \mathrm {[lm]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ホ
題意に沿って円形テーブルと光源の関係を描くと図2のようになる。

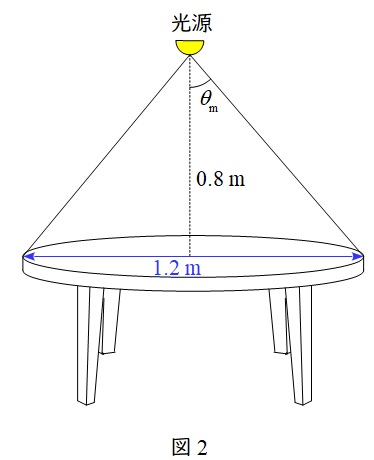
ワンポイント解説「1.立体角の定義」に沿って，図2の立体角$ \ \mathit {\Phi }_{\mathrm {T}} \ $を求める。
図2より光源から円形テーブルの端までの距離$ \ r \ \mathrm {[m]} \ $は，
\[
\begin{eqnarray}
r &=&\sqrt {\left( \frac {1.2}{2}\right) ^{2}+0.8^{2}} \\[ 5pt ] &=&1.0 \ \mathrm {[m]} \\[ 5pt ] \end{eqnarray}
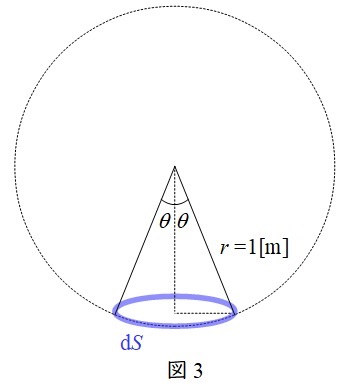
\] となるので，図3に示すような半径$ \ r=1 \ \mathrm {[m]} \ $の球の立体角を求めればよい。
図3に示す微小区間の面積$ \ \mathrm {d}S \ $は，半径$ \ r \sin \theta =\sin \theta \ $の円であるから，
\[
\begin{eqnarray}
\mathrm {d}S &=&2\pi \sin \theta \mathrm {d}\theta \\[ 5pt ] \end{eqnarray}
\] となる。したがって，円形テーブルにおける球面の面積$ \ S \ $は，両辺積分すると，
\[
\begin{eqnarray}
S &=&\int _{0}^{\theta _{\mathrm {m}}}2\pi \sin \theta \mathrm {d}\theta \\[ 5pt ] &=&2\pi \int _{0}^{\theta _{\mathrm {m}}}\sin \theta \mathrm {d}\theta \\[ 5pt ] &=&2\pi \left[ -\cos \theta \right] _{0}^{\theta _{\mathrm {m}}} \\[ 5pt ] &=&2\pi \left( 1-\cos \theta _{\mathrm {m}} \right) \\[ 5pt ] \end{eqnarray}
\] となる。ここで，$ \ \cos \theta _{\mathrm {m}}=\displaystyle \frac {0.8}{1}=0.8 \ $であるから，
\[
\begin{eqnarray}
S &=&2\pi \left( 1-0.8 \right) \\[ 5pt ] &=&0.4\pi \ \mathrm {[m^{2}]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，立体角$ \ \omega _{\mathrm {T}} \ $は，
\[
\begin{eqnarray}
\omega _{\mathrm {T}} &=&\frac {S}{r^{2}} \\[ 5pt ] &=&\frac {0.4\pi }{1.0^{2}} \\[ 5pt ] &=&0.4\pi \ \mathrm {[sr]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

［別解］
題意より，平面角$ \ \theta \ $を回転してできる錐体の立体角$ \ \omega \ $は，$ \ \omega =2\pi \left( 1-\cos \theta \right) \ $で求めることができるので，
\[
\begin{eqnarray}
\omega _{\mathrm {T}} &=&2\pi \left( 1-\cos \theta _{\mathrm {m}} \right) \\[ 5pt ] &=&2\pi \left( 1-0.8 \right) \\[ 5pt ] &=&0.4\pi \ \mathrm {[sr]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ル
テーブル面に入射する光束$ \ \mathit {\Phi }_{\mathrm {T}} \ $は，ワンポイント解説「2.光度$ \ I \ $」より，
\[
\begin{eqnarray}
\mathit {\Phi }_{\mathrm {T}} &=&I\omega _{\mathrm {T}} \\[ 5pt ] &=&80\times 0.4\pi \\[ 5pt ] &≒&100.53　→　101 \ \mathrm {[lm]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：リ
平均照度$ \ E \ $はワンポイント解説「3.照度$ \ E \ $」の通り，光束$ \ \mathit {\Phi }_{\mathrm {T}} \ $をテーブルの面積で割ればよいので，
\[
\begin{eqnarray}
E&=&\frac {\mathit {\Phi }_{\mathrm {T}}}{A} \\[ 5pt ] &=&\frac {100.53}{\pi \times 0.6^{2}} \\[ 5pt ] &≒&88.889　→　89 \ \mathrm {[lx]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：イ
照明率$ \ U \ $は，全光束$ \ \mathit {\Phi }_{0} \ \mathrm {[lm]} \ $に対するテーブル面に入射する光束$ \ \mathit {\Phi }_{\mathrm {T}} \ \mathrm {[lm]} \ $の割合であるから，
\[
\begin{eqnarray}
U&=&\frac {\mathit {\Phi }_{\mathrm {T}}}{\mathit {\Phi }_{0}} \\[ 5pt ] &=&\frac {100.53}{1005.3} \\[ 5pt ] &=&0.1 \\[ 5pt ] \end{eqnarray}
\] と求められる。