【問題】
【難易度】★★★☆☆(普通)
次の文章は,三相同期発電機の試験結果に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
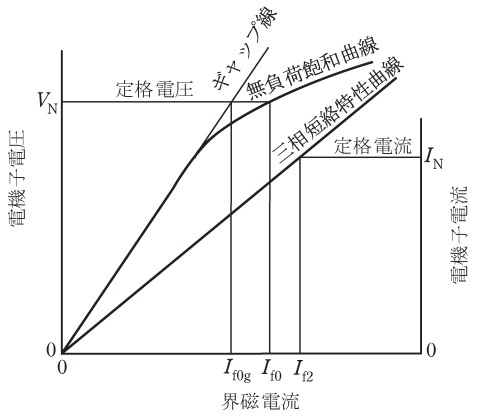
\( \ 16 \ 000 \ \mathrm {kV\cdot A} \ \),\( \ 11 \ 000 \ \mathrm {V} \ \)の定格を持つ三相同期発電機(以下,試験機と呼ぶ)の試験結果は以下のとおりであった。また,試験結果をグラフ化すると図のようになった。
(a) 無負荷飽和特性試験
\[
\begin{array}{|l|r|r|r|r|}
\hline
端子電圧(線間電圧)\ \mathrm {[V]} & 4 \ 000 & 8 \ 000 & 11 \ 000 & 14 \ 300 \\
\hline
界磁電流 \ \mathrm {[A]} & 205 & 410 & 680 & 1 \ 400 \\
\hline
\end{array}
\]
(b) 三相短絡特性試験(定常短絡試験)
\[
\begin{array}{|l|r|r|r|r|}
\hline
電機子電流 \ \mathrm {[A]} & 400 & 600 & 840 \\
\hline
界磁電流 \ \mathrm {[A]} & 435 & 652 & 913 \\
\hline
\end{array}
\]
一般的に同期機には磁気飽和特性があるため,同期リアクタンスには飽和値と不飽和値が定義される。試験機の同期リアクタンスの飽和値\( \ X_{\mathrm {s}} \ \mathrm {[%]} \ \)は,\( \ \fbox { (1) } \ \mathrm {%} \ \)であり,これを\( \ \Omega \ \)値で表した毎相の同期リアクタンスの飽和値\( \ X_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \)は,\( \ \fbox { (2) } \ \mathrm {\Omega } \ \)である。
試験機の同期リアクタンスの不飽和値\( \ X_{\mathrm {su}} \ \mathrm {[%]} \ \)は,図中の記号を用いて\( \ X_{\mathrm {su}} \ \mathrm {[%]}=X_{\mathrm {s}} \ \mathrm {[%]}\times \ \fbox { (3) } \ \)として求められ,試験機の\( \ X_{\mathrm {su}} \ \mathrm {[%]} \ \)は,\( \ \fbox { (4) } \ \mathrm {%} \ \)である。
定格電圧における同期機の磁気飽和の程度を表す飽和率\( \ \sigma \ \)は,図中の記号を用いて,\( \ \displaystyle \sigma = \frac {\fbox { (5) }}{I_{\mathrm {f0g}}} \ \)として求められる。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& 134 &(ロ)& 0.102 &(ハ)& 74.5 \\[ 5pt ]
&(ニ)& 5.63 &(ホ)& 10.2 &(ヘ)& 217 \\[ 5pt ]
&(ト)& 162 &(チ)& 89.8 &(リ)& 1.34 \\[ 5pt ]
&(ヌ)& \left( I_{\mathrm {f2}}-I_{\mathrm {f0g}}\right) &(ル)& \left( I_{\mathrm {f2}}-I_{\mathrm {f0}}\right) &(ヲ)& \left( I_{\mathrm {f0}}-I_{\mathrm {f0g}}\right) \\[ 5pt ]
&(ワ)& \frac {I_{\mathrm {f0}}}{I_{\mathrm {f2}}} &(カ)& \frac {I_{\mathrm {f2}}}{I_{\mathrm {f0g}}} &(ヨ)& \frac {I_{\mathrm {f0}}}{I_{\mathrm {f0g}}} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
同期発電機の無負荷飽和特性曲線と三相短絡特性曲線からの出題です。
\( \ 2 \ \)種では出題されにくい一次試験の計算問題ですが,この問題のように\( \ 1 \ \)種では一次試験から出題されることがあります。
百分率インピーダンスは\( \ 1 \ \)種では使いこなせるレベルまで引き上げる必要があるので,(1)~(4)の計算を確実に理解しておくようにしましょう。
1.オームから百分率インピーダンスへの変換
基準容量を\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \),基準電圧を\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \),基準電流を\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)とすると,\( \ Z \ \mathrm {[\Omega ]} \ \)の百分率インピーダンス\( \ %Z \ \mathrm {[%]} \ \)は,
\[
\begin{eqnarray}
%Z&=&\frac {ZI_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}\times 100 (定義) \\[ 5pt ]
&=&\frac {\sqrt {3}ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ]
&=&\frac {\sqrt {3}ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ]
&=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100 (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
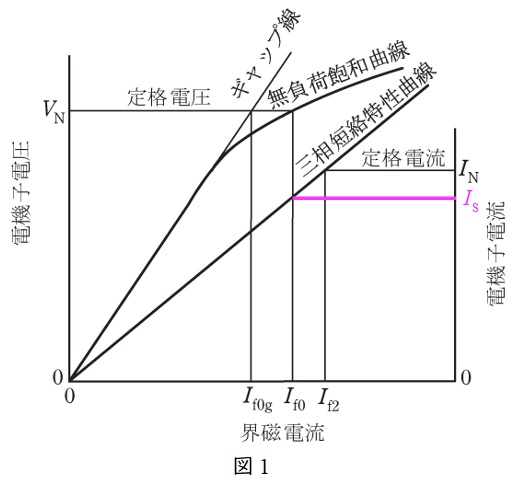
(1)解答:イ
図1の通り,定格電圧\( \ V_{\mathrm {N}} \ \mathrm {[V]} \ \)の時の電機子電流を\( \ I_{\mathrm {S}} \ \mathrm {[A]} \ \)とすると,同期リアクタンスの飽和値\( \ X_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
X_{\mathrm {s}} \ \mathrm {[\Omega ]}&=&\frac {V_{\mathrm {N}}}{\sqrt {3}I_{\mathrm {S}}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,同期リアクタンスの飽和値\( \ X_{\mathrm {s}} \ \mathrm {[%]} \ \)は,ワンポイント解説「1.オームから百分率インピーダンスへの変換」の通り,
\[
\begin{eqnarray}
X_{\mathrm {s}} \ \mathrm {[%]}&=&\frac {P_{\mathrm {N}}X_{\mathrm {s}} \ \mathrm {[\Omega ]}}{V_{\mathrm {N}}^{2}}\times 100 \\[ 5pt ]
&=&\frac {\displaystyle P_{\mathrm {N}}\frac {V_{\mathrm {N}}}{\sqrt {3}I_{\mathrm {S}}}}{V_{\mathrm {N}}^{2}}\times 100 \\[ 5pt ]
&=&\frac { P_{\mathrm {N}}}{\sqrt {3}V_{\mathrm {N}}I_{\mathrm {S}}}\times 100 \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,(a)無負荷飽和特性試験より,定格電圧\( \ V_{\mathrm {N}}=11 \ 000 \ \mathrm {[V]} \ \)のときの界磁電流\( \ I_{\mathrm {f0}}=680 \ \mathrm {[A]} \ \)であるから,(b)三相短絡特性試験より,\( \ I_{\mathrm {S}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {S}}&=&\frac {600}{652}\times 680 \\[ 5pt ]
&≒&625.77 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ X_{\mathrm {s}} \ \mathrm {[%]} \ \)は,
\[
\begin{eqnarray}
X_{\mathrm {s}} \ \mathrm {[%]}&=&\frac { P_{\mathrm {N}}}{\sqrt {3}V_{\mathrm {N}}I_{\mathrm {S}}}\times 100 \\[ 5pt ]
&=&\frac {16 \ 000 \times 10^{3}}{\sqrt {3}\times 11 \ 000\times 625.77}\times 100 \\[ 5pt ]
&≒&134.20 → 134 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ホ
ワンポイント解説「1.オームから百分率インピーダンスへの変換」より,
\[
\begin{eqnarray}
X_{\mathrm {s}} \ \mathrm {[%]}&=&\frac {P_{\mathrm {N}}X_{\mathrm {s}} \ \mathrm {[\Omega ]}}{V_{\mathrm {N}}^{2}}\times 100 \\[ 5pt ]
X_{\mathrm {s}} \ \mathrm {[\Omega ]}&=&\frac {X_{\mathrm {s}} \ \mathrm {[%]}V_{\mathrm {N}}^{2}}{100P_{\mathrm {N}}} \\[ 5pt ]
\end{eqnarray}
\]
であるから,各値を代入すると,
\[
\begin{eqnarray}
X_{\mathrm {s}} \ \mathrm {[\Omega ]}&=&\frac {134.20\times 11 \ 000^{2}}{100\times 16 \ 000 \times 10^{3}} \\[ 5pt ]
&≒&10.149 → 10.1 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
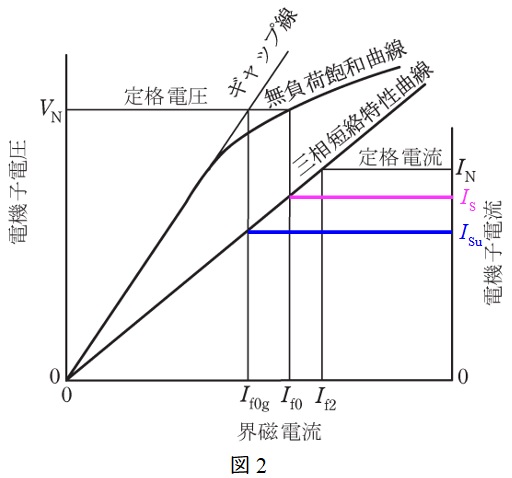
(3)解答:ヨ
(1)と同様に考えると,図2において\( \ X_{\mathrm {su}} \ \mathrm {[%]} \ \)は,
\[
\begin{eqnarray}
X_{\mathrm {su}} \ \mathrm {[%]}&=&\frac { P_{\mathrm {N}}}{\sqrt {3}V_{\mathrm {N}}I_{\mathrm {Su}}}\times 100 \\[ 5pt ]
&=&\frac { P_{\mathrm {N}}}{\displaystyle \sqrt {3}V_{\mathrm {N}}\frac {I_{\mathrm {f0g}}}{I_{\mathrm {f0}}}I_{\mathrm {S}}}\times 100 \\[ 5pt ]
&=&\frac { P_{\mathrm {N}}}{\sqrt {3}V_{\mathrm {N}}I_{\mathrm {S}}}\times 100 \times \frac {I_{\mathrm {f0}}}{I_{\mathrm {f0g}}} \\[ 5pt ]
&=&X_{\mathrm {s}} \ \mathrm {[%]} \times \frac {I_{\mathrm {f0}}}{I_{\mathrm {f0g}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ト
(a)無負荷飽和特性試験より,\( \ I_{\mathrm {f0g}} \ \mathrm {[A]} \ \)の大きさは,
\[
\begin{eqnarray}
I_{\mathrm {f0g}}&=&\frac {11 \ 000}{4 \ 000}\times 205 \\[ 5pt ]
&=&563.75 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,(3)解答式より,
\[
\begin{eqnarray}
X_{\mathrm {su}} \ \mathrm {[%]}&=&X_{\mathrm {s}} \ \mathrm {[%]} \times \frac {I_{\mathrm {f0}}}{I_{\mathrm {f0g}}} \\[ 5pt ]
&=&134.20 \times \frac {680}{563.75} \\[ 5pt ]
&≒&161.87 → 162 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヲ
磁気飽和の程度を表す飽和率\( \ \sigma \ \)は,\( \ I_{\mathrm {f0g}} \ \mathrm {[A]} \ \)を基準としたときの\( \ I_{\mathrm {f0}} \ \mathrm {[A]} \ \)の飽和率であるから,
\[
\begin{eqnarray}
\sigma &=&\frac {I_{\mathrm {f0}}-I_{\mathrm {f0g}}}{I_{\mathrm {f0g}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん