《機械》〈照明〉[R07:問4]光束法を用いた室内照明設計に関する計算・空欄穴埋問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，光束法を用いた室内照明設計に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

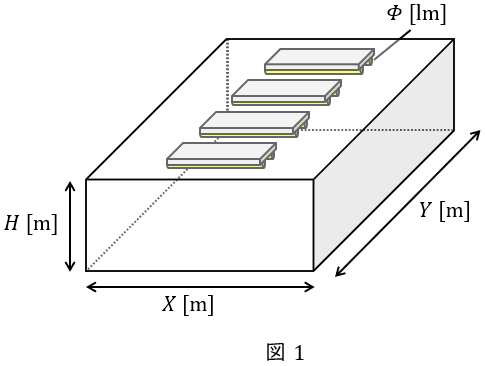
全般照明方式によって事務室の照明を行う。使用する光源は直管形$ \ \mathrm {LED} \ $ランプを用いた照明器具で，同一機種のもの複数台を規則的に天井に配置する。光束法を適用して必要な照明器具の台数を求めたい。設計諸元は以下のとおりである。

事務室の間口：$ \ X= 18 \ \mathrm {m} \ $
事務室の奥行：$ \ Y= 6 \ \mathrm {m} \ $
天井高さ（床面から）：$ \ Z= 3.05 \ \mathrm {m} \ $
照明器具：天井埋込形　直管形$ \ \mathrm {LED} \ $ランプ$ \ 1 \ $灯用$ \ N \ $台
　　　　　ランプ$ \ 1 \ $灯の定格光束　$ \ \mathit {\Phi }=3 \ 800 \ \mathrm {lm} \ $
光源の高さ（床面から）　：$ \ H= 3.05 \ \mathrm {m} \ =Z \ $
作業面の高さ（床面から）：$ \ h= 0.8 \ \mathrm {m} \ $
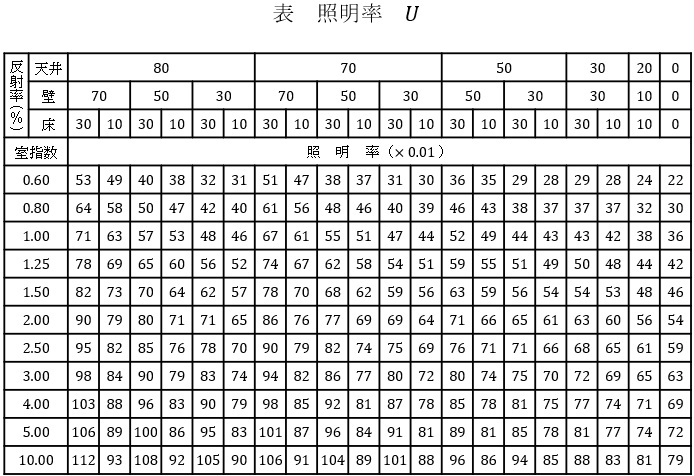
室内面の反射率：天井$ \ 70 \ \mathrm {％} \ $，壁$ \ 50 \ \mathrm {％} \ $，床$ \ 10 \ \mathrm {％} \ $

$ \ \fbox {　（１）　} \ $：$ \ M=0.81 \ $
　$ \ \fbox {　（１）　} \ $$ \ M \ $は新設時の平均照度に対する，ある一定期間使用した後の平均照度の比である。使用しているうちにランプは光束がしだいに減少し，照明器具は汚れによって器具効率が低下するため，設計の際に光束にあらかじめ余裕をもたせておくための係数である。

照明率：$ \ U \ $
　照明率$ \ U \ $は光源の光束が作業面に届く割合であり，照明器具の配光，器具効率，室の寸法，作業面から光源までの高さ，室内面の反射率によって決まる係数である。具体的には，①式から室指数$ \ K_{\mathrm {r}} \ $の値を求め，照明器具の製造者によって提供される照明率表からその値を得る。
\[
\begin{eqnarray}
K_{\mathrm {r}} &=& \ \fbox {　（２）　} \ ······························　① \\[ 5pt ] \end{eqnarray}
\] ここでの照明率$ \ U \ $の値は，上記諸元ならびに下記の照明率表から，$ \ \fbox {　（３）　} \ $となる。

作業面の設計照度：$ \ E \ \mathrm {[lx]} \ $
　作業面の設計照度$ \ E \ $は作業面の水平面照度の室内全体の平均値であり，②式で表される。
\[
\begin{eqnarray}
E &=& \ \fbox {　（４）　} \ ·······························　② \\[ 5pt ] \end{eqnarray}
\] 以上から，作業面の設計照度$ \ E \ $を$ \ 750 \ \mathrm {lx} \ $に設定した場合，最小限必要となる照明器具の台数$ \ N \ $は$ \ \fbox {　（５）　} \ $台であることが求まる。

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {\mathit {\Phi } NM}{UXY}　　　　　&（ロ）&　\frac {\left( X+Y\right) H}{XY}　　　　　&（ハ）&　\frac {\mathit {\Phi } NUM}{XY} \\[ 5pt ] &（ニ）&　0.40　　　　　&（ホ）&　0.62　　　　　&（ヘ）&　0.69 \\[ 5pt ] &（ト）&　20　　　　　&（チ）&　26　　　　　&（リ）&　39 \\[ 5pt ] &（ヌ）&　\frac {XY}{\left( X+Y\right) H}　　　　　　　&（ル）&　\frac {\mathit {\Phi } NU}{MXY}　　　　　&（ヲ）&　\frac {XY}{\left( X+Y\right) \left( H-h\right) } \\[ 5pt ] &（ワ）&　保守率　　　　　&（カ）&　光束維持率　　　　　　　&（ヨ）&　光束余裕率 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

光束法を用いた室内照明設計に関する問題です。
室指数を用いるところが高度な問題となっていますが，平成30年問6でも類題が出題されていたので，過去問を学習されていた方は高得点が得られたかと思います。
$ \ 1 \ $種においても過去問学習は非常に有効ですので，多くの過去問に取り組むようにして下さい。

1.光束法による平均照度$ \ E \ $の計算
間口$ \ X \ \mathrm {[m]} \ $，奥行$ \ Y \ \mathrm {[m]} \ $の部屋において，光源１個あたりの光束を$ \ \mathit {\Phi} \ \mathrm {[lm]} \ $，光源の個数を$ \ N \ \mathrm {[個]} \ $とすると，空間内の全光束$ \ F \ \mathrm {[lm]} \ $は，
\[
\begin{eqnarray}
F&=&\mathit {\Phi}N \\[ 5pt ] \end{eqnarray}
\] となり，照明率（光源の光束が作業面に届く割合）を$ \ U \ $，保守率（新設時の平均照度を$ \ 1 \ $としたときの一定期間使用した後の平均照度）を$ \ M \ $とすると，照射面積は$ \ XY \ \mathrm {[m^{2}]} \ $なので，平均照度$ \ E \ \mathrm {[lx]} \ $は，
\[
\begin{eqnarray}
E&=&\frac {FUM}{XY} \\[ 5pt ] &=&\frac {\mathit {\Phi} NUM}{XY} \\[ 5pt ] \end{eqnarray}
\] で求められます。

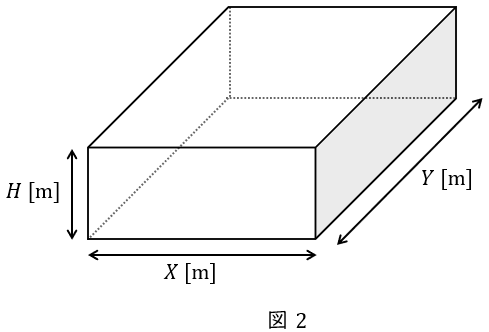
2.室指数
室指数$ \ K \ $は照明率$ \ U \ $を求めるための指数で，壁面の面積に対する床面の面積の割合であり図2においては，
\[
\begin{eqnarray}
K&=&\frac {XY}{H\left( X+Y\right) } \\[ 5pt ] \end{eqnarray}
\] で求められます。ただし，机上等床面からの高さがある場合を想定する際は作業面の高さを$ \ H \ $から差し引く必要があります。

【解答】

(1)解答：ワ
題意より解答候補は，（ワ）保守率，（カ）光束維持率，（ヨ）光束余裕率，になると思います。
ワンポイント解説「1.光束法による平均照度$ \ E \ $の計算」の通り，新設時の平均照度に対する，ある一定期間使用した後の平均照度の比を保守率といいます。

(2)解答：ヲ
題意より解答候補は，（ロ）$ \ \displaystyle \frac {\left( X+Y\right) H}{XY} \ $，（ヌ）$ \ \displaystyle \frac {XY}{\left( X+Y\right) H} \ $，（ヲ）$ \ \displaystyle \frac {XY}{\left( X+Y\right) \left( H-h\right) } \ $，になると思います。
ワンポイント解説「2.室指数」の通り，本問における室指数は$ \ \displaystyle K_{\mathrm {r}}=\frac {XY}{\left( X+Y\right) \left( H-h\right) } \ $となります。

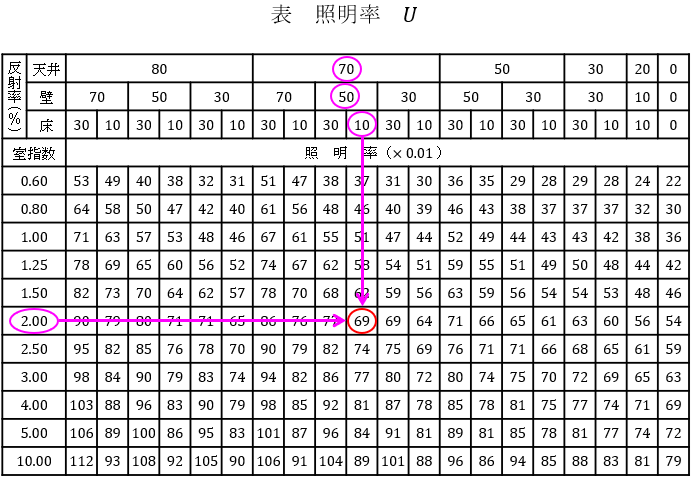
(3)解答：ヘ
(2)解答式に各値を代入すると室指数$ \ K_{\mathrm {r}} \ $は，
\[
\begin{eqnarray}
K_{\mathrm {r}}&=&\frac {XY}{\left( X+Y\right) \left( H-h\right) } \\[ 5pt ] &=&\frac {18\times 6}{\left( 18+6\right) \times \left( 3.05-0.8\right) } \\[ 5pt ] &=&2.00 \\[ 5pt ] \end{eqnarray}
\] となるので，照明率表より，照明率$ \ U=0.69 \ $と求められる。

(4)解答：ハ
題意より解答候補は，（イ）$ \ \displaystyle \frac {\mathit {\Phi } NM}{UXY} \ $，（ハ）$ \ \displaystyle \frac {\mathit {\Phi } NUM}{XY} \ $，（ル）$ \ \displaystyle \frac {\mathit {\Phi } NU}{MXY} \ $，になると思います。
ワンポイント解説「1.光束法による平均照度$ \ E \ $の計算」の通り，作業面の設計照度は，$ \ E= \displaystyle \frac {\mathit {\Phi } NUM}{XY} \ $となります。

(5)解答：リ
(4)解答式に各値を代入すると，
\[
\begin{eqnarray}
E&=&\frac {\mathit {\Phi} NUM}{XY} \\[ 5pt ] 750&=&\frac {3 \ 800 N\times 0.69\times 0.81}{18\times 6} \\[ 5pt ] N&=&\frac {750\times 18\times 6}{3 \ 800 \times 0.69\times 0.81} \\[ 5pt ] &≒&38.13　→　39 \\[ 5pt ] \end{eqnarray}
\] と求められる。