【問題】
【難易度】★★★☆☆(普通)
定格出力\( \ 50 \ \mathrm {[kV\cdot A]} \ \),定格一次電圧\( \ 6 \ 300 \ \mathrm {[V]} \ \),定格二次電圧\( \ 210 \ \mathrm {[V]} \ \),定格周波数\( \ 60 \ \mathrm {[Hz]} \ \),巻線の材質が銅である単相変圧器がある。この変圧器の高圧側を開放して低圧側に周波数\( \ 60 \ \mathrm {[Hz]} \ \),電圧\( \ 210 \ \mathrm {[V]} \ \)を加えて無負荷試験をしたところ,電力計の指示が\( \ 137 \ \mathrm {[W]} \ \)であった。次に,低圧側を短絡し,高圧側に定格周波数の電圧\( \ 58 \ \mathrm {[V]} \ \)を加えると定格電流が流れ,そのときの電力計の指示が\( \ 298 \ \mathrm {[W]} \ \)であった。また,巻線の抵抗を測定したところ,一次巻線の抵抗は\( \ 1.18 \ \mathrm {[\Omega ]} \ \),二次巻線の抵抗は\( \ 0.003 \ 8 \ \mathrm {[\Omega ]} \ \)であった。これらの試験温度はいずれも\( \ 25 \ \mathrm {[℃]} \ \)であった。
この変圧器を定格出力,定格電圧,全負荷,負荷力率\( \ 0.8 \ \)(遅れ)で運転したとき,基準温度を\( \ 75 \ \mathrm {[℃]} \ \)として,次の値を求めよ。
(1) 一次換算漏れリアクタンス \( \ \mathrm {[\Omega ]} \ \)
(2) 負荷損 \( \ \mathrm {[W]} \ \)
ただし,基準温度\( \ 75 \ \mathrm {[℃]} \ \)における負荷損\( \ P_{75} \ \mathrm {[W]} \ \)は,温度\( \ t \ \mathrm {[℃]} \ \)における負荷損を\( \ P_{Lt} \ \mathrm {[W]} \ \),銅損を\( \ P_{ct} \ \mathrm {[W]} \ \)とすれば,次式で表される。
\[
\begin{eqnarray}
P_{75} &=& P_{ct}\left( \frac {310}{235+t}\right) +\left( P_{Lt}-P_{ct}\right) \left( \frac {235+t}{310}\right) \\[ 5pt ]
\end{eqnarray}
\]
(3) 効率 \( \ \mathrm {[%]} \ \)
(4) 電圧変動率 \( \ \mathrm {[%]} \ \)
ただし,電圧変動率の計算には簡略式を用いてもよい。
【ワンポイント解説】
変圧器の無負荷試験と短絡試験から効率と電圧変動率を求める問題です。
基準温度を\( \ 75 \ \mathrm {[℃]} \ \)としたり,負荷損と銅損を区別したりしているところが高等な内容となっています。
問題文をよく読んでどの部分を求める必要があるか考えて解いていくように下さい。
1.変圧器の\( \ \mathrm {L} \ \)形等価回路(一次換算)
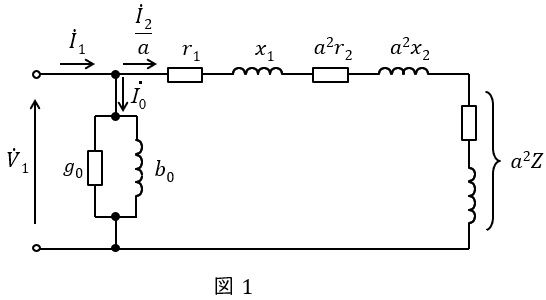
変圧器の一次換算等価回路を図1に示します。ただし,\( \ {\dot V}_{1} \ \mathrm {[V]} \ \)は一次側端子電圧,\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は一次電流,\( \ {\dot I}_{2} \ \mathrm {[A]} \ \)は二次電流,\( \ {\dot I}_{0} \ \mathrm {[A]} \ \)は励磁電流,\( \ r_{1} \ \mathrm {[\Omega ]} \ \)は一次巻線抵抗,\( \ r_{2} \ \mathrm {[\Omega ]} \ \)は二次巻線抵抗,\( \ x_{1} \ \mathrm {[\Omega ]} \ \)は一次漏れリアクタンス,\( \ x_{2} \ \mathrm {[\Omega ]} \ \)は二次漏れリアクタンス,\( \ a \ \)は変圧比(巻数比)となります。
2.変圧器の効率\( \ \eta \ \)と最大効率\( \ \eta _{\mathrm {m}} \ \)
変圧器の損失は鉄損\( \ p_{\mathrm {i}} \ \mathrm {[W]} \ \)と銅損\( \ p_{\mathrm {c}} \ \mathrm {[W]} \ \)があり,\( \ p_{\mathrm {i}} \ \mathrm {[W]} \ \)は負荷によらず一定であり,\( \ p_{\mathrm {c}} \ \mathrm {[W]} \ \)は負荷(電流)の\( \ 2 \ \)乗に比例します。従って,定格出力\( \ P_{\mathrm {n}} \ \mathrm {[W]} \ \)で利用率\( \ \alpha \ \)の時の変圧器の効率\( \ \eta \ \)は,
\[
\begin{eqnarray}
\eta &=&\frac {出力}{入力} \\[ 5pt ]
&=&\frac {出力}{出力+損失} \\[ 5pt ]
&=&\frac {\alpha P_{\mathrm {n}}}{\alpha P_{\mathrm {n}}+p_{\mathrm {i}}+\alpha ^{2}p_{\mathrm {c}}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
次に,最大効率\( \ \eta _{\mathrm {m}} \ \)を求めます。上式の分母分子を\( \ \alpha \ \)で割ると
\[
\begin{eqnarray}
\eta &=&\frac {P_{\mathrm {n}}}{\displaystyle P_{\mathrm {n}}+\frac {p_{\mathrm {i}}}{\alpha }+\alpha p_{\mathrm {c}}} \\[ 5pt ]
\end{eqnarray}
\]
となり,効率が最大となるためには,上式の分母が最小となれば良いです。よって,\( \ \displaystyle A=P_{\mathrm {n}}+\frac {p_{\mathrm {i}}}{\alpha }+\alpha p_{\mathrm {c}} \ \)と置くと,
\[
\begin{eqnarray}
\frac {\mathrm {d}A}{\mathrm {d}\alpha }&=&-\frac {p_{\mathrm {i}}}{\alpha ^{2} }+p_{\mathrm {c}} \\[ 5pt ]
\end{eqnarray}
\]
となります。よって\( \ \displaystyle \frac {\mathrm {d}A}{\mathrm {d}\alpha }=0 \ \)となるとき,\( \ p_{\mathrm {i}}=\alpha ^{2}p_{\mathrm {c}} \ \)であり,鉄損と銅損が等しい時効率は最大となります。
3.無負荷試験の等価回路
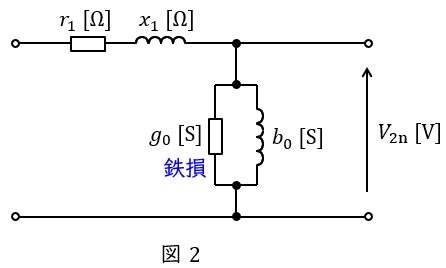
変圧器の無負荷試験は一次側を開放して,二次側に定格電圧を加える試験です。測定される電力は鉄損となり,測定される電力と電流から,励磁コンダクタンス\( \ g_{0} \ \mathrm {[S]} \ \)及び励磁サセプタンス\( \ b_{0} \ \mathrm {[S]} \ \)を求めることが可能となります。二次側に定格電圧を加えるのが一般的ですが,二次側開放で一次側に定格電圧を加えても同様に求められます。
4.短絡試験の等価回路
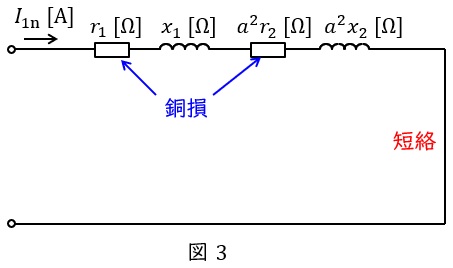
変圧器の短絡試験は二次側を短絡して,一次側にインピーダンス電圧を加えて,定格電流を流す試験です。励磁回路に流れる電流が十分に小さいと仮定すると,測定される電力は負荷損(銅損)となります。測定される電力と電流から,高圧側換算の巻線抵抗\( \ R=r_{1}+a^{2}r_{2} \ \mathrm {[\Omega ]} \ \)及び漏れリアクタンス\( \ X=x_{1}+a^{2}x_{2} \ \mathrm {[\Omega ]} \ \)を求めることが可能となります。
5.オーム法から百分率インピーダンス法への変換
基準容量を\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \),基準電圧を\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \),基準電流を\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)とすると,\( \ Z \ \mathrm {[\Omega ]} \ \)の百分率インピーダンス(パーセントインピーダンス)\( \ %Z \ \mathrm {[%]} \ \)は,
\[
\begin{eqnarray}
%Z&=&\frac {ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 (定義) \\[ 5pt ]
&=&\frac {ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ]
&=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100 (∵P_{\mathrm {n}}=V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ]
\end{eqnarray}
\]
となります。
6.百分率抵抗降下\( \ p \ \)と百分率リアクタンス降下\( \ q \ \)
変圧器の一次二次を合算した二次側換算の抵抗成分を\( \ R=\displaystyle \frac {r_{1}}{a^{2}}+r_{2} \ \),一次二次を合算した二次側換算のリアクタンス成分を\( \ X=\displaystyle \frac {x_{1}}{a^{2}}+x_{2} \ \)とし,定格二次電圧を\( \ V_{\mathrm {2n}} \ \mathrm {[V]} \ \),定格二次電流を\( \ I_{\mathrm {2n}} \ \mathrm {[A]} \ \)とすると,百分率抵抗降下\( \ p \ \mathrm {[%]} \ \)及び百分率リアクタンス降下\( \ q \ \mathrm {[%]} \ \)は,
\[
\begin{eqnarray}
p &=&\frac {RI_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 \ \mathrm {[%]} \\[ 5pt ]
q &=&\frac {XI_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
となります。
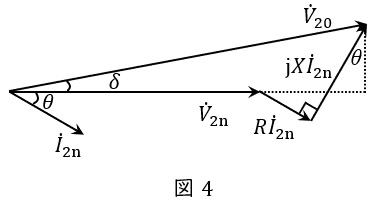
定格負荷(遅れ力率\( \ \cos \theta \ \))を接続したときの変圧器のベクトル図は図4のように描くことができ,電圧変動率\( \ \varepsilon \ \)は上記\( \ p \ \),\( \ q \ \)を用いると,
\[
\begin{eqnarray}
\varepsilon &=&\frac {V_{20}-V_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 \\[ 5pt ]
&≃&p\cos \theta + q\sin \theta +\frac {1}{200}\left( q\cos \theta -p\sin \theta \right) ^{2} \\[ 5pt ]
\end{eqnarray}
\]
と近似することができ,\( \ {\dot V}_{\mathrm {20}} \ \)と\( \ {\dot V}_{\mathrm {2n}} \ \)の位相差が十分に小さく,\( \ \varepsilon \ \)が\( \ 4 % \ \)以下の場合には,
\[
\begin{eqnarray}
\varepsilon &≃&p\cos \theta + q\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
と近似することができます。
【解答】
(1)一次換算漏れリアクタンス \( \ \mathrm {[\Omega ]} \ \)
定格出力\( \ S_{n}=50 \ \mathrm {[kV\cdot A]} \ \),定格一次電圧\( \ V_{1n}=6 \ 300 \ \mathrm {[V]} \ \)より定格一次電流\( \ I_{1n} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{1n} &=&\frac {S_{n}}{V_{1n}} \\[ 5pt ]
&=&\frac {50\times 10^{3}}{6 \ 300} \\[ 5pt ]
&≒&7.936 \ 5 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
であり,題意より短絡試験時にはこの大きさの電流が流れる。ワンポイント解説「4.短絡試験の等価回路」の通り,短絡試験時には励磁回路の電流は十分に小さいと考えれば良いので,短絡試験時の電力計の指示\( \ P_{s}=298 \ \mathrm {[W]} \ \)より,一次換算全巻線抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
P_{s} &=& RI_{1n}^{2} \\[ 5pt ]
R&=&\frac {P_{s}}{I_{1n}^{2}} \\[ 5pt ]
&=&\frac {298}{7.936 \ 5^{2}} \\[ 5pt ]
&≒&4.731 \ 1 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となる。また,短絡試験時の一次電圧\( \ V_{1s}=58 \ \mathrm {[V]} \ \)より,一次二次の合成したインピーダンス\( \ Z \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
Z &=&\frac {V_{1s}}{I_{1n}} \\[ 5pt ]
&=&\frac {58}{7.936 \ 5} \\[ 5pt ]
&≒&7.308 \ 0 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,一次換算全漏れリアクタンス\( \ X \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
X &=&\sqrt {Z^{2}-R^{2}} \\[ 5pt ]
&=&\sqrt {7.308 \ 0^{2}-4.731 \ 1^{2}} \\[ 5pt ]
&≒&5.569 \ 9 → 5.57 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)負荷損 \( \ \mathrm {[W]} \ \)
題意より,本問における\( \ 25 \ \mathrm {[℃]} \ \)における負荷損\( \ P_{L25} \ \mathrm {[W]} \ \)は短絡試験時の電力計の指示\( \ P_{s}=298 \ \mathrm {[W]} \ \)と等しい。また,一次巻線の抵抗\( \ r_{1}=1.18 \ \mathrm {[\Omega ]} \ \),二次巻線の抵抗\( \ r_{2}=0.003 \ 8 \ \mathrm {[\Omega ]} \ \)より,\( \ 25 \ \mathrm {[℃]} \ \)における銅損\( \ P_{c25} \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P_{c25} &=&\left\{ r_{1}+\left( \frac {V_{1n}}{V_{2n}}\right) ^{2}r_{2}\right\} {I_{1n}}^{2} \\[ 5pt ]
&=&\left\{ 1.18+\left( \frac {6 \ 300}{210}\right) ^{2}\times 0.003 \ 8 \right\} \times 7.936 \ 5^{2} \\[ 5pt ]
&≒&289.75 \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,与式より\( \ 75 \ \mathrm {[℃]} \ \)における負荷損\( \ P_{75} \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P_{75} &=& P_{c25}\left( \frac {310}{235+25}\right) +\left( P_{L25}-P_{c25}\right) \left( \frac {235+25}{310}\right) \\[ 5pt ]
&=& 289.75\times \left( \frac {310}{235+25}\right) +\left( 298-289.75\right) \times \left( \frac {235+25}{310}\right) \\[ 5pt ]
&≒& 352.39 → 352 \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)効率 \( \ \mathrm {[%]} \ \)
無負荷試験の結果より,鉄損\( \ P_{i}=137 \ \mathrm {[W]} \ \)であり温度により変化はないとみなせるので,基準温度\( \ 75 \ \mathrm {[℃]} \ \),力率\( \ \cos \theta =0.8 \ \)の定格運転時における効率\( \ \eta _{75} \ \mathrm {[%]} \ \)は,ワンポイント解説「2.変圧器の効率\( \ \eta \ \)と最大効率\( \ \eta _{\mathrm {m}} \ \)」の通り,
\[
\begin{eqnarray}
\eta _{75} &=& \frac {S_{n}\cos \theta }{S_{n}\cos \theta +P_{i}+P_{75}}\times 100 \\[ 5pt ]
&=& \frac {50\times 10^{3}\times 0.8 }{50\times 10^{3}\times 0.8 +137+352.39}\times 100 \\[ 5pt ]
&≒& 98.791 → 98.8 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)電圧変動率 \( \ \mathrm {[%]} \ \)
百分率抵抗降下\( \ p \ \mathrm {[%]} \ \),百分率リアクタンス降下\( \ q \ \mathrm {[%]} \ \)及び\( \ \sin \theta \ \)は,ワンポイント解説「6.百分率抵抗降下\( \ p \ \)と百分率リアクタンス降下\( \ q \ \)」の通り,
\[
\begin{eqnarray}
p &=&\frac {R_{75}I_{1n}}{V_{1n}}\times 100 \\[ 5pt ]
&=&\frac {R_{75}{I_{1n}}^{2}}{V_{1n}I_{1n}}\times 100 \\[ 5pt ]
&=&\frac {P_{75}}{S_{n}}\times 100 \\[ 5pt ]
&=&\frac {352.39 }{50\times 10^{3}}\times 100 \\[ 5pt ]
&≒&0.704 \ 78 \ \mathrm {[%]} \\[ 5pt ]
q &=&\frac {XI_{\mathrm {1n}}}{V_{\mathrm {1n}}}\times 100 \\[ 5pt ]
&=&\frac {5.569 \ 9\times 7.936 \ 5 }{6 \ 300}\times 100 \\[ 5pt ]
&≒&0.701 \ 67 \ \mathrm {[%]} \\[ 5pt ]
\sin \theta &=&\sqrt {1-\cos ^{2}\theta } \\[ 5pt ]
&=&\sqrt {1-0.8 ^{2} } \\[ 5pt ]
&=&0.6 \\[ 5pt ]
\end{eqnarray}
\]
となるので,電圧変動率\( \ \varepsilon \ \mathrm {[%]} \ \)は,ワンポイント解説「6.百分率抵抗降下\( \ p \ \)と百分率リアクタンス降下\( \ q \ \)」の通り,
\[
\begin{eqnarray}
\varepsilon &≃&p\cos \theta + q\sin \theta \\[ 5pt ]
&=&0.704 \ 78\times 0.8 + 0.701 \ 67\times 0.6 \\[ 5pt ]
&≒&0.985 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん