【問題】
【難易度】★★★☆☆(普通)
定格電圧,定格周波数のもとで運転している三相巻線形誘導電動機がある。本問で考慮する運転範囲では,負荷の要求するトルクは\( \ T=k_{0}+k_{1}n^{2} \ \)で表される。ただし,\( \ k_{0} \ \),\( \ k_{1} \ \)は定数であり,また,\( \ T \ \)は同期ワットで表したトルク(誘導電動機の二次入力に相当)を誘導電動機の定格容量で除した値で,単位法で表したトルクである。\( \ n \ \)は回転速度を同期速度で除した値である。次の問に答えよ。
(1) 滑りを\( \ s \ \)として,\( \ n \ \)を\( \ s \ \)で表す式を求めよ。また,単位法で表した出力及びトルクを\( \ P \ \mathrm {[p.u.]} \ \)及び\( \ T \ \mathrm {[p.u.]} \ \)とするとき,\( \ T \ \)を\( \ s \ \)及び\( \ P \ \)で表す式を求めよ。
(2)a.スリップリング間に外部抵抗を挿入して\( \ 1 \ \)相当たりの二次抵抗の値を\( \ r_{21} \ \)としたところ,電動機の出力\( \ P_{1} \ \)が\( \ 0.6 \ \mathrm {[p.u.]} \ \),滑り\( \ s_{1} \ \)が\( \ 0.1 \ \)となった。このときのトルク\( \ T_{1} \ \mathrm {[p.u.]} \ \)を求めよ。
b.外部抵抗を調節し,出力を\( \ P_{2} \ \mathrm {[p.u.]} \ \)にした。このときの滑りを\( \ s_{2} \ \)及びトルクを\( \ T_{2} \ \mathrm {[p.u.]} \ \)とするとき,\( \ T_{2}-T_{1} \ \)を\( \ k_{1} \ \),\( \ s_{1} \ \)及び\( \ s_{2} \ \)で表す式を求めよ。
c.\( \ P_{2}=0.85 \ \mathrm {[p.u.]} \ \)とするとき,\( \ s_{2} \ \)及び\( \ T_{2} \ \mathrm {[p.u.]} \ \)はいくらか。ただし,\( \ k_{1}=1.64 \ \)であり,また,\( \ \left| x \right| ≪1 \ \)のとき\( \ \left( 1-x\right) ^{3}≒1-3x \ \)と近似できる。
(3)上記(2)で出力\( \ P_{2} \ \)を\( \ 0.85 \ \mathrm {[p.u.]} \ \)としたときの\( \ 1 \ \)相当たりの二次抵抗を\( \ r_{22} \ \)とする。\( \ r_{21} \ \)は\( \ r_{22} \ \)の何倍か。ただし,電動機のトルクと滑りの関係は直線で表されるものとする。
【ワンポイント解説】
誘導電動機の特性に関する出題です。
単位法を使用したり,問題文内で記号を指定したりと,少し戸惑うかもしれませんが,それほど難解な公式は使用しないので,きちんと読解して解けるようにしましょう。
1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)
三相誘導電動機の極数が\( \ p \ \),電源の周波数が\( \ f \ \)の時,同期速度\( \ N_{\mathrm {s}} \ \)は
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.誘導機の滑り\( \ s \ \)
誘導機の同期速度が\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \),回転数が\( \ N \ \mathrm {[{min}^{-1}]} \ \)である時,誘導機の滑り\( \ s \ \)は,
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
となり,上式を変形すると,
\[
\begin{eqnarray}
sN_{\mathrm {s}} &=&N_{\mathrm {s}}-N \\[ 5pt ]
N &=&N_{\mathrm {s}}-sN_{\mathrm {s}} \\[ 5pt ]
&=&N_{\mathrm {s}}\left( 1-s\right) \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係
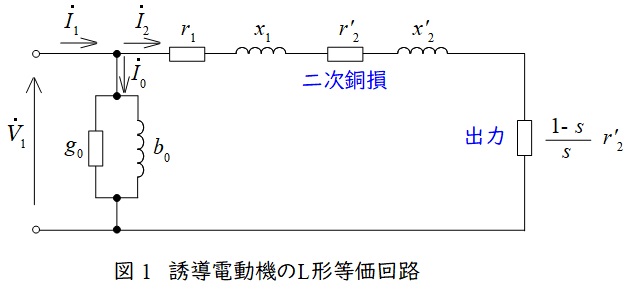
誘導電動機の\( \ \mathrm {L} \ \)形等価回路は図1のようになります。図1において,\( \ {\dot V}_{1} \ \)は一次側端子電圧,\( \ {\dot I}_{1} \ \)は一次電流,\( \ {\dot I}_{2} \ \)は二次電流,\( \ {\dot I}_{0} \ \)は励磁電流,\( \ r_{1} \ \)は一次巻線抵抗,\( \ r_{2}^{\prime } \ \)は二次巻線抵抗の一次換算,\( \ x_{1} \ \)は一次漏れリアクタンス,\( \ x_{2}^{\prime } \ \)は二次漏れリアクタンスの一次換算,\( \ s \ \)は滑りとなります。
図1より,出力\( \ P_{\mathrm {o}} \ \),二次銅損\( \ P_{\mathrm {c2}} \ \),二次入力\( \ P_{2} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {o}} &=& \frac {1-s}{s}r_{2}^{\prime }I_{2}^{2} \\[ 5pt ]
P_{\mathrm {c2}} &=& r_{2}^{\prime }I_{2}^{2} \\[ 5pt ]
P_{2} &=& P_{\mathrm {o}}+P_{\mathrm {c2}} =\frac {r_{2}^{\prime }}{s}I_{2}^{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,誘導電動機の二次入力\( \ P_{2} \ \),出力\( \ P_{\mathrm {o}} \ \),二次銅損\( \ P_{\mathrm {c2}} \ \)には,
\[
\begin{eqnarray}
P_{2}:P_{\mathrm {o}}:P_{\mathrm {c2}} &=& 1:(1-s):s \\[ 5pt ]
\end{eqnarray}
\]
の関係があることが分かります。
4.トルクの比例推移
図1より,三相誘導電動機のトルク\( \ T \ \)は,
\[
\begin{eqnarray}
T &=&\frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ]
&=&\frac {P_{\mathrm {2}}\left( 1-s\right) }{\omega _{\mathrm {s}}\left( 1-s\right) } \\[ 5pt ]
&=&\frac {P_{\mathrm {2}}}{\omega _{\mathrm {s}}} \\[ 5pt ]
&=& \frac {1}{\omega _{\mathrm {s}}}\frac {3V_{1}^{2}\displaystyle \frac {r_{2}^{\prime }}{s}}{\left( r_{1}+\displaystyle \frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
で求められ,\( \ 1≫s \ \)の時,\( \ r_{2}^{\prime } \ \)以外の抵抗やリアクタンスは無視できるので,
\[
\begin{eqnarray}
T &≃& \frac {3V_{1}^{2}s}{\omega _{\mathrm {s}}r_{2}^{\prime }} \\[ 5pt ]
\end{eqnarray}
\]
となり,トルクに対する変数は二次抵抗\( \ r_{2}^{\prime } \ \)と滑り\( \ s \ \)のみであり,トルク\( \ T \ \)を一定とすると,
\[
\begin{eqnarray}
\frac {r_{2}^{\prime }}{s} &=& 一定 \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
【解答】
(1)\( \ n \ \)を\( \ s \ \)で表す式及び\( \ T \ \)を\( \ s \ \)及び\( \ P \ \)で表す式
題意より,回転速度を\( \ N \ \),同期速度を\( \ N_{\mathrm {s}} \ \)とすると,
\[
\begin{eqnarray}
n &=& \frac {N}{N_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
であり,ワンポイント解説「2.誘導機の滑り\( \ s \ \)」より,\( \ N=N_{\mathrm {s}}\left( 1-s\right) \ \)であるから,
\[
\begin{eqnarray}
n &=& \frac {N_{\mathrm {s}}\left( 1-s\right) }{N_{\mathrm {s}}} \\[ 5pt ]
&=& 1-s \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
また,\( \ T \ \)は二次入力に相当し,\( \ P \ \)は出力であるから,ワンポイント解説「3.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係」の通り,
\[
\begin{eqnarray}
\frac {P}{T} &=& \frac {1-s}{1} \\[ 5pt ]
&=& 1-s \\[ 5pt ]
T &=& \frac {P}{1-s} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)a.電動機の出力\( \ P_{1} \ \)が\( \ 0.6 \ \mathrm {[p.u.]} \ \),滑り\( \ s_{1} \ \)が\( \ 0.1 \ \)となったときのトルク\( \ T_{1} \ \mathrm {[p.u.]} \ \)
(1)の解答式に\( \ P_{1} = 0.6 \ \mathrm {[p.u.]} \ \),滑り\( \ s_{1} = 0.1 \ \)を代入すると\( \ T_{1} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
T_{1} &=& \frac {P_{1}}{1-s_{1}} \\[ 5pt ]
&=& \frac {0.6}{1-0.1} \\[ 5pt ]
&≒& 0.66667 → 0.667 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)b.\( \ T_{2}-T_{1} \ \)を\( \ k_{1} \ \),\( \ s_{1} \ \)及び\( \ s_{2} \ \)で表す式
題意より,\( \ T=k_{0}+k_{1}n^{2} \ \)で表されるので,
\[
\begin{eqnarray}
T_{1} &=& k_{0}+k_{1}n_{1}^{2} \\[ 5pt ]
&=& k_{0}+k_{1}\left( 1-s_{1}\right) ^{2} \\[ 5pt ]
T_{2} &=& k_{0}+k_{1}n_{2}^{2} \\[ 5pt ]
&=& k_{0}+k_{1}\left( 1-s_{2}\right) ^{2} \\[ 5pt ]
\end{eqnarray}
\]
となるから,
\[
\begin{eqnarray}
T_{2}-T_{1} &=& k_{0}+k_{1}\left( 1-s_{2}\right) ^{2}-\left\{ k_{0}+k_{1}\left( 1-s_{1}\right) ^{2}\right\} \\[ 5pt ]
&=& k_{1}\left( 1-s_{2}\right) ^{2}-k_{1}\left( 1-s_{1}\right) ^{2} \\[ 5pt ]
&=& k_{1}\left\{ \left( 1-s_{2}\right) ^{2}-\left( 1-s_{1}\right) ^{2}\right\} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)c.\( \ P_{2}=0.85 \ \mathrm {[p.u.]} \ \)とするとき,\( \ s_{2} \ \)及び\( \ T_{2} \ \mathrm {[p.u.]} \ \)の値
\( \ T_{2}=\displaystyle \frac {P_{2}}{1-s_{2}} \ \)であるから,これを(2)b.解答式に代入し整理すると,
\[
\begin{eqnarray}
\frac {P_{2}}{1-s_{2}}-T_{1} &=& k_{1}\left\{ \left( 1-s_{2}\right) ^{2}-\left( 1-s_{1}\right) ^{2}\right\} \\[ 5pt ]
P_{2}-T_{1}\left( 1-s_{2}\right) &=& k_{1}\left\{ \left( 1-s_{2}\right) ^{3}-\left( 1-s_{1}\right) ^{2}\left( 1-s_{2}\right) \right\} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,近似式\( \ \left( 1-x\right) ^{3}≒1-3x \ \)を適用すると,
\[
\begin{eqnarray}
P_{2}-T_{1}\left( 1-s_{2}\right) &≃& k_{1}\left\{ 1-3s_{2}-\left( 1-s_{1}\right) ^{2}\left( 1-s_{2}\right) \right\} \\[ 5pt ]
P_{2}-T_{1}+T_{1}s_{2} &=& k_{1}\left\{ 1-3s_{2}-\left( 1-2s_{1}+s_{1}^{2}\right) \left( 1-s_{2}\right) \right\} \\[ 5pt ]
&=& k_{1}\left\{ \left( 2s_{1}-s_{1}^{2}\right) +\left( -2-2s_{1}+s_{1}^{2}\right)s_{2} \right\} \\[ 5pt ]
\left\{ k_{1}\left( 2+2s_{1}-s_{1}^{2}\right) +T_{1}\right\} s_{2}&=& k_{1}\left( 2s_{1}-s_{1}^{2}\right) -P_{2}+T_{1} \\[ 5pt ]
s_{2}&=& \frac {k_{1}\left( 2s_{1}-s_{1}^{2}\right) -P_{2}+T_{1}}{k_{1}\left( 2+2s_{1}-s_{1}^{2}\right) +T_{1}} \\[ 5pt ]
\end{eqnarray}
\]
と整理できるので,各値を代入すると,
\[
\begin{eqnarray}
s_{2}&=& \frac {1.64\times \left( 2\times 0.1-0.1^{2}\right) -0.85+0.66667}{1.64\times \left( 2+2\times 0.1-0.1^{2}\right) +0.66667} \\[ 5pt ]
&≒&0.030123 → 0.0301 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,\( \ T_{2} \ \)は,
\[
\begin{eqnarray}
T_{2} &=&\frac {P_{2}}{1-s_{2}} \\[ 5pt ]
&=& \frac {0.85}{1-0.030123} \\[ 5pt ]
&≒&0.87640 → 0.876 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)出力\( \ P_{2} \ \)を\( \ 0.85 \ \mathrm {[p.u.]} \ \)としたときの\( \ 1 \ \)相当たりの二次抵抗を\( \ r_{22} \ \)とするとき,\( \ r_{21} \ \)は\( \ r_{22} \ \)の何倍か
ワンポイント解説「4.トルクの比例推移」の通り,
\[
\begin{eqnarray}
T &≃& \frac {3V_{1}^{2}s}{\omega _{\mathrm {s}}r_{2}^{\prime }} \\[ 5pt ]
\end{eqnarray}
\]
の関係があるので,上式を変形すると,
\[
\begin{eqnarray}
\frac {Tr_{2}^{\prime }}{s} &=& 一定 \\[ 5pt ]
\frac {Tr_{2}}{s} &=& 一定 \\[ 5pt ]
\end{eqnarray}
\]
の関係があることが分かる。したがって,
\[
\begin{eqnarray}
\frac {T_{1}r_{21}}{s_{1}} &=& \frac {T_{2}r_{22}}{s_{2}} \\[ 5pt ]
\frac {r_{21}}{r_{22}} &=& \frac {T_{2}}{s_{2}}\cdot \frac {s_{1}}{T_{1}} \\[ 5pt ]
&=& \frac {0.87640}{0.030123}\times \frac {0.1}{0.66667} \\[ 5pt ]
&≒&4.3641 → 4.36 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん