【問題】
【難易度】★★★☆☆(普通)
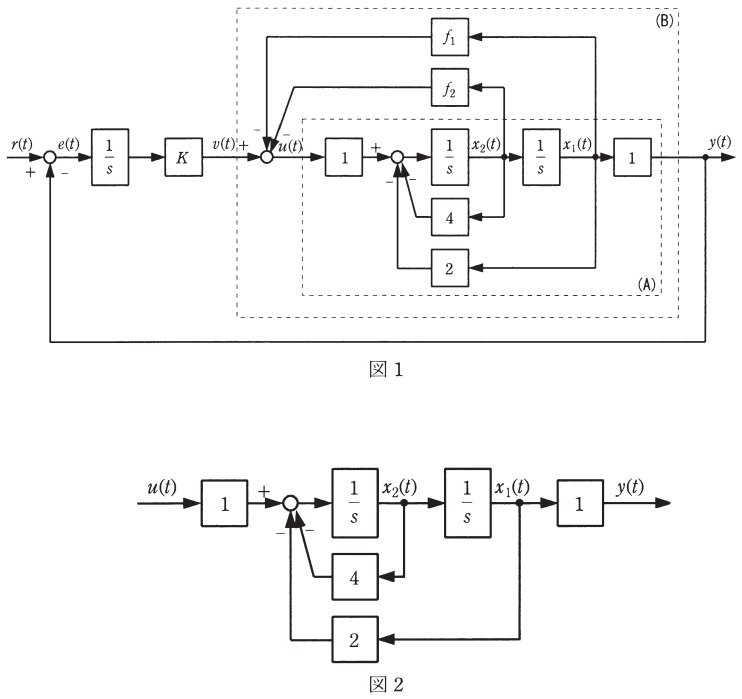
図1のフィードバック制御系において,\( \ r(t) \ \)は目標値,\( \ e(t) \ \)は偏差,\( \ v(t) \ \)は入力,\( \ u(t) \ \)は制御入力,\( \ x_{1}(t) \ \),\( \ x_{2}(t) \ \)は状態,\( \ y(t) \ \)は出力を表す。また,ゲイン\( \ K \ \)は正,上付添字\( \ \mathrm {T} \ \)は転置を表し,\( \ \boldsymbol I \ \)は単位行列を表す。このとき,次の問に答えよ。
(1) 図1のブロック(\( \ \mathrm {A} \ \))だけを取り出した図2の制御対象において,制御入力\( \ u(t) \ \),状態ベクトル\( \ {\boldsymbol x}(t)=\left[ x_{1}(t),x_{2}(t)\right] \ ^{\mathrm {T}} \ \),出力\( \ y(t) \ \)とする。このとき,状態空間表現(\( \ \boldsymbol A \ \),\( \ \boldsymbol b \ \),\( \ {\boldsymbol c}^{\mathrm {T}} \ \))
\[
\begin{eqnarray}
\dot {\boldsymbol x} (t)&=& \boldsymbol A \boldsymbol x (t) +\boldsymbol b u (t) & ・・・・・・・・・①& \\[ 5pt ]
y(t)&=& \boldsymbol c^{\mathrm {T}} \boldsymbol x (t) & ・・・・・・・・・②& \\[ 5pt ]
\end{eqnarray}
\]
における,\( \ \boldsymbol A \ \),\( \ \boldsymbol b \ \),\( \ {\boldsymbol c}^{\mathrm {T}} \ \)を求めよ。さらに,この制御対象が可制御,可観測であることを示せ。
(2) ブロック(\( \ \mathrm {B} \ \))において,制御入力\( \ u(t) \ \)を次の状態フィードバック
\[
\begin{eqnarray}
u(t)&=& -\boldsymbol f^{\mathrm {T}} \boldsymbol x (t) +v (t)=-f_{1}x_{1}(t)-f_{2}x_{2}(t)+v (t) & ・・・・・・・・・③& \\[ 5pt ]
\end{eqnarray}
\]
によって与えている。ここで,\( \ \boldsymbol f^{\mathrm {T}}=\left[ f_{1},f_{2}\right] \ \)とおいた。③式を①式に代入した状態空間表現(\( \ \boldsymbol A-\boldsymbol b \boldsymbol f^{\mathrm {T}} \ \),\( \ \boldsymbol b \ \),\( \ {\boldsymbol c}^{\mathrm {T}} \ \))における\( \ \boldsymbol A-\boldsymbol b \boldsymbol f^{\mathrm {T}} \ \)を求め,特性多項式\( \ \det \left[ s\boldsymbol I-\left( \boldsymbol A-\boldsymbol b \boldsymbol f^{\mathrm {T}}\right) \right] \ \)を\( \ f_{1} \ \),\( \ f_{2} \ \)を用いて表せ。さらに,特性根を\( \ -5±\mathrm {j}10 \ \)に配置するための\( \ f_{1} \ \),\( \ f_{2} \ \)を求めよ。
(3) 上記(2)で求めた\( \ f_{1} \ \),\( \ f_{2} \ \)のとき,入力\( \ v(t) \ \)から出力\( \ y(t) \ \)までのブロック(\( \ \mathrm {B} \ \))の伝達関数\( \ G_{\mathrm {f}}(s) \ \)を求めよ。ただし,計算式\( \ G_{\mathrm {f}}(s)={\boldsymbol c}^{\mathrm {T}}\left[ s\boldsymbol I-\left( \boldsymbol A-\boldsymbol b \boldsymbol f^{\mathrm {T}}\right) \right]^{-1}\boldsymbol b \ \),又はブロック線図の変形を利用してよい。
(4) 上記(2)で求めた\( \ f_{1} \ \),\( \ f_{2} \ \)のとき,図1のフィードバック制御系全体の安定限界における三つの閉ループ極を求めよ。
【ワンポイント解説】
近年は現代制御理論に関する問題が圧倒的に多くなってきています。本問は解くのに少し時間がかかりますが,自動制御の問題としては標準かやや易しめな問題で基本的な内容を理解するには非常に良い問題と言えると思います。
1.行列の可制御性
\[
\begin{eqnarray}
\dot {\boldsymbol x} (t) &=&\boldsymbol A\boldsymbol x\left( t\right)+\boldsymbol b u\left( t\right) \\[ 5pt ]
\end{eqnarray}
\]
が与えられているとき,可制御性行列\( \ \boldsymbol U_{\mathrm {c}}=\begin{pmatrix} \boldsymbol b & \boldsymbol A \boldsymbol b \end{pmatrix}\)の\(\mathrm {rank} \ \boldsymbol U_{\mathrm {c}}=2 \ \)または\( \ \det \boldsymbol U_{\mathrm {c}}≠0 \ \)の時,可制御となります。
2.行列の可観測性
\[
\begin{eqnarray}
\dot {\boldsymbol x} (t) &=&\boldsymbol A\boldsymbol x\left( t\right)+\boldsymbol b u\left( t\right) \\[ 5pt ]
y(t)&=& \boldsymbol c^{\mathrm {T}} \boldsymbol x (t) \\[ 5pt ]
\end{eqnarray}
\]
が与えられているとき,可観測性行列\( \ \boldsymbol U_{\mathrm {o}}=\begin{pmatrix} \boldsymbol c^{\mathrm {T}} \\ \boldsymbol c^{\mathrm {T}} \boldsymbol A \end{pmatrix}\)の\(\mathrm {rank} \ \boldsymbol U_{\mathrm {o}}=2 \ \)または\( \ \det \boldsymbol U_{\mathrm {o}}≠0 \ \)の時,可観測となります。
3.ラウスの安定判別法
特性方程式\(a_{0}s^{n}+a_{1}s^{n-1}+a_{2}s^{n-2}+\cdots +a_{n-1}s+a_{n}=0\)が与えられている時,ラウスの安定判別法による安定条件は,
\[
\begin{eqnarray}
&&1. s^{3},s^{2},s^{1},s^{0}の係数がすべて存在 \\[ 5pt ]
&&2. s^{3},s^{2},s^{1},s^{0}の係数がすべて同符号 \\[ 5pt ]
&&3. ラウスの数表の値がすべて正であること \\[ 5pt ]
\end{eqnarray}
\]
です。ラウスの数表は下記図のようになります。
\[
\begin{array}{c|ccc}
& 1列 & 2列 & 3列 \\
\hline
1行 & a_{0} & a_{2} & a_{4} & \cdots \\
2行 & a_{1} & a_{3} & a_{5} & \cdots \\
3行 & b_{1}=\frac {a_{1}a_{2}-a_{0}a_{3}}{a_{1}} & b_{2}=\frac {a_{1}a_{4}-a_{0}a_{5}}{a_{1}} & \cdots \\
4行 & c_{1}=\frac {b_{1}a_{3}-a_{1}b_{2}}{b_{1}} & c_{2}=\frac {b_{1}a_{5}-a_{1}b_{3}}{b_{1}} & \cdots \\
\vdots & \vdots & \vdots &
\end{array}
\]
【解答】
(1)\( \ \boldsymbol A \ \),\( \ \boldsymbol b \ \),\( \ {\boldsymbol c}^{\mathrm {T}} \ \)を求める
図2より,
\[
\begin{eqnarray}
X_{1}(s) &=&\frac {1}{s}X_{2}(s) &⇔& sX_{1}(s)=X_{2}(s) \\[ 5pt ]
X_{2}(s)&=&\frac {1}{s}\left\{ -2X_{1}(s)-4X_{2}(s)+U(s) \right\} &⇔& sX_{2}(s)=-2X_{1}(s)-4X_{2}(s)+U(s) \\[ 5pt ]
Y(s)&=&X_{1}(s) && \\[ 5pt ]
\end{eqnarray}
\]
が成り立つので,両辺をラプラス逆変換すると,
\[
\begin{eqnarray}
{\dot x}_{1}(t) &=&x_{2}(t) \\[ 5pt ]
{\dot x}_{2}(t) &=&-2x_{1}(t)-4x_{2}(t)+u(t) \\[ 5pt ]
y(t)&=&x_{1}(t) \\[ 5pt ]
\end{eqnarray}
\]
となり,状態空間表現をすると,
\[
\begin{eqnarray}
\begin{bmatrix} \dot x_{1}(t) \\ \dot x_{2}(t) \end{bmatrix}&=&\begin{bmatrix} 0 & 1 \\ -2 & -4 \end{bmatrix}\begin{bmatrix} x_{1}(t) \\ x_{2}(t) \end{bmatrix}+\begin{bmatrix} 0 \\ 1 \end{bmatrix}u(t) \\[ 5pt ]
y(t) &=&\begin{bmatrix} 1 & 0 \end{bmatrix}\begin{bmatrix} x_{1}(t) \\ x_{2}(t) \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
\displaystyle \boldsymbol A=\begin{bmatrix} 0 & 1 \\ -2 & -4 \end{bmatrix},\displaystyle \boldsymbol b=\begin{bmatrix} 0 \\ 1 \end{bmatrix},\displaystyle \boldsymbol c^{\mathrm {T}}=\begin{bmatrix} 1 & 0 \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。ワンポイント解説「1.行列の可制御性」より,
\[
\begin{eqnarray}
\begin{pmatrix} \boldsymbol b & \boldsymbol A \boldsymbol b \end{pmatrix}&=&\begin{bmatrix} 0 & 1 \\ 1 & -4 \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
であり,
\[
\begin{eqnarray}
\det \left[ \begin{pmatrix} \boldsymbol b & \boldsymbol A \boldsymbol b \end{pmatrix}\right] &=&\det \begin{bmatrix} 0 & 1 \\ 1 & -4 \end{bmatrix} \\[ 5pt ]
&=&-1≠0 \\[ 5pt ]
\end{eqnarray}
\]
であるため,可制御である。また,ワンポイント解説「2.行列の可観測性」より,
\[
\begin{eqnarray}
\begin{pmatrix} \boldsymbol c^{\mathrm {T}} \\ \boldsymbol c^{\mathrm {T}} \boldsymbol A \end{pmatrix}&=&\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
であり,
\[
\begin{eqnarray}
\det \left[ \begin{pmatrix} \boldsymbol c^{\mathrm {T}} \\ \boldsymbol c^{\mathrm {T}} \boldsymbol A \end{pmatrix}\right] &=&\det \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \\[ 5pt ]
&=&1≠0 \\[ 5pt ]
\end{eqnarray}
\]
であるため,可観測である。
(2)\( \ \boldsymbol A-\boldsymbol b \boldsymbol f^{\mathrm {T}} \ \)を求め,特性多項式\( \ \det \left[ s\boldsymbol I-\left( \boldsymbol A-\boldsymbol b \boldsymbol f^{\mathrm {T}}\right) \right] \ \)を\( \ f_{1} \ \),\( \ f_{2} \ \)を用いて表す。さらに,特性根を\( \ -5±\mathrm {j}10 \ \)に配置するための\( \ f_{1} \ \),\( \ f_{2} \ \)を求める
③を①に代入すると,
\[
\begin{eqnarray}
\dot {\boldsymbol x} (t)&=& \boldsymbol A \boldsymbol x (t) +\boldsymbol b u (t) \\[ 5pt ]
&=& \boldsymbol A \boldsymbol x (t) +\boldsymbol b \left\{ -\boldsymbol f^{\mathrm {T}} \boldsymbol x (t) +v (t)\right\} \\[ 5pt ]
&=& \left( \boldsymbol A -\boldsymbol b \boldsymbol f^{\mathrm {T}}\right) \boldsymbol x (t) +\boldsymbol bv (t) \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\( \ \boldsymbol A-\boldsymbol b \boldsymbol f^{\mathrm {T}} \ \)は,
\[
\begin{eqnarray}
\boldsymbol A-\boldsymbol b \boldsymbol f^{\mathrm {T}}&=& \begin{bmatrix} 0 & 1 \\ -2 & -4 \end{bmatrix}-\begin{bmatrix} 0 \\ 1 \end{bmatrix}\begin{bmatrix} f_{1} & f_{2} \end{bmatrix} \\[ 5pt ]
&=& \begin{bmatrix} 0 & 1 \\ -2 & -4 \end{bmatrix}-\begin{bmatrix} 0 & 0 \\ f_{1} & f_{2} \end{bmatrix} \\[ 5pt ]
&=& \begin{bmatrix} 0 & 1 \\ -2-f_{1} & -4-f_{2} \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。特性多項式は,
\[
\begin{eqnarray}
\det \left[ s\boldsymbol I-\left( \boldsymbol A-\boldsymbol b \boldsymbol f^{\mathrm {T}}\right) \right] &=&0 \\[ 5pt ]
\det \left[ \begin{bmatrix} s & 0 \\ 0 & s \end{bmatrix}-\begin{bmatrix} 0 & 1 \\ -2-f_{1} & -4-f_{2} \end{bmatrix}\right] &=&0 \\[ 5pt ]
\det \begin{bmatrix} s & -1 \\ 2+f_{1} & s+4+f_{2} \end{bmatrix} &=&0 \\[ 5pt ]
s\left( s+4+f_{2}\right) -\left( -1\right) \left( 2+f_{1}\right) &=&0 \\[ 5pt ]
s^{2}+\left( 4+f_{2}\right) s+\left( 2+f_{1}\right) &=&0 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。\( \ -5±\mathrm {j}10 \ \)に配置するためには,
\[
\begin{eqnarray}
\left( s+5+\mathrm {j}10\right) \left( s+5-\mathrm {j}10\right) &=&0 \\[ 5pt ]
\end{eqnarray}
\]
が成り立たなければならないので,左辺を展開すると,
\[
\begin{eqnarray}
s^{2}+10s +125 &=&0 \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,係数比較すると,
\[
\begin{eqnarray}
4+f_{2} &=&10 ⇔ f_{2}=6 \\[ 5pt ]
2+f_{1} &=&125 ⇔ f_{1}=123 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)入力\( \ v(t) \ \)から出力\( \ y(t) \ \)までのブロック(\( \ \mathrm {B} \ \))の伝達関数\( \ G_{\mathrm {f}}(s) \ \)
\( \ \left[ s\boldsymbol I-\left( \boldsymbol A-\boldsymbol b \boldsymbol f^{\mathrm {T}}\right) \right] ^{-1} \ \)は,
\[
\begin{eqnarray}
\left[ s\boldsymbol I-\left( \boldsymbol A-\boldsymbol b \boldsymbol f^{\mathrm {T}}\right) \right] ^{-1} &=&\begin{bmatrix} s & -1 \\ 125 & s+10 \end{bmatrix} ^{-1} \\[ 5pt ]
&=&\frac {1}{s\left( s+10\right) +125}\begin{bmatrix} s+10 & 1 \\ -125 & s \end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
であり,題意より\( \ G_{\mathrm {f}}(s)={\boldsymbol c}^{\mathrm {T}}\left[ s\boldsymbol I-\left( \boldsymbol A-\boldsymbol b \boldsymbol f^{\mathrm {T}}\right) \right]^{-1}\boldsymbol b \ \)であるので,
\[
\begin{eqnarray}
G_{\mathrm {f}}(s) &=&{\boldsymbol c}^{\mathrm {T}}\left[ s\boldsymbol I-\left( \boldsymbol A-\boldsymbol b \boldsymbol f^{\mathrm {T}}\right) \right]^{-1}\boldsymbol b \\[ 5pt ]
&=&\begin{bmatrix} 1 & 0 \end{bmatrix}\frac {1}{s\left( s+10\right) +125}\begin{bmatrix} s+10 & 1 \\ -125 & s \end{bmatrix}\begin{bmatrix} 0 \\ 1 \end{bmatrix} \\[ 5pt ]
&=&\frac {1}{s\left( s+10\right) +125}\begin{bmatrix} 1 & 0 \end{bmatrix}\begin{bmatrix} s+10 & 1 \\ -125 & s \end{bmatrix}\begin{bmatrix} 0 \\ 1 \end{bmatrix} \\[ 5pt ]
&=&\frac {1}{s^{2}+10s+125}\begin{bmatrix} s+10 & 1 \end{bmatrix}\begin{bmatrix} 0 \\ 1 \end{bmatrix} \\[ 5pt ]
&=&\frac {1}{s^{2}+10s+125} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)図1のフィードバック制御系全体の安定限界における三つの閉ループ極
(3)より,図1のフィードバック制御系全体の伝達関数\( \ G(s) \ \)は,
\[
\begin{eqnarray}
G(s) &=&\frac {\displaystyle \frac {K}{s}G_{\mathrm {f}}(s)}{\displaystyle 1+\frac {K}{s}G_{\mathrm {f}}(s)} \\[ 5pt ]
&=&\frac {\displaystyle \frac {K}{s}\frac {1}{s^{2}+10s+125}}{\displaystyle 1+\frac {K}{s}\frac {1}{s^{2}+10s+125}} \\[ 5pt ]
&=&\frac {K}{s^{3}+10s^{2}+125s+K} \\[ 5pt ]
\end{eqnarray}
\]
となり,特性方程式は,\( \ s^{3}+10s^{2}+125s+K=0 \ \)となる。ラウスの安定判別を用いてラウスの表を作成すると,
\[
\begin{array}{c|ccc}
& 1列 & 2列 \\
\hline
1行 & 1 & 125 \\
2行 & 10 & K \\
3行 & \frac {1250-K}{10} & 0 \\
4行 & K & 0 \\
\end{array}
\]
となるので,安定限界は,
\[
\begin{eqnarray}
\frac {1250-K}{10} &=&0 \\[ 5pt ]
K&=&1250 \\[ 5pt ]
\end{eqnarray}
\]
となる。よって特性方程式は\( \ s^{3}+10s^{2}+125s+1250=0 \ \)となり,これを因数分解して三つの極を求めると,
\[
\begin{eqnarray}
s^{3}+10s^{2}+125s+1250 &=&0 \\[ 5pt ]
s\left( s^{2}+125\right) +10\left( s^{2}+125\right) &=&0 \\[ 5pt ]
\left( s+10\right) \left( s^{2}+125\right) &=&0 \\[ 5pt ]
s&=&-10,±\mathrm {j}5\sqrt {5} \\[ 5pt ]
\end{eqnarray}
\]
となる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん