《機械・制御》〈回転機〉[R03:問3]三相誘導電動機の無負荷試験、拘束試験に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

三相誘導電動機に関して，次の問に答えよ。

(1)　次に示す記号を用いて，三相誘導機の星形結線一相分の\( \ \mathrm {L} \ \)型等価回路を描け。

［等価回路に使用する記号］
\( \ V_{1} \ \)：一次相電圧，\( \ I_{1} \ \)：一次電流，\( \ I_{2}^{\prime } \ \)：二次電流の一次換算値，\( \ I_{0} \ \)：励磁電流，
\( \ r_{1} \ \)：一次巻線抵抗，\( \ r_{2}^{\prime } \ \)：二次巻線抵抗の一次換算値，
\( \ x \ \)：漏れリアクタンス（\( \ x=x_{1}+x_{2}^{\prime } \ \)とする。ただし，\( \ x_{1} \ \)：一次漏れリアクタンス，\( \ x_{2}^{\prime } \ \)：二次漏れリアクタンスの一次換算値），
\( \ s \ \)：滑り，\( \ g_{0} \ \)：励磁コンダクタンス，\( \ b_{0} \ \)：励磁サセプタンス

(2)　ある三相誘導電動機を試験したところ，次のような結果となった。

（Ⅰ）抵抗測定試験により室温\( \ t \ \mathrm {[℃]} \ \)において端子間の抵抗値は\( \ R_{1} \ \mathrm {[\Omega ]} \ \)であった。

（Ⅱ）無負荷試験において定格電圧\( \ V_{\mathrm {N}} \ \mathrm {[V]} \ \)，定格周波数を加えたところ，入力電流は\( \ I_{\mathrm {N}} \ \mathrm {[A]} \ \)，入力電力は\( \ P_{\mathrm {N}} \ \mathrm {[W]} \ \)であった。また，定格電圧から端子電圧を下げ安定運転できる最低値まで徐々に低下させ，端子電圧に対する入力電力を測定した。その結果をもとに，外挿して求めた電圧ゼロの点の電力は\( \ P_{\mathrm {m}} \ \mathrm {[W]} \ \)であった。

（Ⅲ）拘束試験において定格周波数の三相交流電圧\( \ V_{\mathrm {s}} \ \mathrm {[V]} \ \)を加えたところ，入力電流は\( \ I_{\mathrm {s}} \ \mathrm {[A]} \ \)，入力電力は\( \ P_{\mathrm {s}} \ \mathrm {[W]} \ \)であった。

以上の試験により得られた結果から，等価回路定数\( \ r_{1} \ \)，\( \ r_{2}^{\prime } \ \)，\( \ x \ \)，\( \ g_{0} \ \)，\( \ b_{0} \ \)を求める式を導出せよ。導出にあたっては，仮定，及び導出の考え方を示すこと。

なお，等価回路の基準温度は\( \ T \ \mathrm {[℃]} \ \)とし，ある温度\( \ t \ \mathrm {[℃]} \ \)における抵抗値\( \ R\left( t\right) \ \)は次の式に従うとする。
\[
\begin{eqnarray}
R\left( t\right) &=&R\left( 0\right) \left[ 1+\alpha _{0} \left( t-0\right) \right] \\[ 5pt ] \end{eqnarray}
\] ここで，\( \ R\left( 0\right) \ \)は\( \ 0 \ \mathrm {℃} \ \)における抵抗値であり，\( \ \alpha _{0} \ \)は\( \ 0 \ \mathrm {℃} \ \)における銅の温度係数である。なお，\( \ \displaystyle \alpha _{0}=\frac {1}{235} \ \left[ \left( ℃\right) ^{-1} \right] \ \)とする。

【ワンポイント解説】

誘導電動機の各パラメータを求める問題です。
(1)は非常に易しい問題ですが，(2)は機械損の考え方が含まれる\( \ 1 \ \)種らしい問題であったかと思います。内容はそれほど難しくはありませんが，所々引っ掛けとなっている箇所があるので，気を付けるようにしましょう。

1.誘導電動機の\( \ \mathrm {L} \ \)形等価回路
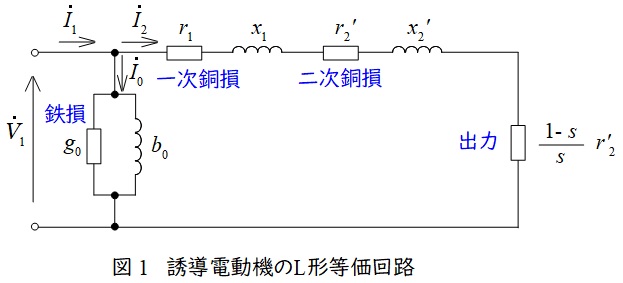
誘導電動機の\( \ \mathrm {L} \ \)形等価回路は図1のようになります。図1において，\( \ {\dot V}_{1} \ \)は一次側端子電圧，\( \ {\dot I}_{1} \ \)は一次電流，\( \ {\dot I}_{2} \ \)は二次電流，\( \ {\dot I}_{0} \ \)は励磁電流，\( \ r_{1} \ \)は一次巻線抵抗，\( \ r_{2}^{\prime } \ \)は二次巻線抵抗の一次換算，\( \ x_{1} \ \)は一次漏れリアクタンス，\( \ x_{2}^{\prime } \ \)は二次漏れリアクタンスの一次換算，\( \ s \ \)は滑りとなります。
\( \ \mathrm {L} \ \)形等価回路は一相分の等価回路の励磁回路を左端に寄せた簡易等価回路ですが，電験では圧倒的に多く使用する等価回路となります。

2.誘導電動機の無負荷試験
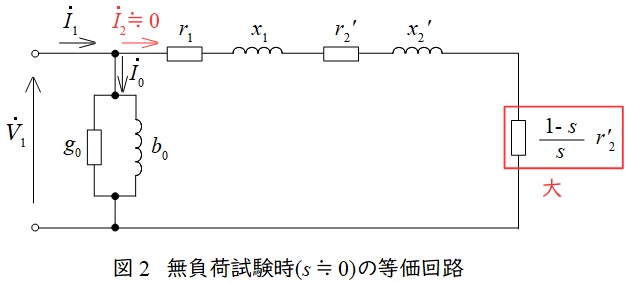
無負荷試験は，文字通り無負荷で運転したときの試験で，図2に示すように無負荷の時は電動機はほぼ同期速度で回転するため，滑り\( \ s≒0 \ \)となります。したがって，電源から出た電流はほぼ励磁回路に流れるので，一次側に定格電圧\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \)をかけ，そのときの電力\( \ P_{\mathrm {0}} \ \mathrm {[W]} \ \)と電流\( \ I_{\mathrm {0}} \ \mathrm {[A]} \ \)を測定すれば，励磁コンダクタンス\( \ g_{0} \ \mathrm {[S]} \ \)と励磁サセプタンス\( \ b_{0} \ \mathrm {[S]} \ \)をそれぞれ，
\[
\begin{eqnarray}
P_{\mathrm {0}} &=&3g_{0}\left( \frac {V_{\mathrm {n}}}{\sqrt {3}}\right) ^{2} \\[ 5pt ] &=&g_{0}V_{\mathrm {n}} ^{2} \\[ 5pt ] g_{0}&=&\frac {P_{\mathrm {0}}}{V_{\mathrm {n}}^{2}} \\[ 5pt ] b_{0}&=&\sqrt {Y_{\mathrm {0}}^{2}-g_{\mathrm {0}}^{2}} \\[ 5pt ] &=&\sqrt {\left( \frac {\sqrt {3}I_{\mathrm {0}}}{V_{\mathrm {n}}}\right) ^{2}-g_{\mathrm {0}}^{2}} \\[ 5pt ] \end{eqnarray}
\] と求めることができます。

3.誘導電動機の拘束試験
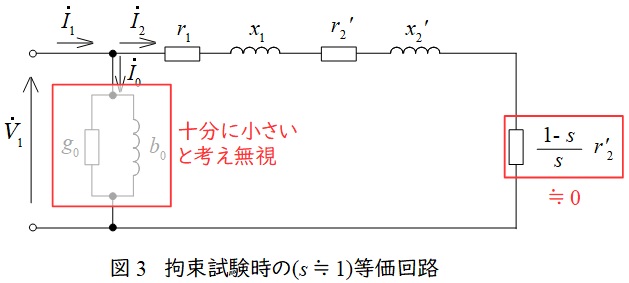
拘束試験は誘導電動機の回転子を拘束した時の試験で，回転子を回転しない場合滑り\( \ s≒1 \ \)と考えることができます。また，拘束試験において定格電流を流してもさほど大きな電圧はかからないので，励磁電流は十分に小さいと仮定すれば等価回路は図3のようになります。
このとき，一次側に定格電流\( \ I_{\mathrm {1n}} \ \mathrm {[A]} \ \)が流れるように電圧\( \ V_{\mathrm {s}} \ \mathrm {[V]} \ \)をかけ，そのときの電力\( \ P_{\mathrm {s}} \ \mathrm {[W]} \ \)を測定すれば，一次巻線抵抗と二次巻線抵抗の一次換算値の合計\( \ r=r_{1}+r_{2}^{\prime } \ \)と，一次漏れリアクタンスと二次漏れリアクタンスの一次換算値の合計\( \ x=x_{1}+x_{2}^{\prime } \ \)が，
\[
\begin{eqnarray}
P_{\mathrm {s}} &=&3rI_{\mathrm {1n}}^{2} \\[ 5pt ] r&=&\frac {P_{\mathrm {s}}}{3I_{\mathrm {1n}}^{2}} \\[ 5pt ] x&=&\sqrt {Z_{\mathrm {s}}^{2}-r^{2}} \\[ 5pt ] &=&\sqrt {\left( \frac {V_{\mathrm {s}}}{\sqrt {3}I_{\mathrm {1n}}}\right) ^{2}-r^{2}} \\[ 5pt ] \end{eqnarray}
\] と求めることができます。

【解答】

(1)三相誘導機の星形結線一相分の\( \ \mathrm {L} \ \)型等価回路を描く
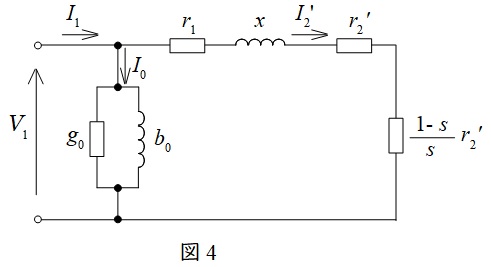
ワンポイント解説「1.誘導電動機の\( \ \mathrm {L} \ \)形等価回路」の通り，題意に沿って等価回路を描くと図4のようになる。

(2)試験により得られた結果から，等価回路定数\( \ r_{1} \ \)，\( \ r_{2}^{\prime } \ \)，\( \ x \ \)，\( \ g_{0} \ \)，\( \ b_{0} \ \)を求める式を導出
（Ⅰ）抵抗測定試験より，\( \ t \ \mathrm {[℃]} \ \)における抵抗値\( \ R\left( t\right) \ \)及び\( \ T \ \mathrm {[℃]} \ \)における抵抗値\( \ R\left( T\right) \ \)は，
\[
\begin{eqnarray}
R\left( t\right) &=&R\left( 0\right) \left[ 1+\alpha _{0} \left( t-0\right) \right]　&& \\[ 5pt ] &=&R\left( 0\right) \left( 1+\alpha _{0} t \right)　&・・・・・・・・・　①& \\[ 5pt ] R\left( T\right) &=&R\left( 0\right) \left[ 1+\alpha _{0} \left( T-0\right) \right]　&& \\[ 5pt ] &=&R\left( 0\right) \left( 1+\alpha _{0} T \right)　&・・・・・・・・・　②& \\[ 5pt ] \end{eqnarray}
\] となるので，\( \ ②÷① \ \)より，
\[
\begin{eqnarray}
\frac {R\left( T\right)}{R\left( t\right) } &=&\frac { 1+\alpha _{0}T }{1+\alpha _{0} t } \\[ 5pt ] R\left( T\right) &=&\frac { 1+\alpha _{0}T }{1+\alpha _{0} t }R\left( t\right) \\[ 5pt ] \end{eqnarray}
\] となる。\( \ t \ \mathrm {[℃]} \ \)での任意の\( \ 2 \ \)相の端子間の抵抗値が\( \ R_{1} \ \mathrm {[\Omega ]} \ \)なので，\( \ 1 \ \)相あたりの抵抗値\( \ \displaystyle R\left( t\right) =\frac {R_{1}}{2} \ \mathrm {[\Omega ]} \ \)であるから，
\[
\begin{eqnarray}
r_{1} &=&\frac { 1+\alpha _{0}T }{1+\alpha _{0} t }\cdot \frac {R_{1}}{2} \\[ 5pt ] &=&\frac { \displaystyle 1+\frac {1}{235}T }{\displaystyle 1+\frac {1}{235} t }\cdot \frac {R_{1}}{2} \\[ 5pt ] &=&\frac { 235+T }{235+t }\cdot \frac {R_{1}}{2} \\[ 5pt ] \end{eqnarray}
\] と求められる。

（Ⅱ）無負荷試験より，励磁回路での消費電力\( \ P_{\mathrm {0}}=P_{\mathrm {N}}-P_{\mathrm {m}} \ \)であるから，励磁コンダクタンス\( \ g_{0} \ \)及び励磁サセプタンス\( \ b_{0} \ \)は，ワンポイント解説「2.誘導電動機の無負荷試験」の通り，
\[
\begin{eqnarray}
P_{\mathrm {0}} &=&3g_{0}\left( \frac {V_{\mathrm {N}}}{\sqrt {3}}\right) ^{2} \\[ 5pt ] &=&g_{0}V_{\mathrm {N}} ^{2} \\[ 5pt ] g_{0}&=&\frac {P_{\mathrm {0}}}{V_{\mathrm {N}}^{2}} \\[ 5pt ] &=&\frac {P_{\mathrm {N}}-P_{\mathrm {m}}}{V_{\mathrm {N}}^{2}} \\[ 5pt ] b_{0}&=&\sqrt {Y_{\mathrm {0}}^{2}-g_{\mathrm {0}}^{2}} \\[ 5pt ] &=&\sqrt {\left( \frac {\sqrt {3}I_{\mathrm {N}}}{V_{\mathrm {N}}}\right) ^{2}-\left( \frac {P_{\mathrm {N}}-P_{\mathrm {m}}}{V_{\mathrm {N}}^{2}}\right) ^{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

（Ⅲ）拘束試験において，励磁回路に流れる電流は十分に小さく，また拘束しているので外挿して求めた電圧ゼロの点の電力すなわち機械損\( \ P_{\mathrm {m}} \ \mathrm {[W]} \ \)は零と考えられる。したがって，二次巻線抵抗の一次換算値\( \ r_{2}^{\prime } \ \)及び一次漏れリアクタンスと二次漏れリアクタンスの一次換算値の合計値\( \ x=x_{1}+x_{2}^{\prime } \ \)は，ワンポイント解説「3.誘導電動機の拘束試験」の通り，
\[
\begin{eqnarray}
P_{\mathrm {s}} &=&3\left( r_{1}+r_{2}^{\prime }\right) I_{\mathrm {s}}^{2} \\[ 5pt ] r_{1}+r_{2}^{\prime }&=&\frac {P_{\mathrm {s}}}{3I_{\mathrm {s}}^{2}} \\[ 5pt ] r_{2}^{\prime }&=&\frac {P_{\mathrm {s}}}{3I_{\mathrm {s}}^{2}}-r_{1} \\[ 5pt ] &=&\frac {P_{\mathrm {s}}}{3I_{\mathrm {s}}^{2}}-\frac { 235+T }{235+t }\cdot \frac {R_{1}}{2} \\[ 5pt ] x&=&\sqrt {Z_{\mathrm {s}}^{2}-\left( r_{1}+r_{2}^{\prime }\right) ^{2}} \\[ 5pt ] &=&\sqrt {\left( \frac {V_{\mathrm {s}}}{\sqrt {3}I_{\mathrm {s}}}\right) ^{2}-\left( \frac {P_{\mathrm {s}}}{3I_{\mathrm {s}}^{2}}\right) ^{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。