【問題】
【難易度】★★★☆☆(普通)
三相星形接続の同期発電機が三相平衡負荷に接続されており,発電機の各定数が以下の記号で示される。
\( \ X_{\mathrm {d}} \ \mathrm {[\Omega ]} \ \):直軸(\( \ \mathrm {d} \ \)軸)同期リアクタンス,\( \ X_{\mathrm {q}} \ \mathrm {[\Omega ]} \ \):横軸(\( \ \mathrm {q} \ \)軸)同期リアクタンス,\( \ E \ \mathrm {[V]} \ \):無負荷誘導起電力(相電圧),\( \ V \ \mathrm {[V]} \ \):端子電圧(相電圧),\( \ I_{\mathrm {a}} \ \mathrm {[A]} \ \):電機子電流,\( \ I_{\mathrm {d}} \ \mathrm {[A]} \ \):電機子電流の直軸(\( \ \mathrm {d} \ \)軸)成分,\( \ I_{\mathrm {q}} \ \mathrm {[A]} \ \):電機子電流の横軸(\( \ \mathrm {q} \ \)軸)成分,\( \ \phi \ \mathrm {[rad]} \ \):力率角(遅れ),\( \ \delta \ \mathrm {[rad]} \ \):負荷角(内部相差角)
この同期発電機の電機子巻線抵抗が無視できるとし,以下の問に答えよ。
(1) この三相同期発電機が遅れ力率で運転しているときのフェーザ図を示し,図中に\( \ \dot E \ \),\( \ \dot V \ \),\( \ {\dot I}_{\mathrm {a}} \ \),\( \ \mathrm {j}X_{\mathrm {d}}{\dot I}_{\mathrm {d}} \ \),\( \ \mathrm {j}X_{\mathrm {q}}{\dot I}_{\mathrm {q}} \ \),\( \ \phi \ \),\( \ \delta \ \)を記入せよ。ただし,\( \ \mathrm {q} \ \)軸は\( \ \dot E \ \)の正方向とし,\( \ \mathrm {q} \ \)軸の\( \ \displaystyle \frac {\pi }{2} \ \)遅れに\( \ \mathrm {d} \ \)軸をとること。
(2) 発電機の出力\( \ P \ \mathrm {[W]} \ \)を\( \ E \ \),\( \ V \ \),\( \ X_{\mathrm {d}} \ \),\( \ X_{\mathrm {q}} \ \),\( \ \delta \ \)を用いて表せ。
(3) \( \ X_{\mathrm {d}}=0.9 \ \mathrm {\Omega } \ \),\( \ X_{\mathrm {q}}=0.7 \ \mathrm {\Omega } \ \),\( \ I_{\mathrm {a}}=200 \ \mathrm {[A]} \ \),\( \ V=400 \ \mathrm {V} \ \),\( \ \displaystyle \phi +\delta =\frac {\pi }{6} \ \)であるとき,三相同期発電機の無負荷誘導起電力(相電圧)\( \ E_{1} \ \mathrm {[V]} \ \)を求めよ。
(4) \( \ X_{\mathrm {d}} \ \),\( \ X_{\mathrm {q}} \ \),\( \ I_{\mathrm {a}} \ \),\( \ V \ \)が小問(3)の値と等しいとき,力率\( \ =1 \ \)とする際の\( \ \sin \delta \ \)の値を求めよ。
(5) \( \ X_{\mathrm {d}} \ \),\( \ X_{\mathrm {q}} \ \),\( \ I_{\mathrm {a}} \ \),\( \ V \ \)が小問(3)の値と等しいとき,力率\( \ =1 \ \)とする際の無負荷誘導起電力(相電圧)\( \ E_{2} \ \mathrm {[V]} \ \)を求めよ。
【ワンポイント解説】
同期発電機の特性に関する問題です。
特に問題文では触れられていませんが,直軸(\( \ \mathrm {d} \ \)軸)同期リアクタンスと横軸(\( \ \mathrm {q} \ \)軸)同期リアクタンスの記載があるので,突極形同期発電機と判断します。(\( \ 1 \ \)種では突極形同期発電機のベクトル図は必須の知識です。)
(3)以降が易しめなので,(1)が分かっていれば高得点を狙える問題であると思います。
1.突極形同期発電機の構造及びベクトル図
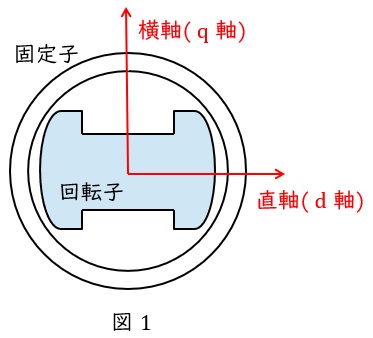
突極形同期発電機の構造は図1のようになり,回転子の磁極と同じ向きの軸を直軸(\( \ \mathrm {d} \ \)軸),磁極と直角の向きの軸を横軸(\( \ \mathrm {q} \ \)軸)といいます。
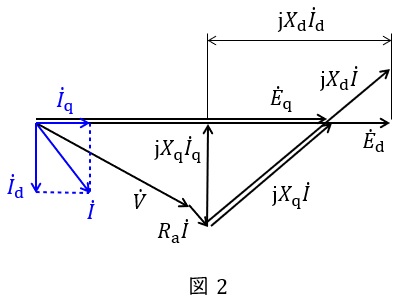
円筒機は直軸同期リアクタンス\( \ X_{\mathrm {d}} \ \)と横軸同期リアクタンス\( \ X_{\mathrm {q}} \ \)がほぼ等しいので,基本的な同期発電機の等価回路やベクトル図が適用できますが,突極機の場合はその構造上\( \ X_{\mathrm {d}}>X_{\mathrm {q}} \ \)となるので,ベクトル図としては図2のようになります。
図2において,\( \ {\dot E}_{\mathrm {d}} \ \):無負荷誘導起電力,\( \ {\dot E}_{\mathrm {q}} \ \):内部横軸リアクタンス電圧,\( \ \dot I \ \):電機子電流,\( \ {\dot I}_{\mathrm {d}} \ \):電機子電流の直軸分,\( \ {\dot I}_{\mathrm {q}} \ \):電機子電流の横軸分,\( \ R_{\mathrm {a}} \ \):電機子抵抗(無視することも多い),となります。
2.突極形同期発電機の直軸同期リアクタンスと横軸同期リアクタンスの違い
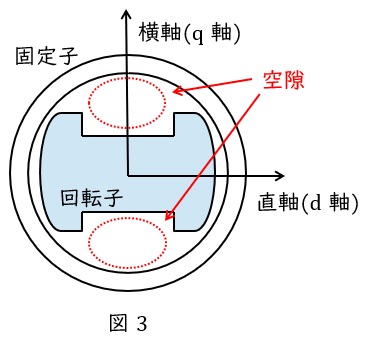
円筒形同期発電機は直軸方向と横軸方向の透磁率の違いはほとんどありませんが,突極形同期発電機は図3に示すように,横軸方向に空隙がある分横軸方向の方が透磁率は小さくなります。
透磁率が小さいと磁気抵抗\( \ \displaystyle R_{\mathrm {m}}\left( =\frac {l}{\mu S}\right) \ \)が大きくなります。
磁気抵抗\( \ \displaystyle R_{\mathrm {m}} \ \)が大きいと,インダクタンス\( \ \displaystyle L\left( =\frac {N^{2}}{R_{\mathrm {m}}}\right) \ \)は小さくなります。
よって,突極形同期発電機においては直軸同期リアクタンス\( \ X_{\mathrm {d}} \ \)の方が横軸同期リアクタンス \( \ X_{\mathrm {q}} \ \)より大きくなります。
【解答】
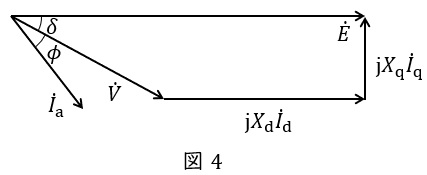
(1)三相同期発電機が遅れ力率で運転しているときのフェーザ図
ワンポイント解説「1.突極形同期発電機の構造及びベクトル図」の通り,\( \ \dot E \ \),\( \ \dot V \ \),\( \ {\dot I}_{\mathrm {a}} \ \),\( \ \mathrm {j}X_{\mathrm {d}}{\dot I}_{\mathrm {d}} \ \),\( \ \mathrm {j}X_{\mathrm {q}}{\dot I}_{\mathrm {q}} \ \),\( \ \phi \ \),\( \ \delta \ \)を用いてフェーザ図を描くと図4のようになる。
(2)発電機の出力\( \ P \ \mathrm {[W]} \ \)を\( \ E \ \),\( \ V \ \),\( \ X_{\mathrm {d}} \ \),\( \ X_{\mathrm {q}} \ \),\( \ \delta \ \)を用いて表す
端子電圧\( \ V \ \)と電機子電流\( \ I_{\mathrm {a}} \ \)を直軸成分\( \ I_{\mathrm {d}} \ \)と横軸成分\( \ I_{\mathrm {q}} \ \)に分解したフェーザ図は図5のようになる。
これより,発電機の出力\( \ P \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P &=&3\left( V\cos \delta I_{\mathrm {q}}+V\sin \delta I_{\mathrm {d}}\right) \\[ 5pt ]
\end{eqnarray}
\]
であり,図5より,
\[
\begin{eqnarray}
E-X_{\mathrm {d}}I_{\mathrm {d}} &=&V\cos \delta \\[ 5pt ]
X_{\mathrm {d}}I_{\mathrm {d}} &=&E-V\cos \delta \\[ 5pt ]
I_{\mathrm {d}} &=&\frac {E-V\cos \delta }{X_{\mathrm {d}}} \\[ 5pt ]
\end{eqnarray}
\]
及び
\[
\begin{eqnarray}
X_{\mathrm {q}}I_{\mathrm {q}} &=&V\sin \delta \\[ 5pt ]
I_{\mathrm {q}} &=&\frac {V\sin \delta }{X_{\mathrm {q}}} \\[ 5pt ]
\end{eqnarray}
\]
であることから,\( \ P \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P &=&3\left( V\cos \delta I_{\mathrm {q}}+V\sin \delta I_{\mathrm {d}}\right) \\[ 5pt ]
&=&3\left( V\cos \delta \cdot \frac {V\sin \delta }{X_{\mathrm {q}}}+V\sin \delta \cdot \frac {E-V\cos \delta }{X_{\mathrm {d}}}\right) \\[ 5pt ]
&=&3\left( \frac {V^{2}\sin \delta \cos \delta }{X_{\mathrm {q}}}+\frac {VE}{X_{\mathrm {d}}}\sin \delta -\frac {V^{2}\sin \delta \cos \delta }{X_{\mathrm {d}}}\right) \\[ 5pt ]
&=&\frac {3VE}{X_{\mathrm {d}}}\sin \delta +3V^{2}\left( \frac {1}{X_{\mathrm {q}}}-\frac {1}{X_{\mathrm {d}}}\right) \sin \delta \cos \delta \\[ 5pt ]
&=&\frac {3VE}{X_{\mathrm {d}}}\sin \delta +\frac {3V^{2}}{2}\left( \frac {1}{X_{\mathrm {q}}}-\frac {1}{X_{\mathrm {d}}}\right) \sin 2\delta \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
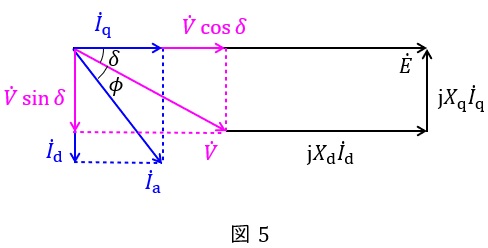
(3)三相同期発電機の無負荷誘導起電力(相電圧)\( \ E_{1} \ \mathrm {[V]} \ \)
図5より,
\[
\begin{eqnarray}
E_{\mathrm {1}} &=&V\cos \delta +X_{\mathrm {d}}I_{\mathrm {d}} \\[ 5pt ]
&=&\sqrt {V^{2}-\left( X_{\mathrm {q}}I_{\mathrm {q}}\right) ^{2}} +X_{\mathrm {d}}I_{\mathrm {a}}\sin \left( \phi +\delta \right) \\[ 5pt ]
&=&\sqrt {V^{2}-\left\{ X_{\mathrm {q}}I_{\mathrm {a}}\cos \left( \phi +\delta \right) \right\} ^{2}} +X_{\mathrm {d}}I_{\mathrm {a}}\sin \left( \phi +\delta \right) \\[ 5pt ]
\end{eqnarray}
\]
であるので,各値を代入すると,
\[
\begin{eqnarray}
E_{\mathrm {1}} &=&\sqrt {400^{2}-\left( 0.7\times 200\times \cos \frac {\pi}{6} \right) ^{2}} +0.9\times 200\times \sin \frac {\pi}{6} \\[ 5pt ]
&=&\sqrt {160 \ 000-\left( 140\times \frac {\sqrt{3}}{2} \right) ^{2}} +180\times \frac {1}{2} \\[ 5pt ]
&=&\sqrt {160 \ 000-14 \ 700} +90 \\[ 5pt ]
&≒&471.18 → 471 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)力率\( \ =1 \ \)とする際の\( \ \sin \delta \ \)の値
力率\( \ =1 \ \)のときのフェーザ図は図6のようになる。
図6より,
\[
\begin{eqnarray}
V\sin \delta &=&X_{\mathrm {q}}I_{\mathrm {q}} \\[ 5pt ]
&=&X_{\mathrm {q}}I_{\mathrm {a}}\cos \delta \\[ 5pt ]
&=&X_{\mathrm {q}}I_{\mathrm {a}}\sqrt {1-\sin ^{2}\delta } \\[ 5pt ]
V^{2}\sin ^{2}\delta &=&\left( X_{\mathrm {q}}I_{\mathrm {a}}\right) ^{2}\left( 1-\sin ^{2}\delta \right) \\[ 5pt ]
\left\{ V^{2}+\left( X_{\mathrm {q}}I_{\mathrm {a}}\right) ^{2}\right\} \sin ^{2}\delta &=&\left( X_{\mathrm {q}}I_{\mathrm {a}}\right) ^{2} \\[ 5pt ]
\sin ^{2}\delta &=&\frac {\left( X_{\mathrm {q}}I_{\mathrm {a}}\right) ^{2}}{V^{2}+\left( X_{\mathrm {q}}I_{\mathrm {a}}\right) ^{2}} \\[ 5pt ]
\sin \delta &=&\frac {X_{\mathrm {q}}I_{\mathrm {a}}}{\sqrt {V^{2}+\left( X_{\mathrm {q}}I_{\mathrm {a}}\right) ^{2}}} \\[ 5pt ]
&=&\frac {0.7\times 200}{\sqrt {400^{2}+\left( 0.7\times 200\right) ^{2}}} \\[ 5pt ]
&≒&0.330 \ 35 → 0.330 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
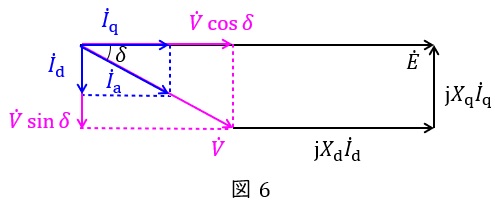
(5)力率\( \ =1 \ \)とする際の無負荷誘導起電力(相電圧)\( \ E_{2} \ \mathrm {[V]} \ \)
図6より,
\[
\begin{eqnarray}
E_{\mathrm {2}} &=&V\cos \delta +X_{\mathrm {d}}I_{\mathrm {d}} \\[ 5pt ]
&=&V\cos \delta +X_{\mathrm {d}}I_{\mathrm {a}}\sin \delta \\[ 5pt ]
\end{eqnarray}
\]
であり,
\[
\begin{eqnarray}
\cos \delta &=&\sqrt {1-\sin ^{2}\delta } \\[ 5pt ]
&=&\sqrt {1-0.330 \ 35^{2}} \\[ 5pt ]
&≒&0.943 \ 86 \\[ 5pt ]
\end{eqnarray}
\]
なので,各値を代入すれば,
\[
\begin{eqnarray}
E_{\mathrm {2}} &=&400\times 0.943 \ 86 +0.9\times 200\times 0.330 \ 35 \\[ 5pt ]
&≒&437.01 → 437 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。





















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん