【問題】
【難易度】★☆☆☆☆(易しい)
伝達関数\( \ G\left( s \right) \ \)が次式で表されるシステムについて,以下の問に答えよ。
\[
\begin{eqnarray}
G\left( s \right) &=& \frac {1 \ 000}{s^{2}+as+100} \\[ 5pt ]
\end{eqnarray}
\]
(1) \( \ a=20 \ \)としたとき,\( \ G\left( s \right) \ \)のベクトル軌跡は,位相が\( \ 90° \ \)遅れたとき虚軸と交わる。このときのゲイン\( \ \left| G\left( \mathrm {j}\omega \right) \right| \ \)を求めよ。
(2) \( \ a=20 \ \)としたとき,\( \ G\left( s \right) \ \) のボード線図の折れ線近似を考える。この折れ線近似において,角周波数が\( \ 100 \ \mathrm {rad / s} \ \)であるときのゲインを求めデシベルで表せ。
(3) \( \ a=10 \ \)としたとき,ゲイン\( \ \left| G\left( \mathrm {j}\omega \right) \right| \ \)を求めよ。
次に,小問(3)で求めたゲイン\( \ \left| G\left( \mathrm {j}\omega \right) \right| \ \)の最大値(共振値)\( \ M_{\mathrm {p}} \ \)とそのときの角周波数(共振角周波数)\( \ \omega _{\mathrm {p}} \ \)を求めよう。以下の問に答えよ。
(4) 変数変換\( \ x=\omega ^{2} \ \)を施すことで,小問(3)で求めたゲイン\( \ \left| G\left( \mathrm {j}\omega \right) \right| \ \)の式を\( \ \displaystyle \frac {1 \ 000}{\sqrt {f\left( x \right) }} \ \)の形に変形することを考える。\( \ f\left( x \right) \ \)の最小値とそのときの\( \ x \ \)を求めよ。
(5) \( \ M_{\mathrm {p}} \ \)と\( \ \omega _{\mathrm {p}} \ \)を求めよ。
【ワンポイント解説】
与えられている伝達関数から周波数伝達関数とゲインを導出する問題です。
(1)の考え方に迷う部分はあるかもしれませんが,\( \ 1 \ \)種の自動制御の問題としてはかなり易しい問題になるかと思います。
計算間違いに注意して確実に高得点できるようにしましょう。
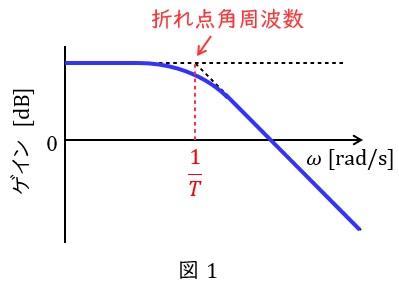
1.ボード線図
周波数伝達関数が\( \ \displaystyle W(\mathrm {j}\omega ) =\frac {K}{1+\mathrm {j}\omega T} \ \)で与えられる時,ゲイン\( \ g \ \mathrm {[dB]} \ \)は,
\[
\begin{eqnarray}
g&=&20\log _{10} \left| W(\mathrm {j}\omega )\right| \\[ 5pt ]
&=&20\log _{10} \frac {K}{\sqrt {1+\left( \omega T\right) ^{2}}} \ \mathrm {[dB]} \\[ 5pt ]
\end{eqnarray}
\]
となりますが,\( \ \displaystyle \omega \ll \frac {1}{T} \ \)すなわち\( \ \omega T \ll 1 \ \)のとき,
\[
\begin{eqnarray}
g&≃&20\log _{10} \frac {K}{\sqrt {1+0}} \\[ 5pt ]
&=&20\log _{10}K \\[ 5pt ]
\end{eqnarray}
\]
とほぼ一定の値となり,\( \ \displaystyle \omega \gg \frac {1}{T} \ \)すなわち\( \ \omega T \gg 1 \ \)のとき,
\[
\begin{eqnarray}
g&≃&20\log _{10} \frac {K}{\sqrt {\left( \omega T\right) ^{2}}} \\[ 5pt ]
&=&20\log _{10} \frac {K}{\omega T} \\[ 5pt ]
&=&20\log _{10} K-20\log _{10}\omega T \\[ 5pt ]
\end{eqnarray}
\]
となり,横軸に対数座標をとると,ほぼ直線的に減少していくことになります。したがって,ボード線図は図1のようになります。
図1において\( \ \displaystyle \omega =\frac {1}{T} \ \)となる角周波数を折れ点角周波数と呼びます。
【解答】
(1)\( \ a=20 \ \)としたときのゲイン\( \ \left| G\left( \mathrm {j}\omega \right) \right| \ \)
\( \ a=20 \ \)としたとき,伝達関数\( \ G\left( s \right) \ \)は,
\[
\begin{eqnarray}
G\left( s \right) &=& \frac {1 \ 000}{s^{2}+20s+100} \\[ 5pt ]
\end{eqnarray}
\]
であり,周波数伝達関数\( \ G\left( \mathrm {j}\omega \right) \ \)は,
\[
\begin{eqnarray}
G\left( \mathrm {j}\omega \right) &=& \frac {1 \ 000}{-\omega ^{2}+\mathrm {j}20\omega +100} \\[ 5pt ]
&=& \frac {1 \ 000}{100-\omega ^{2}+\mathrm {j}20\omega } \\[ 5pt ]
\end{eqnarray}
\]
なので,ゲイン\( \ \left| G\left( \mathrm {j}\omega \right) \right| \ \)は,
\[
\begin{eqnarray}
\left| G\left( \mathrm {j}\omega \right) \right| &=& \frac {1 \ 000}{\sqrt {\left( 100-\omega ^{2}\right) ^{2}+\left( 20\omega \right) ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,ベクトル軌跡が虚軸と交わるのは周波数伝達関数の実部が零のときであるから,
\[
\begin{eqnarray}
100-\omega ^{2} &=& 0 \\[ 5pt ]
\omega ^{2} &=& 100 \\[ 5pt ]
\omega &=& 10 \ \mathrm {[rad / s]} \\[ 5pt ]
\end{eqnarray}
\]
の時であり,このときの\( \ \left| G\left( \mathrm {j}\omega \right) \right| \ \)は,
\[
\begin{eqnarray}
\left| G\left( \mathrm {j}10 \right) \right| &=& \frac {1 \ 000}{\sqrt {\left( 100-10^{2}\right) ^{2}+\left( 20\times 10 \right) ^{2}}} \\[ 5pt ]
&=& 5 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)折れ線近似において,角周波数が\( \ 100 \ \mathrm {rad / s} \ \)であるときのゲイン
ゲイン\( \ \left| G\left( \mathrm {j}\omega \right) \right| \ \)の式を変形すると,
\[
\begin{eqnarray}
\left| G\left( \mathrm {j}\omega \right) \right| &=& \frac {1 \ 000}{\sqrt {\left( 100-\omega ^{2}\right) ^{2}+\left( 20\omega \right) ^{2}}} \\[ 5pt ]
&=& \frac {1 \ 000}{\sqrt {10 \ 000+200\omega ^{2}+\omega ^{4}}} \\[ 5pt ]
&=& \frac {1 \ 000}{\sqrt {\left( 100+\omega ^{2}\right) ^{2}}} \\[ 5pt ]
&=& \frac {1 \ 000}{100+\omega ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「1.ボード線図」の通り,\( \ \omega =100 \ \mathrm {[rad / s]} \ \)のとき,\( \ 100≪\omega ^{2} \ \)と考えればよいから,デシベルで表したときのゲイン\( \ g=20\log _{10} \left| G(\mathrm {j}\omega )\right| \ \mathrm {[dB]} \ \)は,
\[
\begin{eqnarray}
g &≃& 20\log _{10} \frac {1 \ 000}{\omega ^{2}} \\[ 5pt ]
&=& 20\log _{10} \frac {1 \ 000}{100 ^{2}} \\[ 5pt ]
&=& 20\log _{10} \frac {1}{10} \\[ 5pt ]
&=& -20\log _{10} 10 \\[ 5pt ]
&=& -20 \ \mathrm {[dB]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ a=10 \ \)としたときのゲイン\( \ \left| G\left( \mathrm {j}\omega \right) \right| \ \)
\( \ a=10 \ \)としたとき,伝達関数\( \ G\left( s \right) \ \)は,
\[
\begin{eqnarray}
G\left( s \right) &=& \frac {1 \ 000}{s^{2}+10s+100} \\[ 5pt ]
\end{eqnarray}
\]
であり,周波数伝達関数\( \ G\left( \mathrm {j}\omega \right) \ \)は,
\[
\begin{eqnarray}
G\left( \mathrm {j}\omega \right) &=& \frac {1 \ 000}{-\omega ^{2}+\mathrm {j}10\omega +100} \\[ 5pt ]
&=& \frac {1 \ 000}{100-\omega ^{2}+\mathrm {j}10\omega } \\[ 5pt ]
\end{eqnarray}
\]
なので,ゲイン\( \ \left| G\left( \mathrm {j}\omega \right) \right| \ \)は,
\[
\begin{eqnarray}
\left| G\left( \mathrm {j}\omega \right) \right| &=& \frac {1 \ 000}{\sqrt {\left( 100-\omega ^{2}\right) ^{2}+\left( 10\omega \right) ^{2}}} \\[ 5pt ]
&=& \frac {1 \ 000}{\sqrt {10 \ 000-100\omega ^{2}+\omega ^{4}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)\( \ f\left( x \right) \ \)の最小値とそのときの\( \ x \ \)
(3)解答式において,\( \ x=\omega ^{2} \ \)とすれば\( \ f\left( x \right) \ \)は,
\[
\begin{eqnarray}
f\left( x \right) &=& 10 \ 000-100x+x ^{2} \\[ 5pt ]
\end{eqnarray}
\]
であり,微分して零となる\( \ x \ \)が最小となるので,
\[
\begin{eqnarray}
\frac {\mathrm {d}f\left( x \right) }{\mathrm {d}x}= -100+2x&=&0 \\[ 5pt ]
x&=&50 \\[ 5pt ]
\end{eqnarray}
\]
と求められ,このときの\( \ f\left( x \right) \ \)は,
\[
\begin{eqnarray}
f\left( 50 \right) &=& 10 \ 000-100\times 50+50 ^{2} \\[ 5pt ]
&=& 7 \ 500 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)\( \ M_{\mathrm {p}} \ \)と\( \ \omega _{\mathrm {p}} \ \)
\( \ x=50 \ \)のとき\( \ f\left( x \right) \ \)が最小値\( \ 7 \ 500 \ \)となるので,\( \ M_{\mathrm {p}} \ \)及び\( \ \omega _{\mathrm {p}} \ \)は,
\[
\begin{eqnarray}
M_{\mathrm {p}} &=& \frac {1 \ 000}{\sqrt {f\left( x \right) }} \\[ 5pt ]
&=& \frac {1 \ 000}{\sqrt {7 \ 500}} \\[ 5pt ]
&≒& 11.5 \\[ 5pt ]
\omega _{\mathrm {p}}&=& \sqrt {50} \\[ 5pt ]
&≒& 7.07 \ \mathrm {[rad / s]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん