《機械》〈電熱〉[H22:問4]電気加熱の中の電磁波による誘電加熱に関する空欄穴埋問題

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，電気加熱の中の電磁波による誘電加熱に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切な語句を解答群の中から選びなさい。

電磁波による誘電加熱の原理は次のとおりである。被加熱物である誘電体に電磁波の高周波電界が加えられると誘電体内の分子は\( \ \fbox {　 （１） 　} \ \)を生じる。この状態を生じる\( \ \fbox {　 （２） 　} \ \)の移動が電界の時間的変化に追随できなくなると，変位電流が電界に対して遅れを生じて電力損失が発生する。この現象が\( \ \fbox {　 （３） 　} \ \)による熱の発生であり，電磁波の誘電体内への浸透深さは\( \ \fbox {　 （４） 　} \ \)に反比例する。

電磁波による誘電加熱は，周波数帯によって次の\( \ 2 \ \)種類に大別される。その一つは\( \ 1 \ ～ \ 100 \ \mathrm {[MHz]} \ \)程度の周波数帯を使用する高周波加熱であり，他の一つは\( \ 300 \ \mathrm {[MHz]} \ ～ \ 30 \ \mathrm {[GHz]} \ \)程度の周波数帯を使用する\( \ \fbox {　 （５） 　} \ \)である。

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　マイクロ波加熱　　　　　　　&（ロ）&　荷電体　　　　　&（ハ）&　誘電損 \\[ 5pt ] &（ニ）&　電磁誘導　　　　　&（ホ）&　熱　損　　　　　&（ヘ）&　プラズマ加熱 \\[ 5pt ] &（ト）&　放射体　　　　　&（チ）&　磁性体　　　　　&（リ）&　電　離 \\[ 5pt ] &（ヌ）&　伝送損　　　　　&（ル）&　遠赤外加熱　　　　　　　&（ヲ）&　分　極 \\[ 5pt ] &（ワ）&　波形率　　　　　&（カ）&　周波数　　　　　&（ヨ）&　波　長 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

誘電加熱に関する問題です。
名称が似ている加熱方式に誘導加熱があり，こちらは令和2年問7に出題されています。
どちらも，電熱の範囲では出題されやすい印象がありますので，それぞれの違いを含めよく理解しておくようにして下さい。

1.誘電加熱
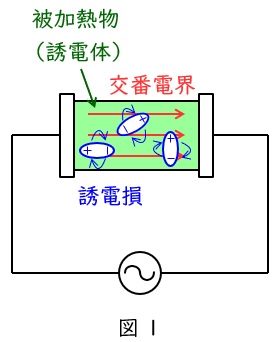
交番電界中に誘電体を置くことによって，誘電体に誘電損が生じ発熱することを利用した加熱方式です。
図1のように平行板電極に被加熱物（誘電体）を挿入し，高周波の電界を加えることで，誘電分極した電気双極子が振動・回転することにより発熱します。電子レンジはこの原理を利用した電化製品の一つです。

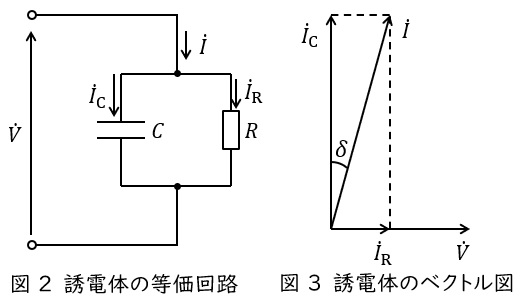
2.誘電正接\( \ \tan \delta \ \)
誘電体の等価回路は図2のように抵抗\( \ R \ \mathrm {[\Omega ]} \ \)と静電容量\( \ C \ \mathrm {[F]} \ \)の並列回路となり，コンデンサには図3のようなベクトル図の電流が流れます。この時の\( \ \displaystyle \frac {I_{\mathrm {R}}}{I_{\mathrm {C}}}=\tan \delta \ \)を誘電正接と呼びます。この等価回路における発熱にかかる誘電損\( \ W_{\mathrm {d}} \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
W_{\mathrm {d}}&=&VI_{\mathrm {R}} \\[ 5pt ] &=&VI_{\mathrm {C}}\tan \delta \\[ 5pt ] &=&V\omega CV\tan \delta \\[ 5pt ] &=&\omega CV^{2}\tan \delta \\[ 5pt ] &=&2\pi f \frac {\varepsilon _{\mathrm {r}}\varepsilon _{\mathrm {0}}S}{d}E^{2}d^{2}\tan \delta \\[ 5pt ] &=&2\pi fSdE^{2} \varepsilon _{\mathrm {0}}\varepsilon _{\mathrm {r}}\tan \delta \\[ 5pt ] \end{eqnarray}
\] となり，発熱量は，電界\( \ E \ \mathrm {[V / m]} \ \)の\( \ 2 \ \)乗に比例し，周波数\( \ f \ \mathrm {[Hz]} \ \)，比誘電率\( \ \varepsilon _{\mathrm {r}} \ \)，誘電正接\( \ \tan \delta \ \)に比例することがわかります。\( \ \varepsilon _{\mathrm {r}}\tan \delta \ \)を損失係数といいます。

3.電力半減深度\( \ D \ \)
誘電加熱において，電磁波の誘電体への浸透深さ\( \ D \ \mathrm {[m]} \ \)は，周波数\( \ f \ \mathrm {[Hz]} \ \)，比誘電率\( \ \varepsilon _{\mathrm {r}} \ \)，誘電正接\( \ \tan \delta \ \)とすると，
\[
\begin{eqnarray}
D&≒&\frac {3.32\times 10^{7}}{f\sqrt {\varepsilon _{\mathrm {r}}}\cdot \tan \delta } \\[ 5pt ] \end{eqnarray}
\] で求められます。一般のコンロでの加熱の強火と弱火の概念で考えればイメージしやすいかと思います。

【解答】

(1)解答：ヲ
題意より解答候補は，（ニ）電磁誘導，（リ）電離，（ヲ）分極，になると思います。
ワンポイント解説「1.誘電加熱」の通り，誘電体に電磁波の高周波電界が加えられると誘電体内の分子は分極を生じます。

(2)解答：ロ
題意より解答候補は，（ロ）荷電体，（ト）放射体，（チ）磁性体，になると思います。
電界の周波数が大きくなると荷電体の移動が電界の時間的変化に追随できなくなり，これにより電力損失が発生し発熱します。

(3)解答：ハ
題意より解答候補は，（ハ）誘電損，（ホ）熱損，（ヌ）伝送損，になると思います。
誘電加熱の熱の発生は誘電損による熱の発生となります。

(4)解答：カ
題意より解答候補は，（ワ）波形率，（カ）周波数，（ヨ）波長，になると思います。
ワンポイント解説「3.電力半減深度\( \ D \ \)」の通り，電磁波の誘電体内への浸透深さは周波数に反比例します。

(5)解答：イ
題意より解答候補は，（イ）マイクロ波加熱，（ヘ）プラズマ加熱，（ル）遠赤外加熱，になると思います。
\( \ 300 \ \mathrm {[MHz]} \ ～ \ 30 \ \mathrm {[GHz]} \ \)程度の周波数帯を使用する誘電加熱はマイクロ波加熱と呼ばれます。電子レンジがその代表例です。