《機械》〈パワーエレクトロニクス〉[R05:問4]交流から直流を得る整流回路に関する空欄穴埋問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，直流電源を得る回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。

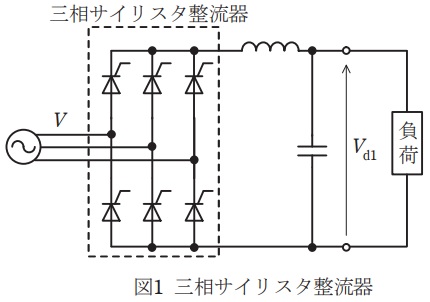
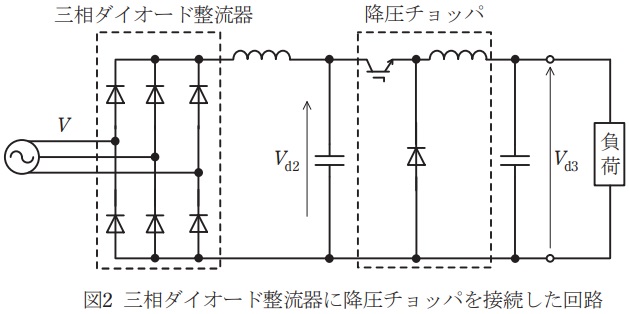
図1には三相サイリスタ整流器を，図2には三相ダイオード整流器に降圧チョッパを接続した回路を示す。ともに直流電源を得る回路である。交流電源は線間電圧実効値を\( \ V \ \)とする三相対称交流電源であり，電源のインピーダンス及びパワー半導体デバイスなどの回路要素のオン電圧，抵抗分は無視できるものとする。

三相サイリスタ整流器の出力直流電圧平均値\( \ V_{\mathrm {d1}} \ \)は，サイリスタの制御遅れ角を\( \ \alpha \ \mathrm {[rad]} \ \)とすると，次式となる。
\[
\begin{eqnarray}
V_{\mathrm {d1}} &=& \ \fbox {　 （１） 　} \ ・・・・・・・・・・・・・・・・・・・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] 正の電圧\( \ V_{\mathrm {d1}} \ \)は，制御遅れ角\( \ \alpha \ \)を\( \ \fbox {　 （２） 　} \ \)の範囲で制御することにより，変化させることができる。

一方，三相ダイオード整流器の出力直流電圧平均値\( \ V_{\mathrm {d2}} \ \)は，サイリスタとダイオードとのターンオン動作の違いから，①式において\( \ \alpha = \ \fbox {　 （３） 　} \ \mathrm {[rad]} \ \)としたときの電圧に等しい。交流電源の電圧に変動がなければ電圧\( \ V_{\mathrm {d2}} \ \)は\( \ \fbox {　 （４） 　} \ \)。さらに，後段の降圧チョッパの\( \ \fbox {　 （５） 　} \ \)を制御することにより，降圧チョッパの出力直流電圧平均値\( \ V_{\mathrm {d3}} \ \)を変化できる。\( \ \fbox {　 （５） 　} \ \)を\( \ d \ \)とすると，電圧\( \ V_{\mathrm {d3}} \ \)は次式となる。
\[
\begin{eqnarray}
V_{\mathrm {d3}} &=&d\cdot V_{\mathrm {d2}} \ \ ・・・・・・・・・・・・・・・・・・・・・・・・・・　② \\[ 5pt ] \end{eqnarray}
\] したがって，図1，図2のいずれの回路でも電圧制御ループを組むことにより，たとえ交流電源の電圧が変動したときでも，負荷の電圧を一定にできる。

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　効率　　　　　&（ロ）&　1.35V\cos \alpha　　　　　&（ハ）&　\pi ≦\alpha ≦2\pi \\[ 5pt ] &（ニ）&　通流率　　　　　&（ホ）&　0.9V\cos \alpha　　　　　&（ヘ）&　0.45V\cos \alpha \\[ 5pt ] &（ト）&　\frac {\pi }{3}　　　　　&（チ）&　\frac {\pi }{2}≦\alpha ≦\pi　　　　　　　&（リ）&　\frac {\pi }{6} \\[ 5pt ] &（ヌ）&　変調率　　　　　　　　　&（ル）&　一定である　　　　　&（ヲ）&　0 \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
&（ワ）&　0≦\alpha ≦\frac {\pi }{2}　　　&（カ）&　負荷電流に比例して増加する \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
&（ヨ）&　負荷電流に反比例して減少する \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

三相サイリスタブリッジ整流回路の動作に関する問題です。
二次試験では出力電圧の導出は必須となりますが，一次試験の場合はある程度覚えておく内容になるかと思います。理解している受験生の方が少ない問題と思いますので，ぜひ理解して他の受験生と差をつけるようにしましょう。

1.三相サイリスタブリッジ整流回路の動作
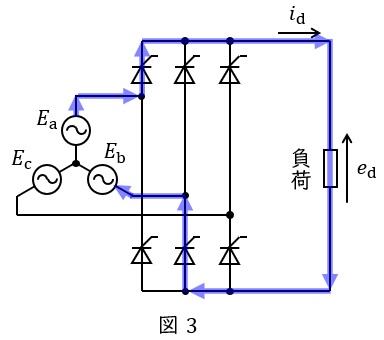
三相サイリスタブリッジ整流回路は図3のように\( \ 6 \ \)つのサイリスタを接続した回路で，サイリスタがオンするタイミングで一番電圧の高い相から一番電圧の低い相に電流が流れ，出力されます。
例えば\( \ E_{\mathrm {a}} \ \)が一番電圧が高く，\( \ E_{\mathrm {b}} \ \)が一番電圧が低い場合には図3に示すように電流が流れ\( \ e_{\mathrm {d}}=E_{\mathrm {a}}-E_{\mathrm {b}} \ \)が出力されます。
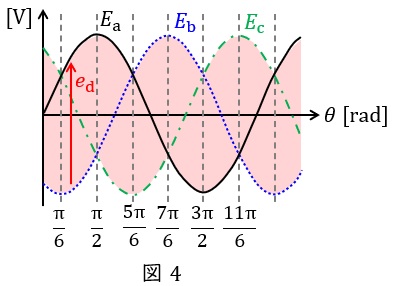
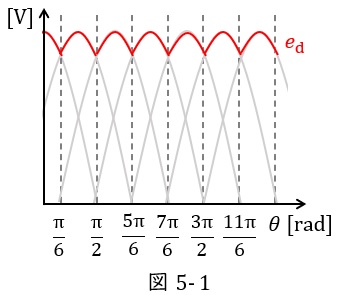
したがって，制御角\( \ \alpha =0 \ \)のときは図4に示した電圧\( \ e_{\mathrm {d}} \ \)が出力となり，電圧の波形の変化をまとめると図5-1のようになり，その平均電圧\( \ E_{\mathrm {d}} \ \)は基準電圧を\( \ E_{\mathrm {a}}=\sqrt {2}E\sin \omega t \ \)とすると，
\[
\begin{eqnarray}
E_{\mathrm {d}} &=&\frac {1}{\displaystyle \frac {\pi }{3}}\int _{\frac {\pi}{6}}^{\frac {\pi}{2}} \left( E_{\mathrm {a}}-E_{\mathrm {b}}\right) \mathrm {d}\omega t \\[ 5pt ] &=&\frac {3}{\pi }\int _{\frac {\pi}{6}}^{\frac {\pi}{2}} \left\{ \sqrt {2}E\sin \omega t-\sqrt {2}E\sin \left( \omega t-\frac {2}{3}\pi \right) \right\} \mathrm {d}\omega t \\[ 5pt ] \end{eqnarray}
\] となります。ここで和積の公式\( \ \displaystyle \sin A-\sin B=2\cos \frac {A+B}{2}\sin \frac {A-B}{2} \ \)より，
\[
\begin{eqnarray}
E_{\mathrm {d}} &=&\frac {3}{\pi }\int _{\frac {\pi}{6}}^{\frac {\pi}{2}} 2\sqrt {2}E \cos \left( \omega t-\frac {\pi}{3} \right)\sin \frac {\pi}{3} \mathrm {d}\omega t \\[ 5pt ] &=&\frac {3}{\pi }\int _{\frac {\pi}{6}}^{\frac {\pi}{2}} 2\sqrt {2}E \cos \left( \omega t-\frac {\pi}{3} \right) \frac {\sqrt {3}}{2}\mathrm {d}\omega t \\[ 5pt ] &=&\frac {3}{\pi }\int _{\frac {\pi}{6}}^{\frac {\pi}{2}} \sqrt {6}E \cos \left( \omega t-\frac {\pi}{3} \right) \mathrm {d}\omega t \\[ 5pt ] &=&\frac {3\sqrt {6}}{\pi }E\int _{\frac {\pi}{6}}^{\frac {\pi}{2}} \cos \left( \omega t-\frac {\pi}{3} \right) \mathrm {d}\omega t \\[ 5pt ] &=&\frac {3\sqrt {6}}{\pi }E\left[ \sin \left( \omega t-\frac {\pi}{3} \right) \right] _{\frac {\pi}{6}}^{\frac {\pi}{2}} \\[ 5pt ] &=&\frac {3\sqrt {6}}{\pi }E\left\{ \sin \left( \frac {\pi}{2}-\frac {\pi}{3} \right)- \sin \left( \frac {\pi}{6}-\frac {\pi}{3} \right)\right\} \\[ 5pt ] &=&\frac {3\sqrt {6}}{\pi }E\left\{ \sin \frac {\pi}{6}- \sin \left( -\frac {\pi}{6} \right)\right\} \\[ 5pt ] &=&\frac {3\sqrt {6}}{\pi }E\left\{ \frac {1}{2}- \left( -\frac {1}{2} \right)\right\} \\[ 5pt ] &=&\frac {3\sqrt {6}}{\pi }E \\[ 5pt ] \end{eqnarray}
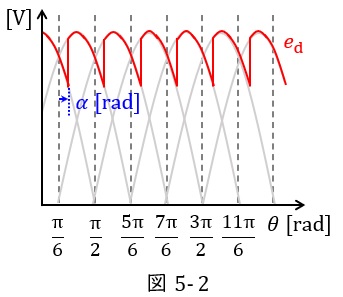
\] と求められます。同様に制御角\( \ \alpha ＞0 \ \)のときは図5-2に示すような出力電圧となり，
\[
\begin{eqnarray}
E_{\mathrm {d}} &=&\frac {1}{\displaystyle \frac {\pi }{3}}\int _{\frac {\pi}{6}+\alpha }^{\frac {\pi}{2}+\alpha } \left( E_{\mathrm {a}}-E_{\mathrm {b}}\right) \mathrm {d}\omega t \\[ 5pt ] &=&\frac {3}{\pi }\int _{\frac {\pi}{6}+\alpha }^{\frac {\pi}{2}+\alpha } \left\{ \sqrt {2}E\sin \omega t-\sqrt {2}E\sin \left( \omega t-\frac {2}{3}\pi \right) \right\} \mathrm {d}\omega t \\[ 5pt ] E_{\mathrm {d}} &=&\frac {3}{\pi }\int _{\frac {\pi}{6}+\alpha }^{\frac {\pi}{2}+\alpha } 2\sqrt {2}E \cos \left( \omega t-\frac {\pi}{3} \right)\sin \frac {\pi}{3} \mathrm {d}\omega t \\[ 5pt ] &=&\frac {3}{\pi }\int _{\frac {\pi}{6}+\alpha }^{\frac {\pi}{2}+\alpha } 2\sqrt {2}E \cos \left( \omega t-\frac {\pi}{3} \right) \frac {\sqrt {3}}{2}\mathrm {d}\omega t \\[ 5pt ] &=&\frac {3}{\pi }\int _{\frac {\pi}{6}+\alpha }^{\frac {\pi}{2}+\alpha } \sqrt {6}E \cos \left( \omega t-\frac {\pi}{3} \right) \mathrm {d}\omega t \\[ 5pt ] &=&\frac {3\sqrt {6}}{\pi }E\int _{\frac {\pi}{6}+\alpha }^{\frac {\pi}{2}+\alpha } \cos \left( \omega t-\frac {\pi}{3} \right) \mathrm {d}\omega t \\[ 5pt ] &=&\frac {3\sqrt {6}}{\pi }E\left[ \sin \left( \omega t-\frac {\pi}{3} \right) \right] _{\frac {\pi}{6}+\alpha }^{\frac {\pi}{2}+\alpha } \\[ 5pt ] &=&\frac {3\sqrt {6}}{\pi }E\left\{ \sin \left( \frac {\pi}{2}+\alpha -\frac {\pi}{3} \right)- \sin \left( \frac {\pi}{6}+\alpha -\frac {\pi}{3} \right)\right\} \\[ 5pt ] &=&\frac {3\sqrt {6}}{\pi }E\left\{ \sin \left( \alpha +\frac {\pi}{6} \right)- \sin \left( \alpha -\frac {\pi}{6} \right)\right\} \\[ 5pt ] &=&\frac {3\sqrt {6}}{\pi }E\cdot 2\cos \alpha \sin \frac {\pi }{6} \\[ 5pt ] &=&\frac {3\sqrt {6}}{\pi }E\cdot 2\cos \alpha \cdot \frac {1}{2} \\[ 5pt ] &=&\frac {3\sqrt {6}}{\pi }E\cos \alpha \\[ 5pt ] \end{eqnarray}
\] と求められます。

2.降圧チョッパの動作
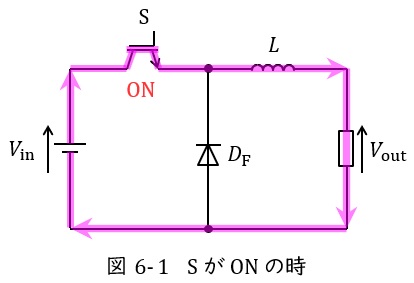
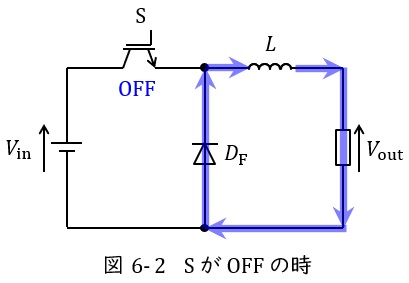
図6-1及び図6-2は降圧チョッパの例となります。
スイッチ\( \ \mathrm {S} \ \)がオンになると，図6-1のように電源からの電流はスイッチ\( \ \mathrm {S} \ \)を通り，リアクトル\( \ L \ \)側に電流が流れますが，ダイオード\( \ D_{\mathrm {F}} \ \)は逆向きなので電流が流れません。
スイッチ\( \ \mathrm {S} \ \)がオフになると，図6-2のように電源から電流は流れず，リアクトルに蓄えられているエネルギーから出力側と還流ダイオード\( \ D_{\mathrm {F}} \ \)に電流が流れます。
したがって降圧チョッパの出力電圧の平均値\( \ V_{\mathrm {out}} \ \)は，スイッチのオン時間を\( \ T_{\mathrm {on}} \ \)，オフ時間を\( \ T_{\mathrm {off}} \ \)とすると，
\[
\begin{eqnarray}
V_{\mathrm {out}}&=&\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}V_{\mathrm {in}} \\[ 5pt ] \end{eqnarray}
\] で求められます。このとき，\( \ V_{\mathrm {in}} \ \)の係数
\[
\begin{eqnarray}
\gamma &=&\frac {T_{\mathrm {ON}}}{T_{\mathrm {ON}}+T_{\mathrm {OFF}}} \\[ 5pt ] \end{eqnarray}
\] を通流率といいます。

【解答】

(1)解答：ロ
題意より解答候補は，（ロ）\( \ 1.35V\cos \alpha \ \)，（ホ）\( \ 0.9V\cos \alpha \ \)，（ヘ）\( \ 0.45V\cos \alpha \ \)，になると思います。
ワンポイント解説「1.三相サイリスタブリッジ整流回路の動作」の通り，出力直流電圧平均値\( \ V_{\mathrm {d1}} \ \)は，相電圧を\( \ E \ \)，線間電圧を\( \ V \ \)とすると，
\[
\begin{eqnarray}
V_{\mathrm {d1}} &=&\frac {3\sqrt {6}}{\pi }E\cos \alpha \\[ 5pt ] &=&\frac {3\sqrt {2}}{\pi }V\cos \alpha \\[ 5pt ] &≒&1.35V\cos \alpha \\[ 5pt ] \end{eqnarray}
\] で求められます。

(2)解答：ワ
題意より解答候補は，（ハ）\( \ \displaystyle \pi ≦\alpha ≦2\pi \ \)，（チ）\( \ \displaystyle \frac {\pi }{2}≦\alpha ≦\pi \ \)，（ワ）\( \ \displaystyle 0≦\alpha ≦\frac {\pi }{2} \ \)，になると思います。
ワンポイント解説「1.三相サイリスタブリッジ整流回路の動作」の通り，\( \ V_{\mathrm {d1}}≒1.35V\cos \alpha \ \)であるため，正の電圧を得るためには\( \ \displaystyle 0≦\alpha ≦\frac {\pi }{2} \ \)で制御する必要があります。

(3)解答：ヲ
題意より解答候補は，（ト）\( \ \displaystyle \frac {\pi }{3} \ \)，（リ）\( \ \displaystyle \frac {\pi }{6} \ \)，（ヲ）\( \ \displaystyle 0 \ \)，になると思います。
ワンポイント解説「1.三相サイリスタブリッジ整流回路の動作」の通り，制御遅れ角\( \ \alpha = 0 \ \mathrm {[rad]} \ \)としたとき，三相ダイオードブリッジ整流器の電圧に等しくなります。

(4)解答：ル
題意より解答候補は，（ル）一定である，（カ）負荷電流に比例して増加する，（ヨ）負荷電流に反比例して減少する，になると思います。
ワンポイント解説「1.三相サイリスタブリッジ整流回路の動作」の通り，\( \ V_{\mathrm {d2}}≒1.35V\cos \alpha \ \)は負荷電流に関係なく一定であることがわかります。

(5)解答：ニ
題意より解答候補は（イ）効率，（ニ）通流率，（ヌ）変調率，になると思います。
ワンポイント解説「2.降圧チョッパの動作」の通り，出力電圧を調整することができる\( \ d \ \)を通流率といいます。