《電力》〈送電〉[H19:問7]CVケーブルに発生する損失に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

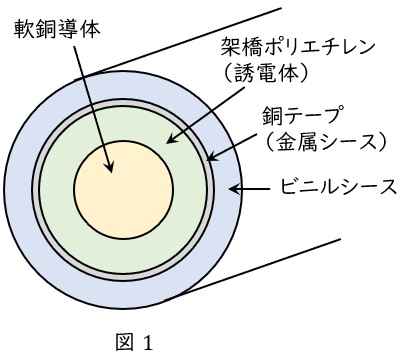
次の文章は，電力用$ \ \mathrm {CV} \ $ケーブルに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる語句を解答群の中から選び，その記号をマークシートに記入しなさい。

電力用$ \ \mathrm {CV} \ $ケーブルの充電電流が大きくなると，送電容量に影響を与えることから，設計に際して考慮が必要である。充電電流は単位長当たりのケーブル静電容量，$ \ \fbox {　（１）　} \ $及び線路長に比例して大きくなる。ケーブル導体サイズが同じであれば，単位長当たりのケーブル静電容量は，絶縁体の誘電率が大きいほど，また，$ \ \fbox {　（２）　} \ $が小さいほど大きい。

$ \ \mathrm {CV} \ $ケーブルの$ \ \fbox {　（３）　} \ $損失も送電容量に影響を与える。これは，充電電流にいくらかの有効成分があるために発生する損失であり，送電電圧が同じ場合，$ \ \fbox {　（４）　} \ $の大きいものほど発生量が大きい。

また，$ \ \fbox {　（５）　} \ $を鉄管に入線すると鉄損が大きくなることから，送電容量を低下させることになるので注意が必要である。

〔問7の解答群〕
\[
\begin{eqnarray}
&（イ）&　無効電力　　　　　&（ロ）&　埋設深さ　　　　　&（ハ）&　許容電流 \\[ 5pt ] &（ニ）&　単心ケーブル　　　　　　　&（ホ）&　誘電体　　　　　&（ヘ）&　送電電圧 \\[ 5pt ] &（ト）&　熱抵抗　　　　　&（チ）&　絶縁体厚さ　　　　　　　&（リ）&　三心ケーブル \\[ 5pt ] &（ヌ）&　シース厚さ　　　　　&（ル）&　銅　　　　　&（ヲ）&　がい装厚さ \\[ 5pt ] &（ワ）&　送電電流　　　　　&（カ）&　誘電正接　　　　　&（ヨ）&　トリプレックス型ケーブル \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

電力用$ \ \mathrm {CV} \ $ケーブルに発生する損失に関する問題です。
ケーブルは金属と誘電体等が何層にもなった構造をしており，各部で損失が発生します。
解説では原理や計算等も含め説明していますが，試験本番においてはある程度頭に入れて解いていく必要があると考えて下さい。

1.ケーブルに発生する損失
①抵抗損
導体部の抵抗により発生する損失で，導体電流の$ \ 2 \ $乗に比例します。

②誘電体損
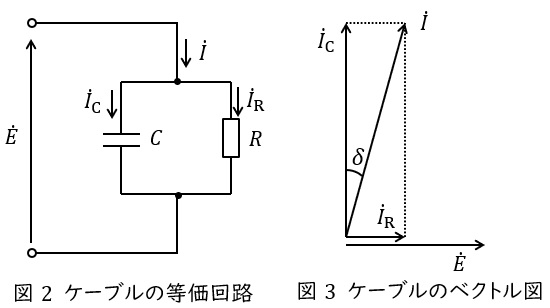
ケーブルの絶縁体部に流れる電流のうち，抵抗成分に流れる電流による損失です。ケーブルは誘電体を金属で挟んだコンデンサのような構造をしているため，損失分も合わせ一相分等価回路は図2のように抵抗$ \ R \ \mathrm {[\Omega ]} \ $と静電容量$ \ C \ \mathrm {[F]} \ $の並列回路となり，図3のベクトル図に示すような電流が流れます。ただし，$ \ \dot E \ \mathrm {[V]} \ $はケーブルに加わる電圧の相電圧となります。
この時のコンデンサ分に流れる電流$ \ I_{\mathrm {C}} \ \mathrm {[A]} \ $に対する抵抗分に流れる電流$ \ I_{\mathrm {R}} \ \mathrm {[A]} \ $の割合$ \ \displaystyle \frac {I_{\mathrm {R}}}{I_{\mathrm {C}}}=\tan \delta \ $を誘電正接と呼び，ケーブルが劣化してくると大きくなります。
ケーブルの誘電体損$ \ W_{\mathrm {d}} \ \mathrm {[W]} \ $は，ケーブルに加わる電圧（線間電圧）を$ \ V \ \mathrm {[V]} \ $，周波数を$ \ f \ \mathrm {[Hz]} \ $，角周波数を$ \ \omega =2\pi f \ \mathrm {[rad / s]} \ $とすると，
\[
\begin{eqnarray}
W_{\mathrm {d}}&=&3\frac {V}{\sqrt {3}}I_{\mathrm {R}} \\[ 5pt ] &=&3\frac {V}{\sqrt {3}}I_{\mathrm {C}}\tan \delta \\[ 5pt ] &=&3\frac {V}{\sqrt {3}}\left( \omega C\frac {V}{\sqrt {3}}\right) \tan \delta \\[ 5pt ] &=&\omega CV^{2}\tan \delta \\[ 5pt ] &=&2\pi f CV^{2}\tan \delta \\[ 5pt ] \end{eqnarray}
\] となり，誘電体損は電圧$ \ V \ \mathrm {[V]} \ $の$ \ 2 \ $乗に比例し，周波数$ \ f \ \mathrm {[Hz]} \ $，誘電正接$ \ \tan \delta \ $に比例することがわかります。

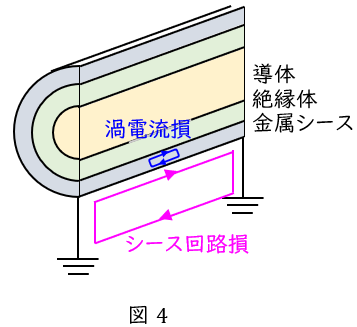
③シース損
ケーブルの絶縁体部の外側に巻く金属（シース）に発生する損失で，図4に示すようにシースを流れる循環電流によるシース回路損と渦電流による渦電流損があります。ケーブル導体を流れる電流から発生する磁束により電圧が誘起され損失が発生します。

【解答】

(1)解答：ヘ
題意より，解答候補は（イ）無効電力，（ロ）埋設深さ，（ハ）許容電流，（ヘ）送電電圧，（ト）熱抵抗，（チ）絶縁体厚さ，（ヌ）シース厚さ，（ヲ）がい装厚さ，（ワ）送電電流，（カ）誘電正接，になると思います。
ワンポイント解説「1.ケーブルに発生する損失」②誘電体損の図2の通り，充電電流$ \ I_{\mathrm {C}} \ \mathrm {[A]} \ $は，$ \ \displaystyle I_{\mathrm {C}}=2\pi f C\frac {V}{\sqrt {3}} \ \mathrm {[A]} \ $となるので，送電電圧$ \ V \ \mathrm {[V]} \ $に比例して大きくなります。

(2)解答：チ
題意より，解答候補は（イ）無効電力，（ロ）埋設深さ，（ハ）許容電流，（ヘ）送電電圧，（ト）熱抵抗，（チ）絶縁体厚さ，（ヌ）シース厚さ，（ヲ）がい装厚さ，（ワ）送電電流，（カ）誘電正接，になると思います。
平行平板コンデンサの静電容量の公式$ \ \displaystyle C=\frac {\varepsilon S}{d} \ $より，単位長当たりのケーブル静電容量は，絶縁体の誘電率$ \ \varepsilon \ $が大きいほど，絶縁体厚さ$ \ d \ $が小さいほど大きくなります。

(3)解答：ホ
題意より，解答候補は（イ）無効電力，（ホ）誘電体，（ト）熱抵抗，（ル）銅，になると思います。
ワンポイント解説「1.ケーブルに発生する損失」②誘電体損の通り，充電電流にいくらかの有効成分があるために発生する損失は誘電体損失といい，送電容量に影響を与えます。

(4)解答：カ
題意より，解答候補は（イ）無効電力，（ロ）埋設深さ，（ハ）許容電流，（ヘ）送電電圧，（ト）熱抵抗，（チ）絶縁体厚さ，（ヌ）シース厚さ，（ヲ）がい装厚さ，（ワ）送電電流，（カ）誘電正接，になると思います。
ワンポイント解説「1.ケーブルに発生する損失」②誘電体損の通り，誘電体損失$ \ W_{\mathrm {d}} \ \mathrm {[W]} \ $は，$ \ W_{\mathrm {d}} =2\pi f CV^{2}\tan \delta \ \mathrm {[W]} \ $となるので，送電電圧が同じ場合，誘電正接$ \ \tan \delta \ $の大きいものほど発生量が大きくなります。

(5)解答：ニ
題意より，解答候補は（ニ）単心ケーブル，（リ）三心ケーブル，（ヨ）トリプレックス型ケーブル，になると思います。
ワンポイント解説「1.ケーブルに発生する損失」③シース損の通り，ケーブルのシースを流れるシース損と同様に単心ケーブルを鉄管に入線すると鉄損が大きくなります。三心ケーブルやトリプレックス型ケーブルであれば三相合計の電流が零となり，発生する磁束が打ち消し合うため鉄損はあまり大きくなりません。