《機械》〈回転機〉[H26:問1]直流機の整流作用に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，直流機の整流作用に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。

直流機では電機子巻線によって発生する交流を整流子によって直流に変えることを整流作用という。電機子が回転すると，隣り合った二つの整流子片がブラシで$ \ \fbox {　（１）　} \ $される状態が生じ，その都度コイルの電流$ \ I_{\mathrm {C}} \ $はその方向を反転する。いま，回転している整流子の周辺速度を$ \ v_{\mathrm {C}} \ \mathrm {[ m ／ s ]} \ $，ブラシの幅を$ \ b \ \mathrm {[ m ]} \ $，整流子間の絶縁マイカの厚さを$ \ \delta \ \mathrm {[ m ]} \ $とすれば，整流時間(整流周期)$ \ T_{\mathrm {C}} \ \mathrm {[ s ]} \ $は次式で与えられる。
\[
T_{\mathrm {C}}=\fbox {　（２）　}
\] 主にコイルの自己インダクタンスによって，整流中に電流の反転による電流変化に応じてコイルの誘導起電力が生じる。これを$ \ \fbox {　（３）　} \ $という。

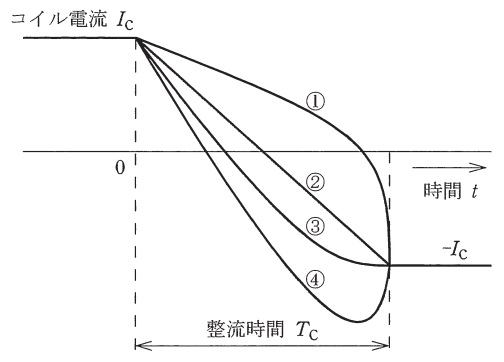
整流時間$ \ T_{\mathrm {C}} \ $におけるコイル内の電流変化を示した図を整流曲線といい，主な曲線例を図に示す。図中②は$ \ \fbox {　（４）　} \ $整流といい，ブラシと整流子片間の電流が接触面積に比例する場合で電流変化の基準となるものである。①は電流の変化が遅く整流の終わり近くで電流が急変するので，$ \ \fbox {　（３）　} \ $が発生し，ブラシの後端から火花を発生しやすい。④は電流の変化が速すぎ，過整流という。③は整流終了時の電流変化が小さく火花の発生を防ぐことができる。

良好な整流が得られないと整流子面の火花が激しくなり，整流子面を損傷させ，ブラシの摩耗を早めることになる。その対策として，主磁極間の幾何学的中性軸の位置に$ \ \fbox {　（５）　} \ $を取り付け，$ \ \fbox {　（３）　} \ $を打ち消す方向に電圧を誘導して，良好な整流を得ることができる。これを電圧整流という。

〔問1の解答群〕
\[
\begin{eqnarray}
&（イ）&　直　線　　　　　&（ロ）&　補償巻線　　　　　&（ハ）&　補　極 \\[ 5pt ] &（ニ）&　短　絡　　　　　&（ホ）&　整流起電力　　　　　&（ヘ）&　\frac {b+\delta }{v_{\mathrm {C}}} \\[ 5pt ] &（ト）&　\frac {\delta -b}{v_{\mathrm {C}}}　　　　　&（チ）&　電機子反作用　　　　　　&（リ）&　リアクタンス電圧 \\[ 5pt ] &（ヌ）&　開　放　　　　&（ル）&　減　速　　　　　&（ヲ）&　臨　界 \\[ 5pt ] &（ワ）&　\frac {b-\delta }{v_{\mathrm {C}}}　　　　　&（カ）&　比　例　　　　　&（ヨ）&　整流子 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

この年は問1からかなり難しめの問題で私も構造はメーカーの仕様書でしか見たことがありません。直流機の整流に関する非常に細かい箇所の問題で，三種ではまず出題されないレベルの問題と言えると思います。メカニズムを理解する上では良い問題となりますので，理解しておくようにしておきましょう。

【解答】

(1)解答：ニ
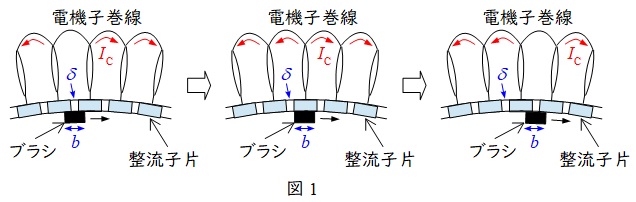
ブラシと整流子片のメカニズムを図1に示します。電機子が回転すると，隣り合った整流子片がブラシで短絡される状態が生じ，短絡する毎にコイルの電流$ \ I_{\mathrm {C}} \ $が反転します。

(2)解答：ワ
図1より，回転している整流子の周辺速度$ \ v_{\mathrm {C}} \ $とすると，短絡している時間(整流時間)$ \ T_{\mathrm {C}} \ $は，
\[
T_{\mathrm {C}}=\frac {b-\delta }{v_{\mathrm {C}}}
\] と求められる。

(3)解答：リ
コイル自身のインダクタンスによって，整流中の電流の反転による電流変化に応じてコイルに誘導起電力が生じることをリアクタンス電圧と言います。

(4)解答：イ
問題図の②は直線整流といい，整流としては最も理想的な整流となります。一方，①のような整流終わりに急激に変化する整流を不足整流，④のように電流の変化が早すぎる場合を過整流と言います。

(5)解答：ハ
主磁極間の幾何学的中性軸に取り付けるのは補極で，幾何学的中性軸以外の電機子反作用には補償巻線が用いられます。