参考書解説の不明点について教えて下さい。

【質問】

【回答】

ご質問ありがとうございました。
もし，この問題の解説で四端子定数の定義や電力の導出を説明されていないのであれば，解説書としては不十分であると言わざるを得ません。
電力と電圧から電流を求める時，共役複素数を取る必要があり，それにより，\({\dot I}_{\mathrm {r}}\)の式で複素数部分の符号が入れ替わることになります。
以下，私なりの解答を例示しますのでご参考になさって頂ければ幸いです。

送電端相電圧を\({\dot E}_{\mathrm {s}}\)，送電端電流を\({\dot I}_{\mathrm {s}}\)，受電端相電圧を\({\dot E}_{\mathrm {r}}\)，受電端電流を\({\dot I}_{\mathrm {r}}\)とすると，
\[
\begin{pmatrix} {\dot E}_{\mathrm {s}} \\ {\dot I}_{\mathrm {s}} \end{pmatrix} = \begin{pmatrix} \dot A & \dot B \\ \dot C & \dot D \end{pmatrix} \begin{pmatrix} {\dot E}_{\mathrm {r}} \\ {\dot I}_{\mathrm {r}} \end{pmatrix}
\] と表すことができる。
受電端負荷の有効電力が\(P=21 \ \mathrm {MW}\)であるから，無効電力\(Q\)は，
\[
\begin{eqnarray}
Q&=& \frac {P}{\cos \theta } \cdot \sin \theta \\[ 5pt ] &=&\frac {\sqrt {1-\cos ^{2}\theta }}{\cos \theta } P \\[ 5pt ]　
&=&\frac {\sqrt {1-0.8^{2}}}{0.8} \times 21 \\[ 5pt ]　　
&=&15.75 \ \mathrm {[Mvar]}
\end{eqnarray}
\] である。受電端電圧を基準として，遅れ無効電力を正とすると，
\[
\begin{eqnarray}
P+jQ&=&\sqrt {3}{\dot V}_{\mathrm {r}}\overline {\dot I}_{\mathrm {r}} \\[ 5pt ] \end{eqnarray}
\] であるから，受電端電流\({\dot I}_{\mathrm {r}}\)は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {r}}&=&\frac {\overline {P+jQ}}{\sqrt {3}\overline {{\dot V}_{\mathrm {r}}}} \\[ 5pt ] &=&\frac {P-jQ}{\sqrt {3}\overline {{\dot V}_{\mathrm {r}}}} \\[ 5pt ] &=&\frac {21\times 10^{6} -j15.75 \times 10^{6}}{\sqrt {3}\times 100\times 10^{3}} \\[ 5pt ] &=&\frac {1}{\sqrt {3}}\left( 210 -j157.5 \right) \ \mathrm {[A]} \\[ 5pt ] &=&\frac {1}{\sqrt {3}}\left( 0.210 -j0.1575 \right) \ \mathrm {[kA]}
\end{eqnarray}
\] と求められる。この計算結果と四端子定数より，送電端相電圧\({\dot E}_{\mathrm {s}}\)は，
\[
\begin{eqnarray}
{\dot E}_{\mathrm {s}} &=&\dot A {\dot E}_{\mathrm {r}}+\dot B {\dot I}_{\mathrm {r}} \\[ 5pt ] &=&0.98 \times \frac {100}{\sqrt {3}} +j70.7 \times \frac {1}{\sqrt {3}}\left( 0.210 -j0.1575 \right) \\[ 5pt ] &≒&\frac {1}{\sqrt {3}} \left( 98 +j14.847 +11.135 \right) \\[ 5pt ] &≒&\frac {1}{\sqrt {3}} \left( 109.14 +j14.847 \right) \ \mathrm {[kV]} \\[ 5pt ] \end{eqnarray}
\] となるので，送電端電圧\({\dot V}_{\mathrm {s}}\)の大きさは，
\[
\begin{eqnarray}
\left| {\dot V}_{\mathrm {s}} \right| &=&\left| \sqrt {3}{\dot E}_{\mathrm {s}} \right| \\[ 5pt ] &=&\left| \sqrt {3}\times \frac {1}{\sqrt {3}} \left( 109.14 +j14.847 \right) \right| \\[ 5pt ] &=&\left| 109.14 +j14.847 \right| \\[ 5pt ] &=&\sqrt {109.14^{2}+14.847^{2}} \\[ 5pt ] &≒&110.15　→　110 \ \mathrm {[kV]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

【参考】

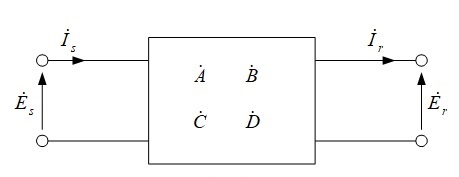
1.四端子定数
任意の下図のような回路がある時，送電端の相電圧\({\dot E}_{\mathrm {s}}\)と電流\({\dot I}_{\mathrm {s}}\)，受電端の相電圧\({\dot E}_{\mathrm {r}}\)と電流\({\dot I}_{\mathrm {r}}\)の関係が以下の行列式で表されるものを四端子定数と言います。
\[
\begin{pmatrix} {\dot E}_{\mathrm {s}} \\ {\dot I}_{\mathrm {s}} \end{pmatrix} = \begin{pmatrix} \dot A & \dot B \\ \dot C & \dot D \end{pmatrix} \begin{pmatrix} {\dot E}_{\mathrm {r}} \\ {\dot I}_{\mathrm {r}} \end{pmatrix}
\] ただし，
\[
\begin{eqnarray}
\dot A&=&\left. \frac {{\dot E}_{\mathrm {s}}}{{\dot E}_{\mathrm {r}}} \right| _{{\dot I}_{\mathrm {r}}=0}　　　
\dot B&=&\left. \frac {{\dot E}_{\mathrm {s}}}{{\dot I}_{\mathrm {r}}} \right| _{{\dot E}_{\mathrm {r}}=0} \\[ 5pt ] \dot C&=&\left. \frac {{\dot I}_{\mathrm {s}}}{{\dot E}_{\mathrm {r}}} \right| _{{\dot I}_{\mathrm {r}}=0}　　　
\dot D&=&\left. \frac {{\dot I}_{\mathrm {s}}}{{\dot I}_{\mathrm {r}}} \right| _{{\dot E}_{\mathrm {r}}=0}
\end{eqnarray}
\] となります。