《電力》〈火力〉[R01:問5]ガスタービン発電の熱サイクルに関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，ガスタービン発電の熱サイクルに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

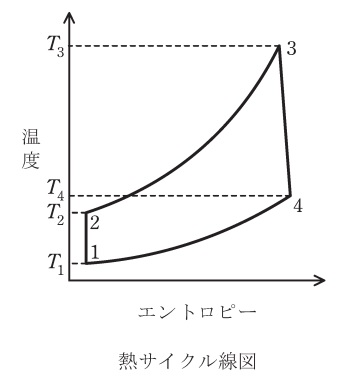
燃焼器が$ \ 1 \ $組だけのガスタービン発電における基本熱サイクルを単純$ \ \fbox {　（１）　} \ $といい，基本設備は燃焼器のほかに発電機，$ \ \fbox {　（２）　} \ $，ガスタービンで構成される。図は単純$ \ \fbox {　（１）　} \ $の熱サイクル線図で，燃焼器に相当する軌跡は$ \ \fbox {　（３）　} \ $である。燃焼器で発生した高温高圧の燃焼ガスをガスタービンで$ \ \fbox {　（４）　} \ $させタービン軸を回し仕事をする。受熱量を$ \ Q_{1} \ $，放熱量を$ \ Q_{2} \ $，各点の温度を$ \ T_{1} \ $，$ \ T_{2} \ $，$ \ T_{3} \ $，$ \ T_{4} \ $とすれば，理論熱効率$ \ \eta \ $は次式で示される。
\[
\begin{eqnarray}
\eta &=&1-\frac {Q_{2}}{Q_{1}} \\[ 5pt ] &=&1-\fbox {　（５）　} \\[ 5pt ] \end{eqnarray}
\]

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　ブレイトンサイクル　　　　　　　&（ロ）&　1 \ から \ 2　　　　　&（ハ）&　排熱回収ボイラ \\[ 5pt ] &（ニ）&　カルノーサイクル　　　　　&（ホ）&　断熱膨張　　　　　&（ヘ）&　\frac {T_{1}}{T_{3}} \\[ 5pt ] &（ト）&　2 \ から \ 3　　　　　&（チ）&　4 \ から \ 3　　　　　&（リ）&　空気圧縮機 \\[ 5pt ] &（ヌ）&　等圧燃焼　　　　　&（ル）&　ランキンサイクル　　　　　&（ヲ）&　断熱圧縮 \\[ 5pt ] &（ワ）&　脱硝装置　　　　　&（カ）&　\frac {T_{2}-T_{1}}{T_{3}-T_{4}}　　　　　&（ヨ）&　\frac {T_{4}-T_{1}}{T_{3}-T_{2}} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

ガスタービンに関する問題です。近年ではガスタービンと蒸気タービンを組み合わせたコンバインドサイクル発電の問題の方が圧倒的に多いです。本問はガスタービンのみを深堀りしたような内容となっているので，電験の問題としては特殊な問題と言えると思います。

1.ガスタービン発電
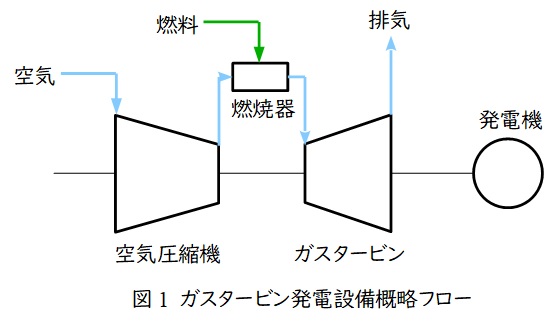
図1にガスタービン発電の概略フローを示します。
空気圧縮機で圧縮した空気に燃料ガスを噴射して燃焼し，燃焼した高温高圧ガスをガスタービンに送ることで発電します。
図1において，空気圧縮機が断熱圧縮（熱サイクルの$ \ 1 \ $→$ \ 2 \ $），燃焼器が等圧加熱（熱サイクルの$ \ 2 \ $→$ \ 3 \ $），ガスタービンが断熱膨張（熱サイクルの$ \ 3 \ $→$ \ 4 \ $）となります。
ガスタービンの特徴としては構造が簡単であり，起動停止が早く，運転操作も容易ですが，熱効率が$ \ 20～30 \ \mathrm {％} \ $程度と低いため，予備電源や非常用電源として使用されることが多いです。

【解答】

(1)解答：イ
題意より，解答候補は（イ）ブレイトンサイクル，（ニ）カルノーサイクル，（ル）ランキンサイクル，になると思います。ガスタービンに該当するのはブレイトンサイクルと呼ばれます。カルノーサイクルは理想のサイクルと呼ばれているサイクルで，ランキンサイクルは一般の汽力発電のサイクルとなります。

(2)解答：リ
題意より，解答候補は（ハ）排熱回収ボイラ，（リ）空気圧縮機，（ワ）脱硝装置，になると思います。ワンポイント解説「1.ガスタービン発電」の通り，ガスタービン発電に該当するのは空気圧縮機となります。

(3)解答：ト
題意より，解答候補は（ロ）$ \ 1 \ $から$ \ 2 \ $，（ト）$ \ 2 \ $から$ \ 3 \ $，（チ）$ \ 4 \ $から$ \ 3 \ $，になると思います。ワンポイント解説「1.ガスタービン発電」の通り，燃焼器に相当する軌跡は（ト）$ \ 2 \ $から$ \ 3 \ $となります。（エントロピーより温度を見た方がわかりやすいと思います。

(4)解答：ホ
題意より，解答候補は（ホ）断熱膨張，（ヌ）等圧燃焼，（ヲ）断熱圧縮，になると思います。ガスタービンでは燃焼ガスを断熱膨張させることでタービンを回転させます。

(5)解答：ヨ
空気の定圧熱容量を$ \ C_{\mathrm {p}} \ $とすると，
\[
\begin{eqnarray}
Q &=&C_{\mathrm {p}}\Delta T \\[ 5pt ] \end{eqnarray}
\] の関係があるので，受熱量$ \ Q_{1} \ $は，
\[
\begin{eqnarray}
Q_{1} &=&C_{\mathrm {p}}\left( T_{3}-T_{2}\right) \\[ 5pt ] \end{eqnarray}
\] となり，放熱量$ \ Q_{2} \ $は，
\[
\begin{eqnarray}
Q_{2} &=&C_{\mathrm {p}}\left( T_{4}-T_{1}\right) \\[ 5pt ] \end{eqnarray}
\] となる。したがって，理論熱効率$ \ \eta \ $は，
\[
\begin{eqnarray}
\eta &=&1-\frac {Q_{2}}{Q_{1}} \\[ 5pt ] &=&1-\frac {C_{\mathrm {p}}\left( T_{4}-T_{1}\right) }{C_{\mathrm {p}}\left( T_{3}-T_{2}\right) } \\[ 5pt ] &=&1-\frac {T_{4}-T_{1}}{T_{3}-T_{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。