【問題】
【難易度】★★★★★(難しい)
次の文章は,ユニット多重インバータの主回路構成,波形及び用途に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。
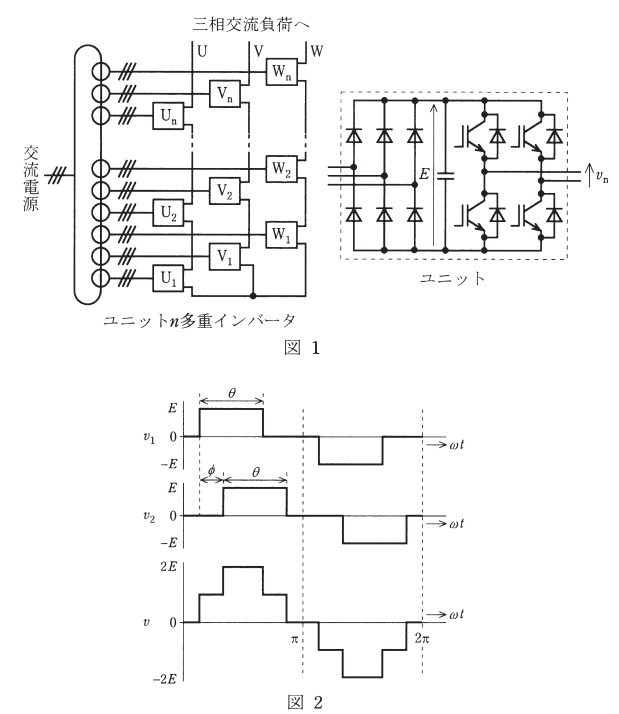
図1は,ユニット\( \ n \ \)多重インバータ及びその個々のユニットの主回路構成を示す。ユニットには\( \ \fbox { (1) } \ \)が含まれ,ユニット\( \ n \ \)多重インバータの\( \ \mathrm {Y} \ \)結線三相出力の各相には\( \ n \ \)段のユニットが直列接続される。直列接続されたユニットの\( \ \fbox { (2) } \ \)ために,入力側は変圧器の別巻線に接続している。また,ダイオードブリッジ整流器が出力する直流電圧はほぼ一定であるが,スイッチング回数が最少である\( \ \fbox { (3) } \ \)制御によって出力の交流電圧を制御することができる。
以下に\( \ n=2 \ \)の場合を考える。図2は,そのときの出力電圧の合成の様子を示す。\( \ \mathrm {PWM} \ \)制御を用いなくても,複数の電圧ステップがあるので,高調波電圧を低減することができる。例えば,\( \ 5 \ \)次高調波を除去するためには,二つの電圧の位相差を\( \ \phi \ \)とすると,
\[
\begin{eqnarray}
\sin 5 \omega t +\sin 5\left( \omega t-\phi \right) &=&0 \\[ 5pt ]
\end{eqnarray}
\]
の関係があればよい。\( \ 7 \ \)次高調波に対しても同様のことがいえる。したがって,それらの間の値\( \ \phi = \fbox { (4) } \ \)を選ぶと,\( \ 5 \ \)次及び\( \ 7 \ \)次高調波を零にはできないが,大幅に減らすことができる。一方,\( \ n=2 \ \)としたユニット\( \ 2 \ \)多重インバータのこのときの基本波電圧の大きさは,一つのユニットが出力する基本波電圧の大きさの\( \ \fbox { (5) } \ \)電圧となる。
この回路構成では直列のユニット段数\( \ n \ \)を大きくすることによって出力電圧を高くすることができる。したがって,\( \ 3.3 \ \mathrm {[kV]} \ \),\( \ 6.6 \ \mathrm {[kV]} \ \)などの高圧商用交流電源で駆動されている電動機を可変速化して省エネルギー運転する用途に使用されることが多い。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& 2 \ 倍を超える &(ロ)& 間を絶縁する &(ハ)& \frac {\pi }{12} \ \mathrm {[rad]} \\[ 5pt ]
&(ニ)& パルス幅 &(ホ)& \frac {\pi }{3} \ \mathrm {[rad]} &(ヘ)& 2 \ 倍の \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
&(ト)& 三相ダイオードブリッジ整流器及び三相インバータ \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
&(チ)& 間で電流分担する &(リ)& パルス振幅 &(ヌ)& 間で循環電流を流す \\[ 5pt ]
&(ル)& 2 \ 倍未満の &(ヲ)& \frac {\pi }{6} \ \mathrm {[rad]} &(ワ)& パルス周波数 \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
&(カ)& 三相ダイオードブリッジ整流器及び単相インバータ \\[ 5pt ]
&(ヨ)& 単相ダイオードブリッジ整流器及び三相インバータ \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
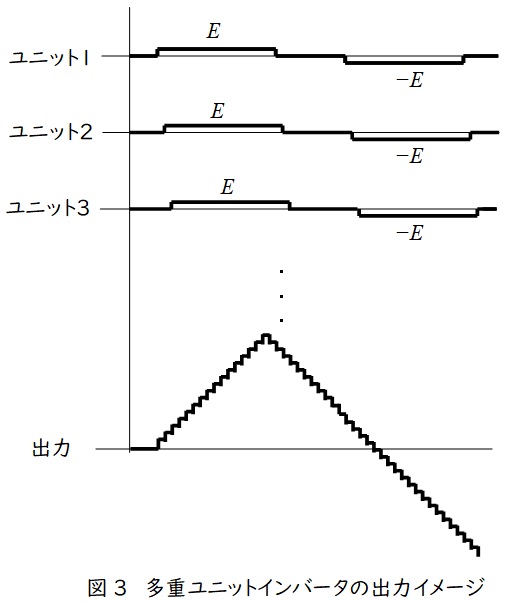
多重ユニットインバータはインバータの素子ユニットを直列に接続することで高電圧を得る方法で,個々の電流はほぼ一定に近い波形ですが,ユニット間の位相角を調整することで下図のように,正弦波交流とはいかないですが,交流出力を得ることができます。素子の耐電圧より大きい大型機で活躍します。
1.三角関数の和積の公式
三角関数の加法定理は,
\[
\begin{eqnarray}
\sin \left( \alpha + \beta \right) &=&\sin \alpha \cos \beta +\cos \alpha \sin \beta &・・・・①& \\[ 5pt ]
\sin \left( \alpha – \beta \right) &=&\sin \alpha \cos \beta -\cos \alpha \sin \beta &・・・・②& \\[ 5pt ]
\cos \left( \alpha + \beta \right) &=&\cos \alpha \cos \beta -\sin \alpha \sin \beta &・・・・③& \\[ 5pt ]
\cos \left( \alpha – \beta \right) &=&\cos \alpha \cos \beta +\sin \alpha \sin \beta &・・・・④& \\[ 5pt ]
\end{eqnarray}
\]
であるから,\(①+②\)より,
\[
\begin{eqnarray}
\sin \left( \alpha + \beta \right) +\sin \left( \alpha – \beta \right) &=&2\sin \alpha \cos \beta &・・・・⑤& \\[ 5pt ]
\end{eqnarray}
\]
\(①-②\)より,
\[
\begin{eqnarray}
\sin \left( \alpha + \beta \right) -\sin \left( \alpha – \beta \right) &=&2\cos \alpha \sin \beta &・・・・⑥& \\[ 5pt ]
\end{eqnarray}
\]
\(③+④\)より,
\[
\begin{eqnarray}
\cos \left( \alpha + \beta \right) +\cos \left( \alpha – \beta \right) &=&2\cos \alpha \cos \beta &・・・・⑦& \\[ 5pt ]
\end{eqnarray}
\]
\(③-④\)より,
\[
\begin{eqnarray}
\cos \left( \alpha + \beta \right) -\cos \left( \alpha – \beta \right) &=&-2\sin \alpha \sin \beta &・・・・⑧& \\[ 5pt ]
\end{eqnarray}
\]
となります。\( \ \alpha + \beta =A \ \),\( \ \alpha – \beta =B \ \)とすると,\( \ \displaystyle \alpha =\frac {A+B}{2} \ \),\( \ \displaystyle \beta =\frac {A-B}{2} \ \)であるから,\( \ ⑤~⑧ \ \)に代入すると,
\[
\begin{eqnarray}
\sin A +\sin B &=&2\sin \frac {A+B}{2} \cos \frac {A-B}{2} \\[ 5pt ]
\sin A -\sin B &=&2\cos \frac {A+B}{2} \sin \frac {A-B}{2} \\[ 5pt ]
\cos A +\cos B &=&2\cos \frac {A+B}{2} \cos \frac {A-B}{2} \\[ 5pt ]
\cos A -\cos B &=&-2\sin \frac {A+B}{2} \sin \frac {A-B}{2} \\[ 5pt ]
\end{eqnarray}
\]
と和積の公式が求められます。
【関連する「電気の神髄」記事】
【解答】
(1)解答:カ
題意より解答候補は,(ト)三相ダイオードブリッジ整流器及び三相インバータ,(カ)三相ダイオードブリッジ整流器及び単相インバータ,(ヨ)単相ダイオードブリッジ整流器及び三相インバータ,になると思います。下図の通り,ユニットは三相ダイオードブリッジと単相インバータから構成されています。
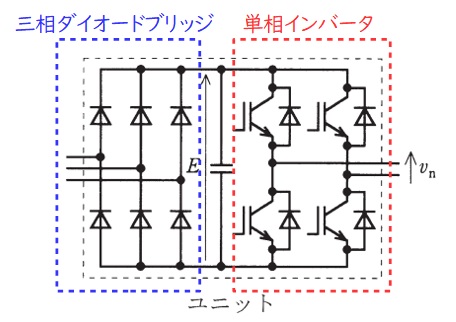
(2)解答:ロ
題意より解答候補は,(ロ)間を絶縁する,(チ)間で電流分担する黄,(ヌ)間で循環電流を流す,になると思います。下図のように,入力側の変圧器の巻線を同じにすると短絡回路が形成されてしまうので,ユニットの間を絶縁するために入力側は別巻線に接続します。
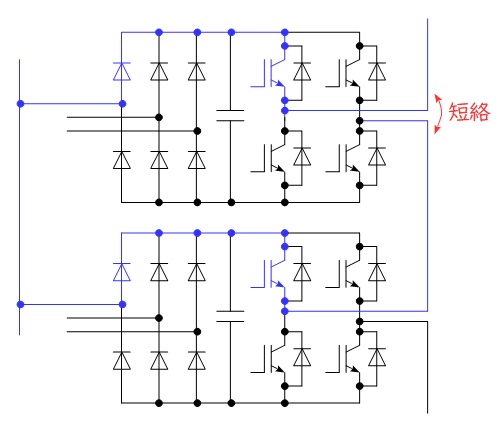
(3)解答:ニ
題意より解答候補は,(ニ)パルス幅,(リ)パルス振幅,(ワ)パルス周波数,になると思います。図2がヒントとなっていますが,パルス幅\( \ \theta \ \)で出力の交流電圧をコントロールします。
(4)解答:ヲ
問題文より,\( \ 5 \ \)次高調波を除去するためには,
\[
\begin{eqnarray}
\sin 5 \omega t +\sin 5\left( \omega t-\phi \right) &=&0 \\[ 5pt ]
\end{eqnarray}
\]
の関係があれば良いから,この式をワンポイント解説「1.三角関数の和積の公式」を使用して変形すると,
\[
\begin{eqnarray}
\sin 5 \omega t +\sin 5\left( \omega t-\phi \right) &=&0 \\[ 5pt ]
2\sin \frac {5 \omega t +5\left( \omega t-\phi \right) }{2} \cos \frac {5 \omega t -5\left( \omega t-\phi \right) }{2} &=&0 \\[ 5pt ]
2\sin \frac {10 \omega t -5\phi }{2} \cos \frac {5\phi }{2} &=&0 \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ t \ \)によらず等式が成り立つためには,
\[
\begin{eqnarray}
\cos \frac {5\phi }{2} &=&0 \\[ 5pt ]
\frac {5\phi }{2} &=&\frac {\pi }{2} \\[ 5pt ]
\phi &=&\frac {\pi }{5} \\[ 5pt ]
\end{eqnarray}
\]
となり,同様に\( \ 7 \ \)次高調波を除去するためには,
\[
\begin{eqnarray}
\phi &=&\frac {\pi }{7} \\[ 5pt ]
\end{eqnarray}
\]
となるから,両方の高調波を除去するためには,\( \ \displaystyle \phi =\frac {\pi }{6} \ \)が望ましいことが分かる。
(5)解答:ル
\( \ n=2 \ \)としたときの基本波電圧の大きさは,
\[
\begin{eqnarray}
\sin \omega t +\sin \left( \omega t-\phi \right) \\[ 5pt ]
\end{eqnarray}
\]
であり,ワンポイント解説「1.三角関数の和積の公式」を使用して変形すると,
\[
\begin{eqnarray}
\sin \omega t +\sin \left( \omega t-\phi \right) &=&2\sin \frac {2 \omega t -\phi }{2} \cos \frac {\phi }{2} \\[ 5pt ]
&=&2\cos \frac {\phi }{2}\sin \frac {2 \omega t -\phi }{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,振幅は\( \ \displaystyle 2\cos \frac {\phi }{2} \ \)となるので、\( \ \phi ≠0 \ \)ならば基本波のユニットは\( \ 2 \ \)倍未満の電圧となる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは