《電力》〈送電〉[H22:問4]電力系統の有効電力と電圧の特性に関する空欄穴埋問題

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，電力系統の有効電力と電圧の特性に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切な語句又は数値を解答群の中から選びなさい。

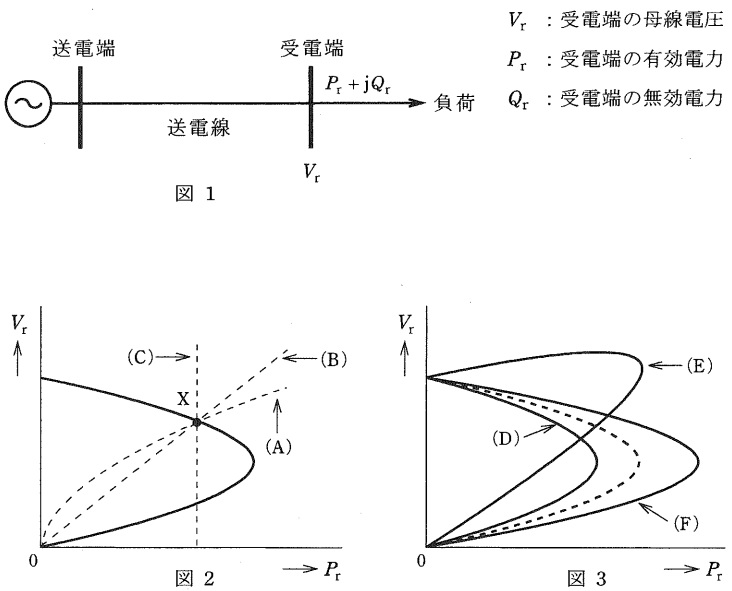
図2の実線は図1の受電端の母線における有効電力\( \ P_{\mathrm {r}} \ \)と母線電圧\( \ V_{\mathrm {r}} \ \)との関係を表した\( \ P – V \ \)曲線と呼ばれるものである。これに対して，図2の点線\( \ \left( \mathrm {A} \right) \ \)，\(\left( \mathrm {B} \right) \ \)及び\( \ \left( \mathrm {C} \right) \ \)は受電端母線から下位系につながる負荷の\( \ 3 \ \)種類の負荷特性を表しており，\( \ P – V \ \)曲線と負荷特性が交差する\( \ \mathrm {X} \ \)点がこの系統の\( \ \fbox {　 （１） 　} \ \)となる。一般に，負荷の電圧特性は次の式により表される。（受電端の基準電圧\( \ V_{\mathrm {0}} \ \)のときの負荷の有効電力，無効電力をそれぞれ\( \ P_{\mathrm {0}} \ \)，\( \ Q_{\mathrm {0}} \ \)とする。）
\[
\begin{eqnarray}
P_{\mathrm {r}}&=&P_{\mathrm {0}}\left( \frac {V_{\mathrm {r}}}{V_{\mathrm {0}}}\right) ^{\alpha },　Q_{\mathrm {r}}&=&Q_{\mathrm {0}}\left( \frac {V_{\mathrm {r}}}{V_{\mathrm {0}}}\right) ^{\beta } \\[ 5pt ] \end{eqnarray}
\] ここで，\( \ \alpha =\beta = \ \fbox {　 （２） 　} \ \)のとき，この負荷の持つ電圧特性は定電力特性と呼ばれ，その特性は図2中の\( \ \fbox {　 （３） 　} \ \)で表される。図2において定電力特性の負荷が増加すると，\( \ \fbox {　 （３） 　} \ \)は\( \ \fbox {　 （４） 　} \ \)するため，負荷の増加が大きいと\( \ P – V \ \)曲線と交差しなくなり，電圧不安定要因の一つとなる。

また，図3の点線を力率が\( \ 1 \ \)の場合の\( \ P – V \ \)曲線とし，負荷力率を変化させていった場合，実線\( \ \left( \mathrm {D} \right) \ \)，\(\left( \mathrm {E} \right) \ \)及び\( \ \left( \mathrm {F} \right) \ \)のうち負荷力率が遅れであるものは\( \ \fbox {　 （５） 　} \ \)である。

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　点線 \ \left( \mathrm {B} \right)　　　　　&（ロ）&　1　　　　　&（ハ）&　2 \\[ 5pt ] &（ニ）&　点線 \ \left( \mathrm {C} \right)　　　　　&（ホ）&　傾きが増加　　　　　&（ヘ）&　傾きが減少 \\[ 5pt ] &（ト）&　右側へ移動　　　　　&（チ）&　電圧安定限界点　　　　　　　&（リ）&　送電限界点 \\[ 5pt ] &（ヌ）&　運転点　　　　&（ル）&　実線 \ \left( \mathrm {D} \right)　　　　　&（ヲ）&　点線 \ \left( \mathrm {A} \right) \\[ 5pt ] &（ワ）&　0　　　　　&（カ）&　実線 \ \left( \mathrm {F} \right)　　　　&（ヨ）&　実線 \ \left( \mathrm {E} \right) \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

電力系統の有効電力と電圧の特性に関する問題です。
問題図2や図3の特性はノーズカーブとも呼ばれ，電圧の安定性を図る指標として用いられます。
ワンポイント解説で示している導出はかなりの計算量を必要とするため，電験対策としては一旦は図を見ながら暗記するような形が良いかと思います。

1.受電端母線の電圧の大きさ\( \ V_{\mathrm {r}} \ \)と受電端有効電力\( \ P \ \)の間の関係（\( \ P-V \ \)カーブ）
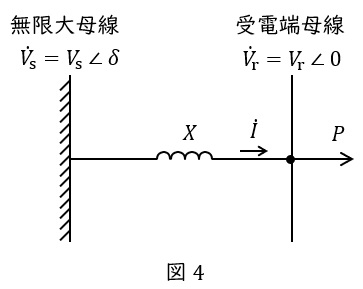
図4のような無限大母線（電圧\( \ {\dot V}_{\mathrm {s}}=V_{\mathrm {s}}∠\delta \ \)）からリアクタンス\( \ X \ \)及び受電側母線（電圧\( \ {\dot V}_{\mathrm {r}}=V_{\mathrm {r}}∠0 \ \)）を介して抵抗負荷に電力\( \ P \ \)を供給している系統を考えます。
（ここでは，簡単のため抵抗負荷を使用していますが，ノーズカーブの形は抵抗負荷以外でも同じとなります。さらに詳しく知りたい方は専門書を探して見て下さい。）
リアクタンスを流れる電流を\( \ \dot I \ \)とすると，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {s}}-{\dot V}_{\mathrm {r}}&=&\mathrm {j}X\dot I \\[ 5pt ] \dot I&=&\frac {V_{\mathrm {s}}∠\delta -V_{\mathrm {r}}}{\mathrm {j}X} \\[ 5pt ] \end{eqnarray}
\] となり，受電端複素電力\( \ P \ \)は，
\[
\begin{eqnarray}
P&=&{\dot V}_{\mathrm {r}}\overline {\dot I} \\[ 5pt ] &=&V_{\mathrm {r}}\cdot \frac {V_{\mathrm {s}}∠\left( -\delta \right) -V_{\mathrm {r}}}{-\mathrm {j}X} \\[ 5pt ] &=&\mathrm {j}V_{\mathrm {r}}\cdot \frac {V_{\mathrm {s}}∠\left( -\delta \right) -V_{\mathrm {r}}}{X} \\[ 5pt ] &=&\frac {V_{\mathrm {s}}V_{\mathrm {r}}∠\left( -\delta +\displaystyle \frac {\pi }{2}\right) -\mathrm {j}V_{\mathrm {r}}^{2}}{X} \\[ 5pt ] P+\mathrm {j}\frac {V_{\mathrm {r}}^{2}}{X}&=&\frac {V_{\mathrm {s}}V_{\mathrm {r}}∠\left( -\delta +\displaystyle \frac {\pi }{2}\right) }{X} \\[ 5pt ] \end{eqnarray}
\] となります。両辺の大きさ（絶対値）は等しいので，
\[
\begin{eqnarray}
P^{2}+\left( \frac {V_{\mathrm {r}}^{2}}{X}\right) ^{2}&=&\left( \frac {V_{\mathrm {s}}V_{\mathrm {r}}}{X}\right) ^{2} \\[ 5pt ] \end{eqnarray}
\] となり，これを\( \ V_{\mathrm {r}} \ \)について整理して\( \ V_{\mathrm {r}} \ \)を求めると，
\[
\begin{eqnarray}
\frac {V_{\mathrm {r}}^{4}}{X^{2}}-\frac {V_{\mathrm {s}}^{2}V_{\mathrm {r}}^{2}}{X^{2}}+P^{2}&=&0 \\[ 5pt ] V_{\mathrm {r}}^{4}-V_{\mathrm {s}}^{2}V_{\mathrm {r}}^{2}+X^{2}P^{2}&=&0 \\[ 5pt ] V_{\mathrm {r}}^{2}&=&\frac {V_{\mathrm {s}}^{2}±\sqrt {V_{\mathrm {s}}^{4}-4X^{2}P^{2}}}{2} \\[ 5pt ] V_{\mathrm {r}}&=&\sqrt {\frac {V_{\mathrm {s}}^{2}±\sqrt {V_{\mathrm {s}}^{4}-4X^{2}P^{2}}}{2}} \\[ 5pt ] \end{eqnarray}
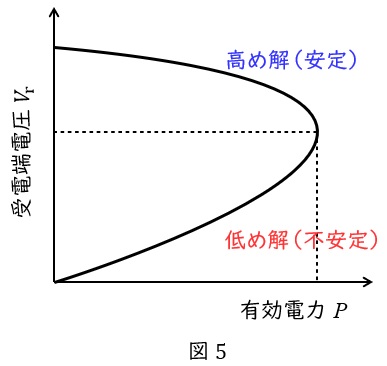
\] と求められます。上式について，受電端母線の電圧\( \ V_{\mathrm {r}} \ \)と受電端電力\( \ P \ \)の間の関係（\( \ P-V \ \)カーブ）を描くと図5のようになり，これをノーズカーブと呼びます。
図5より，同じ電力において電圧が\( \ 2 \ \)点ある（上式の\( \ 2 \ \)つの解）ことが分かり，電圧が高い方を高め解（安定），電圧が低い方を低め解（不安定）と言います。

2.\( \ P-V \ \)カーブにおける定電力，定電流，定インピーダンス特性
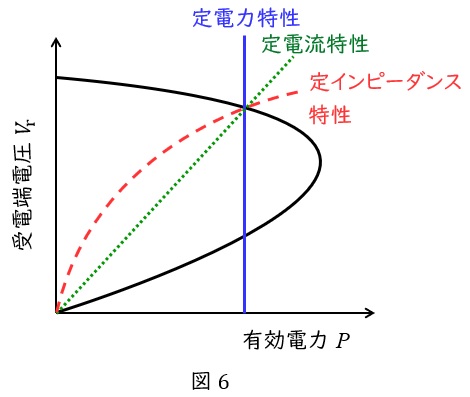
定電力特性はその名の通り\( \ P \ \)一定の特性なので，図6の青線のような特性となり，定電流特性は\( \ \displaystyle V∝\frac {P}{I} \ \)の関係より図6の緑線のような特性，定インピーダンス特性は，\( \ \displaystyle P∝\frac {V^{2}}{Z} \ \)すなわち\( \ V∝\sqrt {ZP} \ \)の関係があるので，図6の赤線のような特性となります。

【関連する「電気の神髄」記事】

　　電力系統のP-V曲線と電圧安定性

【解答】

(1)解答：ヌ
題意より解答候補は，（チ）電圧安定限界点，（リ）送電限界点，（ヌ）運転点，になると思います。
\( \ P – V \ \)曲線と負荷特性が交差する\( \ \mathrm {X} \ \)点を運転点と呼びます。

(2)解答：ワ
題意より解答候補は，（ロ）\( \ 1 \ \)，（ハ）\( \ 2 \ \)，（ワ）\( \ 0 \ \)，になると思います。
定電力特性は電力が一定の特性なので，\( \ \alpha =\beta = 0 \ \)でないと成立しません。

(3)解答：ニ
題意より解答候補は，（イ）点線\( \ \left( \mathrm {B} \right) \ \)，（ニ）点線\( \ \left( \mathrm {C} \right) \ \)，（ヲ）点線\( \ \left( \mathrm {A} \right) \ \)，になると思います。
ワンポイント解説「2.\( \ P-V \ \)カーブにおける定電力，定電流，定インピーダンス特性」の通り，定電力特性を表しているのは点線\( \ \left( \mathrm {C} \right) \ \)となります。

(4)解答：ト
題意より解答候補は，（ホ）傾きが増加，（ヘ）傾きが減少，（ト）右側へ移動，になると思います。
定電力特性において，グラフの特性は変化しないため，負荷が増加すると右側へ移動し，\( \ P – V \ \)曲線と交差しなくなり電圧不安定となります。

(5)解答：ル
題意より解答候補は，（ル）実線\( \ \left( \mathrm {D} \right) \ \)，（カ）実線\( \ \left( \mathrm {F} \right) \ \)，（ヨ）実線\( \ \left( \mathrm {E} \right) \ \)，になると思います。
負荷力率が遅れになると送電線での電圧降下が大きくなることでノーズカーブは小さくなり，実線\( \ \left( \mathrm {D} \right) \ \)のようなカーブを描きます。