《機械》〈照明〉[H19:問6]照明分野における測光量と単位に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★☆☆☆☆（易しい）

次の文章は，測光量と単位に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる語句，式又は数値を解答群の中から選び，その記号をマークシートに記入しなさい。

照明の基本的な単位である$ \ \fbox {　（１）　} \ $は，波長域$ \ 380 \ \mathrm {[nm]} \sim 780 \ \mathrm {[nm]} \ $の光放射に，人間の目の明るさ感覚を代表する「標準比視感度」を乗じたものであり，波長$ \ \fbox {　（２）　} \ \mathrm {[nm]} \ $の$ \ 1 \ \mathrm {[W]} \ $の光放射が$ \ 683 \ \mathrm {[lm]} \ $となるよう定義されている。光度は，ある方向への光の強度を表わす光の単位で，ある方向の光束の$ \ \fbox {　（３）　} \ $で表される。光度の単位は$ \ \mathrm {[cd]} \ $である。照度は，$ \ \fbox {　（４）　} \ $に入射する光束で，単位は$ \ \mathrm {[lx]} \ $である。輝度は，光源や照らされた面の輝きを表し，人の明るさ感覚と密接に関係する。輝度の単位は$ \ [ \ \fbox {　（５）　} \ ] \ $である.

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　\mathrm {lm/m^{2}}　　　　　　　&（ロ）&　1 \ \mathrm {[m^{2}]} \ 当たり　　　　　&（ハ）&　531 \\[ 5pt ] &（ニ）&　放射束　　　　　&（ホ）&　面積密度　　　　　&（ヘ）&　光　束 \\[ 5pt ] &（ト）&　\mathrm {cd/m^{2}}　　　　　&（チ）&　体積密度　　　　　　　&（リ）&　555 \\[ 5pt ] &（ヌ）&　1 \ \mathrm {[{cm}^{2}]} \ 当たり　　　　　&（ル）&　立体角密度　　　　　&（ヲ）&　507 \\[ 5pt ] &（ワ）&　\mathrm {rix/m^{2}}　　　　　&（カ）&　光束発散度　　　　　&（ヨ）&　1 \ \mathrm {[{mm}^{2}]} \ 当たり \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

照明分野における測光量と単位に関する問題です。
本問に出題されている内容はいずれも照明の基本となる重要な内容です。全問正答できるように準備しておきましょう。

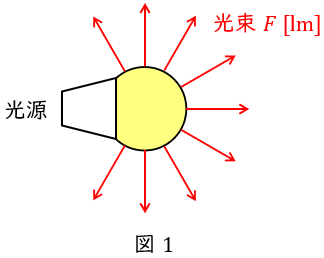
1.光束$ \ F \ $
光源から出る可視光の量（エネルギー）で，単位は$ \ \mathrm {[lm]} \ $となります。
電磁気の分野の電束に似たようなイメージで良いです。

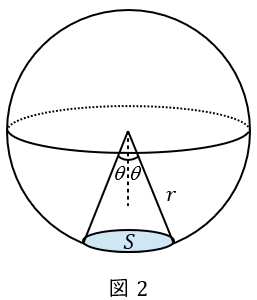
2.立体角の定義
図2のように球体があり，半径$ \ r \ \mathrm {[m]} \ $の錐体が球面を切り取った時の面積を$ \ S \ \mathrm {[m^{2}]} \ $とすると，立体角$ \ \omega \ \mathrm {[sr]} \ $は，
\[
\begin{eqnarray}
\omega &=&\frac {S}{r^{2}} \\[ 5pt ] \end{eqnarray}
\] であり，平面角$ \ \theta \ \mathrm {[rad]} \ $で表すと，
\[
\begin{eqnarray}
\omega &=&2\pi \left( 1-\cos \theta \right) \\[ 5pt ] \end{eqnarray}
\] となります。球全体の立体角は$ \ \theta = \pi \ $の時であり，$ \ \omega =4\pi \ $となります。

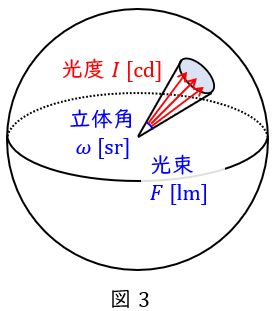
3.光度$ \ I \ $
ある方向に向かう光束$ \ F \ \mathrm {[lm]} \ $を立体角$ \ \omega \ \mathrm {[sr]} \ $で割ったもので，光度$ \ I \ \mathrm {[cd]} \ $を式で表すと，
\[
\begin{eqnarray}
I &=&\frac {F}{\omega } \\[ 5pt ] \end{eqnarray}
\] となります。

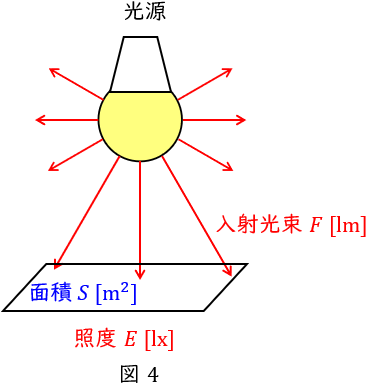
4.照度$ \ E \ $
図4のように，光源からある方向へ向かう光度が$ \ I \ \mathrm {[cd]} \ $であるとき，光源からの距離$ \ l \ \mathrm {[m]} \ $離れた垂直面の照度$ \ E \ \mathrm {[lx]} \ $は，
\[
\begin{eqnarray}
E&=&\frac {I}{l^{2}} \\[ 5pt ] \end{eqnarray}
\] で求められます。このように，一般に物理量が$ \ 2 \ $乗に反比例する法則を逆$ \ 2 \ $乗の法則といいます。

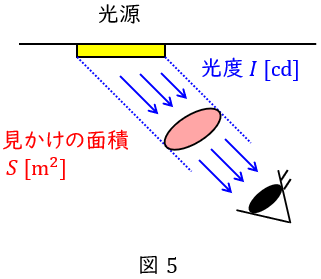
5.輝度$ \ L \ $
図5のように，ある方向から見た光源のまぶしさを表す指標で，光源からある方向へ向かう光度が$ \ I \ \mathrm {[cd]} \ $であるとき，輝度$ \ L \ \mathrm {[cd/m^{2}]} \ $は，同じ方向から照明を見た投影面積を$ \ S \ \mathrm {[m^{2}]} \ $とすると，
\[
\begin{eqnarray}
L&=&\frac {I}{S} \\[ 5pt ] \end{eqnarray}
\] で求められます。

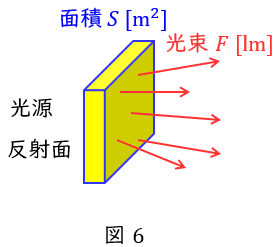
6.光束発散度$ \ M \ $
光源・反射面・透過面等の単位面積あたりから発散する光束をいい，面積$ \ S \ \mathrm {[m^{2}]} \ $から発散する光束を$ \ F \ \mathrm {[lm]} \ $とすると，光束発散度$ \ M \ \mathrm {[lm/m^{2}]} \ $は，
\[
\begin{eqnarray}
M&=&\frac {F}{S} \\[ 5pt ] \end{eqnarray}
\] となります。

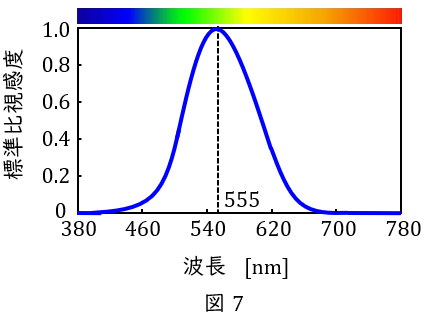
7.標準比視感度
人間の光に対する感度を表したものです。図7のように約$ \ 555 \ \mathrm {nm} \ $を最大値として，波長によって異なる心理物理量の割合を示しています。

【解答】

(1)解答：ヘ
題意より，解答候補は（ニ）放射束，（ヘ）光束，（カ）光束発散度，になると思います。
ワンポイント解説「1.光束$ \ F \ $」の通り，照明の基本的な単位は光束となります。光束$ \ F \ \mathrm {[lm]} \ $は波長を$ \ \lambda \ \mathrm {[nm]} \ $，分光放射束を$ \ P\left( \lambda \right) \ \mathrm {[W / nm]} \ $，標準比視感度を$ \ V\left( \lambda \right) \ $，$ \ V\left( \lambda \right) \ $が最大となる波長における放射束と光束の換算係数$ \ K_{\mathrm {m}} \ $$\left( =683 \ \mathrm {lm / W} \right) \ $とすると，
\[
\begin{eqnarray}
F &=& K_{\mathrm {m}}\int _{380} ^{780}V\left( \lambda \right) P\left( \lambda \right) \mathrm {d}\lambda \\[ 5pt ] \end{eqnarray}
\] で求められます。

(2)解答：リ
題意より，解答候補は（ハ）$ \ 531 \ $，（リ）$ \ 555 \ $，（ヲ）$ \ 507 \ $，になると思います。
ワンポイント解説「7.標準比視感度」の通り，波長$ \ 555 \ \mathrm {[nm]} \ $の$ \ 1 \ \mathrm {[W]} \ $の光放射が$ \ 683 \ \mathrm {[lm]} \ $となるよう定義されています。

(3)解答：ル
題意より，解答候補は（ホ）面積密度，（チ）体積密度，（ル）立体角密度，になると思います。
ワンポイント解説「3.光度$ \ I \ $」の通り，光度は，ある方向への光の強度を表わす光の単位で，ある方向の光束の立体角密度で表されます。

(4)解答：ロ
題意より，解答候補は（ロ）$ \ 1 \ \mathrm {[m^{2}]} \ $当たり，（ヌ）$ \ 1 \ \mathrm {[{cm}^{2}]} \ $当たり，（ヨ）$ \ 1 \ \mathrm {[{mm}^{2}]} \ $当たり，になると思います。
ワンポイント解説「4.照度$ \ E \ $」の通り，$ \ 1 \ \mathrm {[m^{2}]} \ $当たりに入射する光束で，単位は$ \ \mathrm {[lx]} \ $となります。

(5)解答：ト
題意より，解答候補は（イ）$ \ \mathrm {lm/m^{2}} \ $，（ト）$ \ \mathrm {cd/m^{2}} \ $，（ワ）$ \ \mathrm {rix/m^{2}} \ $，になると思います。
ワンポイント解説「5.輝度$ \ L \ $」の通り，輝度の単位は$ \ \mathrm {[cd/m^{2}]} \ $となります。