《機械》〈電熱〉[H19:問7]電気加熱のうち誘電加熱に関する空欄穴埋問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，誘電加熱に関する記述である 文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる語句を解答群の中から選び，その記号をマークシートに記入しなさい。

誘電体を高周波電界中に配置し，主として誘電体自身の電気\( \ \fbox {　 （１） 　} \ \)作用による損失で発熱・昇温させる加熱方式を誘電加熱と呼ぶ。誘電加熱の中で周波数帯が\( \ 300 \ \mathrm {[MHz]} \sim 30 \ \mathrm {[GHz]} \ \)範囲を使用するものを，特に\( \ \fbox {　 （２） 　} \ \)加熱と称し区別している。

誘電加熱で発熱に要する単位体積当たりの電力は，印加する電界の強さ\( \ E \ \mathrm {[V/m]} \ \)の\( \ \fbox {　 （３） 　} \ \)及び印加する周波数\( \ f \ \mathrm {[Hz]} \ \)，被加熱物の比誘電率\( \ \varepsilon _{r} \ \)，誘電正接\( \ \tan \delta \ \)に比例する。\( \ \varepsilon _{r} \cdot \tan \delta \ \)を誘電損失係数と呼び，誘電加熱の容易さを判断する目安となる。この値が\( \ 0.01 \ \)程度以下の物質については誘電加熱が困難である。

なお，実際の適用では，通信設備への電波妨害や生体への影響等の考慮が必要で，周波数は電波法で\( \ \fbox {　 （４） 　} \ \)周波数として，使用できる数値が決められている。

誘電損失係数の差を利用して，例えば木材の接着には接着部分のみの加熱や，包装材が誘電率の小さいものであれば，内部の食品のみの加熱など，加熱部分の選択を行うことができる。

外部からの加熱による昇温のように，被加熱物自体の\( \ \fbox {　 （５） 　} \ \)に依存せず被加熱物を内部から加熱するので，急速で均一な加熱を行うことが可能である。

〔問7の解答群〕
\[
\begin{eqnarray}
&（イ）&　分　極　　　　　&（ロ）&　誘　導　　　　　&（ハ）&　\mathrm {EMC} \\[ 5pt ] &（ニ）&　2　乗　　　　　&（ホ）&　熱放射　　　　　&（ヘ）&　3　乗 \\[ 5pt ] &（ト）&　分　解　　　　　&（チ）&　マイクロ波　　　　　　　&（リ）&　1 / 2 \ 乗 \\[ 5pt ] &（ヌ）&　\mathrm {ISM}　　　　　&（ル）&　熱対流　　　　　&（ヲ）&　\mathrm {EMI} \\[ 5pt ] &（ワ）&　熱伝導　　　　　　　&（カ）&　磁　力　　　　　&（ヨ）&　高調波 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

誘電加熱の原理と特徴に関する問題です。
(3)以降の空欄が少しマイナーな内容なので，誘電加熱の問題としては少し難易度が高い問題と言えるかと思います。

1.誘電加熱
交番電界中に誘電体を置くことによって，誘電体に誘電損が生じ発熱することを利用した加熱方式です。
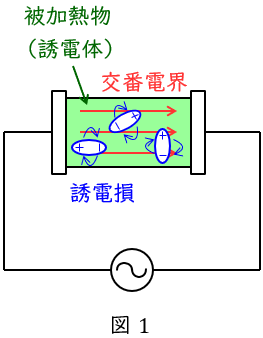
図1のように平行板電極に被加熱物（誘電体）を挿入し，高周波の電界を加えることで，誘電分極した電気双極子が振動・回転することにより発熱します。
誘電加熱のうち周波数帯が\( \ 300 \ \mathrm {[MHz]} \sim 30 \ \mathrm {[GHz]} \ \)範囲を使用するものをマイクロ波加熱といい，電子レンジはこの原理を利用した電化製品の一つです。

2.誘電損\( \ W_{\mathrm {d}} \ \mathrm {[W]} \ \)
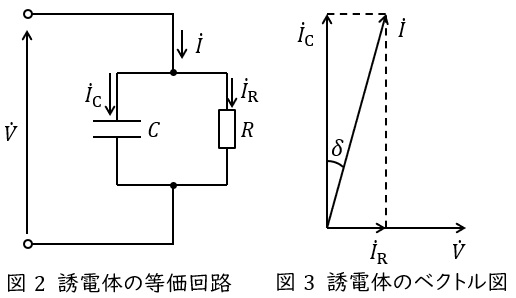
誘電体の等価回路は図2のように抵抗\( \ R \ \mathrm {[\Omega ]} \ \)と静電容量\( \ C \ \mathrm {[F]} \ \)の並列回路となり，コンデンサには図3のようなベクトル図の電流が流れます。この時の\( \ \displaystyle \frac {I_{\mathrm {R}}}{I_{\mathrm {C}}}=\tan \delta \ \)を誘電正接と呼びます。この等価回路における発熱にかかる誘電損\( \ W_{\mathrm {d}} \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
W_{\mathrm {d}}&=&VI_{\mathrm {R}} \\[ 5pt ] &=&VI_{\mathrm {C}}\tan \delta \\[ 5pt ] &=&V\omega CV\tan \delta \\[ 5pt ] &=&\omega CV^{2}\tan \delta \\[ 5pt ] &=&2\pi f \frac {\varepsilon _{\mathrm {r}}\varepsilon _{\mathrm {0}}S}{d}E^{2}d^{2}\tan \delta \\[ 5pt ] &=&2\pi fSdE^{2} \varepsilon _{\mathrm {0}}\varepsilon _{\mathrm {r}}\tan \delta \\[ 5pt ] \end{eqnarray}
\] となり，発熱量は，電界\( \ E \ \mathrm {[V / m]} \ \)の\( \ 2 \ \)乗に比例し，周波数\( \ f \ \mathrm {[Hz]} \ \)，比誘電率\( \ \varepsilon _{\mathrm {r}} \ \)，誘電正接\( \ \tan \delta \ \)に比例することがわかります。\( \ \varepsilon _{\mathrm {r}}\tan \delta \ \)を損失係数といいます。

【解答】

(1)解答：イ
題意より，解答候補は（イ）分極，（ロ）誘導，（ト）分解，（カ）磁力，になると思います。
ワンポイント解説「1.誘電加熱」の通り，誘電加熱は誘電体を高周波電界中に配置し，誘電体自身の電気分極作用による損失で発熱・昇温させる加熱方式です。

(2)解答：チ
題意より，解答候補は（ロ）誘導，（チ）マイクロ波，（ヨ）高調波，等になると思います。
ワンポイント解説「1.誘電加熱」の通り，誘電加熱の中で周波数帯が\( \ 300 \ \mathrm {[MHz]} \sim 30 \ \mathrm {[GHz]} \ \)範囲を使用するものを，特にマイクロ波加熱といいます。

(3)解答：ニ
題意より，解答候補は（ニ）\( \ 2 \ \)乗，（ヘ）\( \ 3 \ \)乗，（リ）\( \ 1 / 2 \ \)乗，になると思います。
ワンポイント解説「2.誘電損\( \ W_{\mathrm {d}} \ \mathrm {[W]} \ \)」の通り，誘電加熱で発熱に要する単位体積当たりの電力は，印加する電界の強さ\( \ E \ \mathrm {[V/m]} \ \)の\( \ 2 \ \)乗に比例します。

(4)解答：ヌ
題意より，解答候補は（ハ）\( \ \mathrm {EMC} \ \)，（ヌ）\( \ \mathrm {ISM} \ \)，（ヲ）\( \ \mathrm {EMI} \ \)，になると思います。
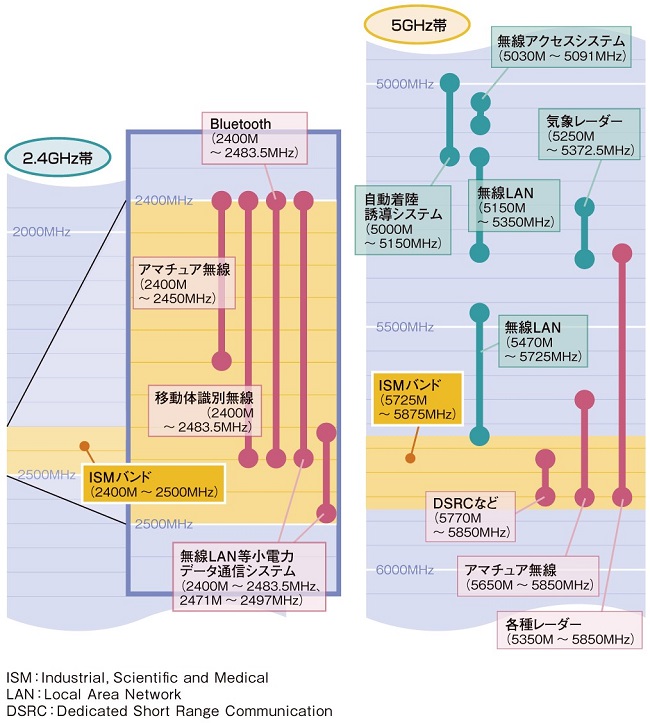
下図に示すように，電波法で放送などの無線業務の障害となるのを避けるために割り当てられた周波数の帯を\( \ \mathrm {ISM} \ \)周波数帯と言います。

出典：日経クロステック　ISMバンド　2010,09.22　記事

(5)解答：ワ
題意より，解答候補は（ホ）熱放射，（ル）熱対流，（ワ）熱伝導，等になると思います。
このうち被加熱物自体が加熱されるのは熱伝導となります。熱対流は水などの液体が移動することによる熱の移動，熱放射は熱源から電磁波としてエネルギーが放出されることによる熱が移動となります。