Contents
【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,三相誘導電動機に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
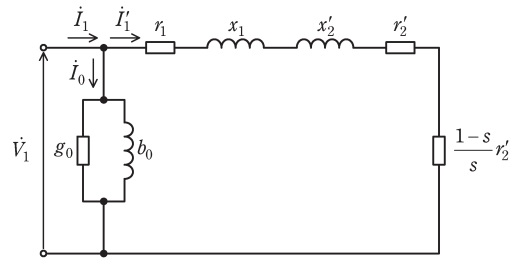
図は,三相誘導電動機の\( \ 1 \ \)相分の\( \ \mathrm {L} \ \)形等価回路である。ただし,\( \ r_{1} \ \)は一次巻線抵抗,\( \ r_{2}^{\prime } \ \)は二次巻線抵抗の一次換算値,\( \ x_{1} \ \)は一次漏れリアクタンス,\( \ x_{2}^{\prime } \ \)は二次漏れリアクタンスの一次換算値,\( \ b_{0} \ \)及び\( \ g_{0} \ \)は励磁サセプタンス及び励磁コンダクタンスである。三相交流電源の相電圧の実効値を\( \ V_{1} \ \),フェーザを\( \ {\dot V}_{1} \ \)とする。また,滑りを\( \ s \ \)とし,漏れリアクタンスの和を\( \ X=x_{1}+x_{2}^{\prime } \ \)とする。
電動機を交流電源に接続すると,励磁電流は\( \ {\dot I}_{0}=\fbox { (1) } \ \)となり,\( \ {\dot I}_{0} \ \)による損失は\( \ W_{\mathrm {I}}=\fbox { (2) } \ \)である。機械損\( \ W_{\mathrm {m}} \ \)を無視すると,機械的出力は\( \ P_{\mathrm {O}}=\fbox { (3) }\)である。一方,\( \ r_{1} \ \)及び\( \ r_{2}^{\prime } \ \)に生じる損失は\( \ W_{\mathrm {C}}=\fbox { (4) } \ \)となる。
ここで,機械損\( \ W_{\mathrm {m}} \ \)を考慮すると,電動機の効率は\( \ \fbox { (5) } \ \)となる。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {P_{\mathrm {O}}-W_{\mathrm {m}}}{P_{\mathrm {O}}+W_{\mathrm {I}}+W_{\mathrm {C}}} &(ロ)& \frac {\displaystyle 3\frac {1-s}{s}r_{2}^{\prime }V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime }}{s}\right) ^{2}+X^{2}} &(ハ)& 3\frac {V_{1}^{2}}{g_{0}} \\[ 5pt ]
&(ニ)& \frac {{\dot V}_{1}}{g_{0}-\mathrm {j}b_{0}} &(ホ)& \frac {\displaystyle 3\left( r_{1}+\frac {r_{2}^{\prime }}{s}\right) V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime }}{s}\right) ^{2}+X^{2}} &(ヘ)& 3\frac {V_{1}^{2}}{\sqrt {g_{0}^{2}+b_{0}^{2}}} \\[ 5pt ]
&(ト)& \frac {\displaystyle 3r_{1}V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime }}{s}\right) ^{2}+X^{2}} &(チ)& \frac {\displaystyle 3\left( r_{1}+r_{2}^{\prime }\right) V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime }}{s}\right) ^{2}+X^{2}} &(リ)& \left( g_{0}+\mathrm {j}b_{0}\right) {\dot V}_{1} \\[ 5pt ]
&(ヌ)& \frac {\displaystyle 3\frac {r_{2}^{\prime }}{s}V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime }}{s}\right) ^{2}+X^{2}} &(ル)& \left( g_{0}-\mathrm {j}b_{0}\right) {\dot V}_{1} &(ヲ)& 3g_{0}V_{1}^{2} \\[ 5pt ]
&(ワ)& \frac {\displaystyle 3r_{2}^{\prime }V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime }}{s}\right) ^{2}+X^{2}} &(カ)& \frac {P_{\mathrm {O}}-W_{\mathrm {C}}-W_{\mathrm {m}}}{P_{\mathrm {O}}+W_{\mathrm {I}}} &(ヨ)& \frac {P_{\mathrm {O}}}{P_{\mathrm {O}}+W_{\mathrm {I}}+W_{\mathrm {C}}+W_{\mathrm {m}}} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
誘導電動機の問題としては非常に出題されやすい重要問題と言えると思います。計算力の必要な問題なのでやや難しいとしていますが,等価回路を描いて,二次入力と出力を導出する計算方法は完全にパターン化されています。限られた時間の中でできるだけ早く計算できる様準備するようにして下さい。
1.誘導電動機の\( \ \mathrm {L} \ \)形等価回路
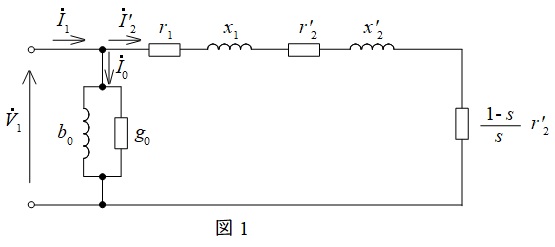
本問では\( \ \mathrm {L} \ \)形等価回路が記載されていますが,基本的には\( \ \mathrm {L} \ \)形等価回路は描けるようにしておいた方が良いと思います。ちなみに問題では\( \ I_{1}^{\prime } \ \)を使用していますが,一般的には\( \ I_{2}^{\prime } \ \)を使用します。問題の内容以外にも図1下の計算はできるようにしておきましょう。
\[
\begin{eqnarray}
V_{1}&:&一次電圧 \\[ 5pt ]
I_{1}&:&一次電流 \\[ 5pt ]
I_{0}&:&励磁電流 \\[ 5pt ]
I^{\prime}_{2}&:&一次側に換算した二次電流 \\[ 5pt ]
r_{1}&:&一次抵抗 \\[ 5pt ]
x_{1}&:&一次リアクタンス \\[ 5pt ]
r_{2}^{\prime}&:&一次側に換算した二次抵抗 \\[ 5pt ]
x_{2}^{\prime}&:&一次側に換算した二次リアクタンス \\[ 5pt ]
g_{0}&:&励磁コンダクタンス \\[ 5pt ]
b_{0}&:&励磁サセプタンス \\[ 5pt ]
s&:&滑り
\end{eqnarray}
\]
図1より,
\[
\begin{eqnarray}
I_{2}^{\prime } &=& \frac {V_{1}}{\displaystyle \sqrt{\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となるから,二次入力\( \ P_{2} \ \)は,
\[
\begin{eqnarray}
P_{2}&=&3\frac {r_{2}^{\prime}}{s}{I^{\prime}_{2}}^{2} \\[ 5pt ]
&=&3\frac {r_{2}^{\prime}}{s}\cdot \left( {\frac {V_{1}}{\displaystyle \sqrt{\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}}}\right) ^{2} \\[ 5pt ]
&=&\frac {3r_{2}^{\prime}}{s}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}
\end{eqnarray}
\]
となり,発生するトルク\( \ T \ \)は,
\[
\begin{eqnarray}
T&=&\frac {P_{o}}{\omega } \\[ 5pt ]
&=&\frac {(1-s)P_{2}}{(1-s)\omega _{s}} \\[ 5pt ]
&=&\frac {P_{2}}{\omega _{s}} \\[ 5pt ]
&=&\frac {3r_{2}^{\prime}}{\omega _{s}s}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:ル
励磁回路にかかる電圧は\( \ {\dot V}_{1} \ \),励磁回路のアドミタンス\( \ {\dot Y}_{0} \ \)は\( \ {\dot Y}_{0}=\mathrm {g}_{0}-\mathrm {j}b_{0} \ \)であるため,励磁電流\( \ {\dot I}_{0} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{0}&=&{\dot Y}_{0}{\dot V}_{1} \\[ 5pt ]
&=&\left( \mathrm {g}_{0}-\mathrm {j}b_{0}\right) {\dot V}_{1} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
※注意 \( \ b_{0} \ \)はコイルなので,アドミタンスとしては負の値となります。
(2)解答:ヲ
励磁回路による損失の大きさ\( \ W_{\mathrm {I}} \ \)は,\( \ \mathrm {g}_{0} \ \)にかかる電圧が\( \ {\dot V}_{1} \ \)であるから,
\[
\begin{eqnarray}
W_{\mathrm {I}}&=&3\mathrm {g}_{0}V_{1}^{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ロ
問題図より,
\[
\begin{eqnarray}
I_{1}^{\prime } &=& \frac {V_{1}}{\displaystyle \sqrt{\left( r_{1}+r_{2}^{\prime}+\frac {1-s}{s}r_{2}^{\prime}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}} \\[ 5pt ]
&=& \frac {V_{1}}{\displaystyle \sqrt{\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +X ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となるから,機械的出力\( \ P_{\mathrm {O}} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {O}}&=&3\frac {1-s}{s}r_{2}^{\prime}{I^{\prime}_{1}}^{2} \\[ 5pt ]
&=&3\frac {1-s}{s}r_{2}^{\prime}\cdot \left( {\frac {V_{1}}{\displaystyle \sqrt{\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +X ^{2}}}}\right) ^{2} \\[ 5pt ]
&=&3\frac {1-s}{s}r_{2}^{\prime}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +X ^{2}} \\[ 5pt ]
&=&\frac {\displaystyle 3\frac {1-s}{s}r_{2}^{\prime}V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +X ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:チ
(3)において\( \ I_{1}^{\prime } \ \)は導出されているので,\( \ r_{1} \ \)及び\( \ r_{2}^{\prime } \ \)に生じる損失\( \ W_{\mathrm {C}} \ \)は,
\[
\begin{eqnarray}
W_{\mathrm {C}}&=&3\left( r_{1}+r_{2}^{\prime}\right) {I^{\prime}_{1}}^{2} \\[ 5pt ]
&=&3\left( r_{1}+r_{2}^{\prime}\right) \cdot \left( {\frac {V_{1}}{\displaystyle \sqrt{\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +X ^{2}}}}\right) ^{2} \\[ 5pt ]
&=&3\left( r_{1}+r_{2}^{\prime}\right) \cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +X ^{2}} \\[ 5pt ]
&=&\frac {3\left( r_{1}+r_{2}^{\prime}\right) V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +X ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:イ
機械損\( \ W_{\mathrm {m}} \ \)を無視すると,電動機の効率\(\eta \)は,
\[
\begin{eqnarray}
\eta &=&\frac {出力}{入力} \\[ 5pt ]
&=&\frac {出力}{出力+損失} \\[ 5pt ]
&=&\frac {P_{\mathrm {O}}}{P_{\mathrm {O}}+W_{\mathrm {I}}+W_{\mathrm {C}}} \\[ 5pt ]
\end{eqnarray}
\]
となるが,機械損\( \ W_{\mathrm {m}} \ \)を考慮すると出力が減少するため,
\[
\begin{eqnarray}
\eta &=&\frac {P_{\mathrm {O}}-W_{\mathrm {m}}}{P_{\mathrm {O}}+W_{\mathrm {I}}+W_{\mathrm {C}}} \\[ 5pt ]
\end{eqnarray}
\]
となる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは