《機械》〈照明〉[R02:問6]ランベルトの余弦法則，光度と輝度の関係に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，ランベルトの余弦法則，光度と輝度との関係に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

面積$ \ \mathrm {d}S \ $，反射率$ \ \rho \ $の微小平面板があり，その片面だけが照度$ \ E \ $で照らされ，輝度$ \ L \ $で輝いている。この輝いている面の法線方向の光度を$ \ \mathrm {d}I_{\mathrm {n}} \ $とすれば，面の輝きを表す輝度$ \ L \ $は$ \ \fbox {　（１）　} \ $で与えられる。単位は$ \ \fbox {　（２）　} \ $である。

いま，この面を法線より斜め$ \ \theta \ $方向から見た輝度$ \ L_{\mathrm {\theta }} \ $は，投影面積$ \ \mathrm {d}S_{\mathrm {\theta }} \ $が$ \ \mathrm {d}S_{\mathrm {\theta }}= \ \fbox {　（３）　} \ $となり，その方向の光度を$ \ \mathrm {d}I_{\mathrm {\theta }} \ $とすれば$ \ \fbox {　（１）　} \ $と同様にして求まる。もし，$ \ L=L_{\mathrm {\theta }} \ $であれば，この面の鉛直配光は，$ \ \mathrm {d}I_{\mathrm {\theta }}=\mathrm {d}I_{\mathrm {n}}\cdot \cos \theta \ $となる関係が成立するので，$ \ \mathrm {d}I_{\mathrm {n}} \ $を直径とする円形となる。これをランベルトの余弦法則という。

どの方向から見ても輝度の等しい面を$ \ \fbox {　（４）　} \ $といい，ランベルトの余弦法則に従う面である。また，この面では，照度$ \ E \ $と輝度$ \ L \ $との間に$ \ \fbox {　（５）　} \ $なる関係がある。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　\mathrm {d}S\cdot \cos \theta 　　　　　&（ロ）&　\mathrm {d}S\cdot \sin \theta 　　　　　&（ハ）&　均等拡散面 \\[ 5pt ] &（ニ）&　L=\frac {\rho I_{\mathrm {n}}}{\mathrm {d}S}　　　　　&（ホ）&　\mathrm {d}S\cdot \tan \theta 　　　　　&（ヘ）&　L=\frac {\rho E}{\mathrm {d}S} \\[ 5pt ] &（ト）&　L=\frac {\mathrm {d} I_{\mathrm {n}}}{\mathrm {d}S}　　　　　&（チ）&　ラドルクス \ \left[ \mathrm {rlx} \right]　　　　　&（リ）&　完全反射面 \\[ 5pt ] &（ヌ）&　\pi E=\rho L　　　　　&（ル）&　\rho E=\pi L　　　　　&（ヲ）&　均等反射面 \\[ 5pt ] &（ワ）&　トロランド \ \left[ \mathrm {td} \right]　　　　　&（カ）&　\rho \pi E=L　　　　　&（ヨ）&　カンデラ毎平方メートル \ \left[ \mathrm {cd/m^{2}} \right] \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

ランベルトの余弦法則，光度や輝度等$ \ 3 \ $種の頃からよく見る問題であると思います。
しかしながら，計算問題が主であった$ \ 3 \ $種と異なり，$ \ 2 \ $種は計算問題がほぼなく，本問のように知識を問う問題が出題されます。
$ \ 2 \ $種対策のため，もう一度違った視点で復習するようにして下さい。

1.光束$ \ F \ $
光の量で単位はルーメン$ \ [ \mathrm {lm} ] \ $となります。電磁気で言うと磁束のようなものです。

2.照度$ \ E \ $
均一に照射された面の明るさで，面積$ \ A \ $に入射する光束を$ \ F \ $とすると，
\[
\begin{eqnarray}
E&=&\frac {F}{A} \ [ \mathrm {lx}] \\[ 5pt ] \end{eqnarray}
\] となります。

3.輝度$ \ L \ $
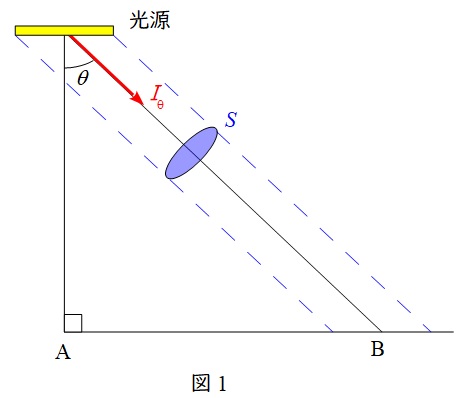
図1に示すように，$ \ \mathrm {B} \ $点から見た輝度は$ \ \mathrm {B} \ $点から見た光源のまぶしさを表す指標で，
\[
\begin{eqnarray}
L&=&\frac {I_{\mathrm {\theta }}}{S} \ [ \mathrm {cd/m^{2}}] \\[ 5pt ] \end{eqnarray}
\] となります。

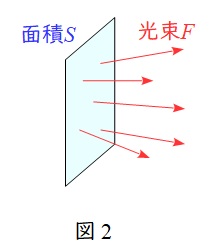
4.光束発散度$ \ M \ $
光源・反射面・透過面等の単位面積あたりから発散する光束をいい，面積$ \ S \ $から発散する光束を$ \ F \ $とすると，
\[
\begin{eqnarray}
M&=&\frac {F}{S} \ [ \mathrm {lm/m^{2}}] \\[ 5pt ] \end{eqnarray}
\] の関係があります。

5.照度$ \ E \ $，輝度$ \ L \ $及び光束発散度$ \ M \ $の関係
どの方向から見ても輝度$ \ L \ $の等しい面（完全拡散面）では，
\[
\begin{eqnarray}
M&=\pi L \\[ 5pt ] \end{eqnarray}
\] が成立し，ある反射面で照度$ \ E \ $で入射した光が反射率$ \ \rho \ $で反射したとすると，$ \ M=\rho E \ $となるため，
\[
\begin{eqnarray}
\rho E &=\pi L \\[ 5pt ] \end{eqnarray}
\] の関係が成立します。

6.逆$ \ 2 \ $乗の法則
照度$ \ E \ $と光度$ \ I \ $と光源からの距離$ \ l \ $の間に，
\[
\begin{eqnarray}
E&=&\frac {I}{l^{2}} \\[ 5pt ] \end{eqnarray}
\] が成立するという法則です。

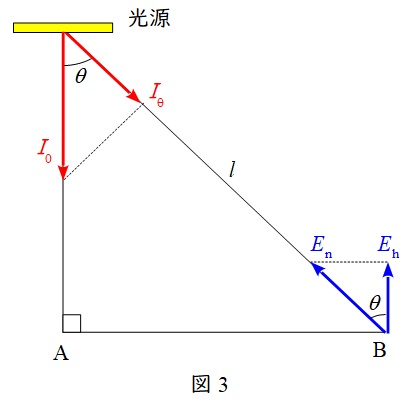
7.水平面照度
図3における$ \ E_{\mathrm {n}} \ $を法線照度，$ \ E_{\mathrm {h}} \ $を水平面照度と言い，以下のような関係があります。
\[
\begin{eqnarray}
E_{\mathrm {n}}&=&\frac {I_{\theta }}{l^{2}} \\[ 5pt ] E_{\mathrm {h}}&=&E_{\mathrm {\mathrm {n}}}\cos\theta \\[ 5pt ] &=&\frac {I_{\theta }\cos\theta }{l^{2}} \\[ 5pt ] \end{eqnarray}
\] ※　ランベルトの余弦法則は$ \ E_{\mathrm {h}}=E_{\mathrm {\mathrm {n}}}\cos \theta \ $のことを指します。

【解答】

(1)解答：ト
題意より解答候補は，（ニ）$ \ \displaystyle L=\frac {\rho I_{\mathrm {n}}}{\mathrm {d}S} \ $，（ヘ）$ \ \displaystyle L=\frac {\rho E}{\mathrm {d}S} \ $，（ト）$ \ \displaystyle L=\frac {\mathrm {d} I_{\mathrm {n}}}{\mathrm {d}S} \ $，になると思います。
ワンポイント解説「3.輝度$ \ L \ $」の通り，輝度は単位面積あたりの光度で表されるので，$ \ \displaystyle L=\frac {\mathrm {d} I_{\mathrm {n}}}{\mathrm {d}S} \ $が適切となります。

(2)解答：ヨ
題意より解答候補は，（チ）ラドルクス$ \ \left[ \mathrm {rlx} \right] \ $，（ワ）トロランド$ \ \left[ \mathrm {td} \right] \ $，（ヨ）カンデラ毎平方メートル$ \ \left[ \mathrm {cd/m^{2}} \right] \ $，になると思います。
ワンポイント解説「3.輝度$ \ L \ $」の通り，輝度の単位はカンデラ毎平方メートル$ \ \left[ \mathrm {cd/m^{2}} \right] \ $となります。

(3)解答：イ
題意より解答候補は，（イ）$ \ \mathrm {d}S\cdot \cos \theta \ $，（ロ）$ \ \mathrm {d}S\cdot \sin \theta \ $，（ホ）$ \ \mathrm {d}S\cdot \tan \theta \ $，になると思います。
ワンポイント解説「3.輝度$ \ L \ $」及び「7.水平面照度」の通り，法線より斜め$ \ \theta \ $方向から見た投影面積は，
\[
\begin{eqnarray}
\mathrm {d}S_{\mathrm {\theta }}&=&\mathrm {d}S\cdot \cos \theta \\[ 5pt ] \end{eqnarray}
\] となります。

(4)解答：ハ
題意より解答候補は，（ハ）均等拡散面，（リ）完全反射面，（ヲ）均等反射面，になると思います。
ワンポイント解説「5.照度$ \ E \ $，輝度$ \ L \ $及び光束発散度$ \ M \ $の関係」の通り，どの方向から見ても輝度の等しい面を均等拡散面といいます。

(5)解答：ル
題意より解答候補は，（ヌ）$ \ \pi E=\rho L \ $，（ル）$ \ \rho E=\pi L \ $，（カ）$ \ \rho \pi E=L \ $，になると思います。
ワンポイント解説「5.照度$ \ E \ $，輝度$ \ L \ $及び光束発散度$ \ M \ $の関係」の通り，均等拡散面において，照度$ \ E \ $と輝度$ \ L \ $との間には，
\[
\begin{eqnarray}
\rho E &=\pi L \\[ 5pt ] \end{eqnarray}
\] となる関係があります。