Contents
【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,食塩電解に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
食塩電解は食塩水を電解して塩素,水酸化ナトリウム(苛性ソーダ),水素を得る工業電解プロセスであり,全反応式は以下で表される。
\[
\begin{eqnarray}
2 \ \mathrm {NaCl} \ + \ 2 \ \mathrm {H_{2}O} \ &→& \ \mathrm {Cl_{2}} \ + \ \mathrm {H_{2}} \ + \ \fbox { (1) } \\[ 5pt ]
\end{eqnarray}
\]
現在,国内で行われているイオン交換膜法では,\( \ \mathrm {Na^{+}} \ \)の選択透過性のある密隔膜(イオン交換膜)を隔膜として利用し,アノードには寸法安定性電極,カソードにはニッケル系の電極が用いられ,理論分解電圧は\( \ 2.3 \ \mathrm {V} \ \),実際のセル電圧は\( \ 3.0~5.0 \ \mathrm {V} \ \)である。
電解槽のセル電圧を下げるためには,電極反応や電解槽の内部抵抗などが原因のセル電圧の上昇を小さくしなければならない。食塩電解の電極反応はターフェルの式に従う。したがって,通常時の電極電位と平衡電位の差である過電圧は電流が大きくなると,\( \ \fbox { (2) } \ \)に比例して大きくなる。内部抵抗は電解質の抵抗によるものが支配的である。この電解質の抵抗は電解液である食塩水や水酸化ナトリウムやイオン交換膜などの電解質のイオン抵抗である。内部抵抗を小さく,すなわちイオン伝導度を高くするためには電解質の濃度を高く維持する必要がある。このとき,食塩水や水酸化ナトリウムなどの強電解質の濃度あたりの伝導率であるモル伝導率は,イオン間の相互作用により濃度が高くなると\( \ \fbox { (3) } \ \)。
電解槽に加える電力は電流と電圧の積で表すことができ,電気化学反応も化学熱力学的な項,ファラデーの法則に基づく電流項,ネルンスト式で表される電圧項,それぞれ理論的な値が存在するので,電解槽のエネルギー変換効率は化学熱力学に基づく理論効率,電流効率と電圧効率の積で表される。
今,電極面積\( \ 2 \ \mathrm {m^{2}} \ \)の食塩電解セルを\( \ 2 \ \)時間運転した。このときのセル電圧が\( \ 3.3 \ \mathrm {V} \ \),電流密度が\( \ 6 \ \mathrm {kA / m^{2} } \ \),電流効率が\( \ 96 \ \mathrm {%} \ \)で一定であった。この間の電解セルの電圧効率は\( \ \fbox { (4) } \ \mathrm {%} \ \),標準状態換算での塩素の生産量は\( \ \fbox { (5) } \ \mathrm {kL} \ \)である。なお,ファラデー定数は\( \ 26.80 \ \mathrm {A\cdot h / mol} \ \),気体の標準状態の体積を\( \ 22.4 \ \mathrm {L / mol} \ \)とする。
〔問5の解答群〕
\[
\begin{eqnarray}
&(イ)& 変わらない &(ロ)& 2\mathrm {NaOH} &(ハ)& 2\mathrm {NaO} \\[ 5pt ]
&(ニ)& 小さくなる &(ホ)& \mathrm {NaOH} &(ヘ)& 大きくなる \\[ 5pt ]
&(ト)& 19.3 &(チ)& 69.7 &(リ)& 66.9 \\[ 5pt ]
&(ヌ)& 電流の対数 &(ル)& 電流の指数 &(ヲ)& 72.6 \\[ 5pt ]
&(ワ)& 10.0 &(カ)& 電流 &(ヨ)& 9.63 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
食塩電解に関する問題です。
\( \ 3 \ \)種ではまず出題されないレベルの難解な問題であったかと思います。
ほとんどの受験生が苦戦した問題であると思いますが,合格基準に到達するためには,本問の場合は(1)ともう一つは正答しておきたいところです。
1.イオン交換膜法による食塩電解
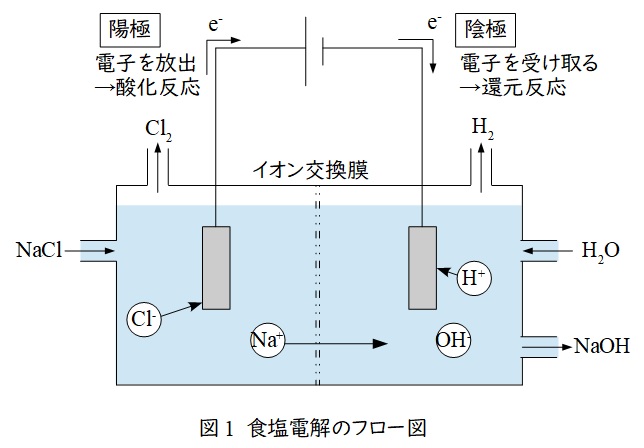
イオン交換膜法は最もポピュラーに使用されている方法で,図1のようなフローとなります。イオン交換膜はナトリウムイオン\( \ \mathrm {Na}^{+} \ \)のみが通過する構造となっています。また陽極と陰極の反応式は以下の通りとなります。
\[
\begin{eqnarray}
陽極&:&2\mathrm {Cl}^{-} \ → \ \mathrm {Cl_{2}} \ + \ 2\mathrm {e}^{-} \\[ 5pt ]
陰極&:&2\mathrm {Na}^{+} \ + \ 2\mathrm {H}^{+} \ + \ 2\mathrm {OH}^{-} \ + \ 2\mathrm {e}^{-} \ → \ \mathrm {H_{2}} \ + \ 2\mathrm {NaOH} \\[ 5pt ]
全体&:&2\mathrm {NaCl} \ + \ 2\mathrm {H_{2}O} \ → \ \mathrm {Cl_{2}} \ + \ \mathrm {H_{2}} \ + \ 2\mathrm {NaOH} \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(1)解答:ロ
題意より解答候補は,(ロ)\( \ 2\mathrm {NaOH} \ \),(ハ)\( \ 2\mathrm {NaO} \ \),(ホ)\( \ \mathrm {NaOH} \ \),になると思います。
ワンポイント解説「1.イオン交換膜法による食塩電解」の通り,生成される水酸化ナトリウム(苛性ソーダ)は\( \ 2\mathrm {NaOH} \ \)となります。
(化学反応式を覚えていなくても,反応式の原子数比較で正答を導けば大丈夫です。)
(2)解答:ヌ
題意より解答候補は,(ヌ)電流の対数,(ル)電流の指数,(カ)電流,になると思います。
ターフェルの式は,過電圧を\( \ \eta \ \),電流を\( \ I \ \),定数を\( \ a \ \),\( \ b \ \)(ターフェル傾斜)とすると,
\[
\begin{eqnarray}
\eta &=&a+b \log I \\[ 5pt ]
\end{eqnarray}
\]
で表され,電流の対数に比例します。
ターフェルの式は化学分野の電極の反応における専門的な内容なので,本空欄は電験としては捨て問として良いかと思います。
(3)解答:ニ
題意より解答候補は,(イ)変わらない,(ニ)小さくなる,(ヘ)大きくなる,になると思います。
モル伝導率とは単位モルあたりの伝導率のことであり,濃度が高くなるとモル伝導率は小さくなります。
(4)解答:チ
理論分解電圧は反応が進むために必要な最小限の電圧であり,本問においては理論分解電圧が\( \ 2.3 \ \mathrm {V} \ \),実際のセル電圧が\( \ 3.3 \ \mathrm {V} \ \)であるから,電圧効率\( \ \eta _{\mathrm {v}} \ \)は,
\[
\begin{eqnarray}
\eta _{\mathrm {v}} &=&\frac {2.3}{3.3} \\[ 5pt ]
&≒&0.697 → 69.7 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヨ
電極面積\( \ S=2 \ \mathrm {[m^{2}]} \ \),電流密度\( \ J=6 \ \mathrm {[kA / m^{2} ]} \ \),運転時間\( \ t=2 \ \mathrm {[h]} \ \),電流効率\( \ \eta _{\mathrm {i}}=96 \ \mathrm {[%]} \ \)であるから,反応に使用された電気量\( \ Q \ \mathrm {[kA\cdot h]} \ \)は,
\[
\begin{eqnarray}
Q &=&JSt\eta _{\mathrm {i}} \\[ 5pt ]
&=&6\times 2\times 2 \times 0.96 \\[ 5pt ]
&=&23.04 \ \mathrm {[kA\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
となる。ファラデー定数\( \ F=26.80 \ \mathrm {[A\cdot h / mol]} \ \)であり,ワンポイント解説「1.イオン交換膜法による食塩電解」の陽極の反応式より,電子\( \ 2 \ \mathrm {[mol]} \ \)に対して塩素\( \ 1 \ \mathrm {[mol]} \ \)が生産されるので,塩素の生産量\( \ V \ \mathrm {[kL]} \ \)は,
\[
\begin{eqnarray}
V &=&\frac {Q}{F}\times \frac {1}{2}\times 22.4 \\[ 5pt ]
&=&\frac {23.04\times 10^{3}}{26.80}\times \frac {1}{2}\times 22.4 \\[ 5pt ]
&≒&9.63\times 10^{3} \ \mathrm {[L]} → 9.63 \ \mathrm {[kL]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは