《機械》〈照明〉[R03:問6]グローブ照明器具における各諸量の導出に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，グローブ照明器具に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

乳白ガラスでできたグローブ（球体，半径$ \ r \ \mathrm {[m]} \ $）がある。グローブの中心には点光源（全光束$ \ F_{\mathrm {p}} \ \mathrm {[lm]} \ $）が置かれている。グローブの内側と外側の表面はともに均等拡散面である。点光源を発してグローブの内側表面に入射した光は，一部は反射され，残りは乳白ガラスに進入する。なお，乳白ガラスの厚みは無視でき，乳白ガラスの反射率及び透過率はそれぞれ$ \ \rho \ $及び$ \ \tau \ $とする。

また，グローブの内側表面で反射された光はグローブ内を進行して内側表面のどこかに再び入射し，そこで一部は反射され，残りは乳白ガラスに進入する。光はこのような過程をグローブ内で繰り返すが，グローブの内側表面で反射された光が点光源に吸収されることはないものとする。なお，円周率は$ \ \pi \ $とする。

以上の諸量を用いて，グローブから外部に放射される全光束$ \ F_{\mathrm {s}} \ $は$ \ \fbox {　（１）　} \ \mathrm {[lm]} \ $で表される。また$ \ F_{\mathrm {s}} \ $を用いて，グローブの光度$ \ I \ $は$ \ \fbox {　（２）　} \ \mathrm {[cd]} \ $，光束発散度$ \ M \ $は$ \ \fbox {　（３）　} \ \mathrm {[lm / m^{2}]} \ $で表される。

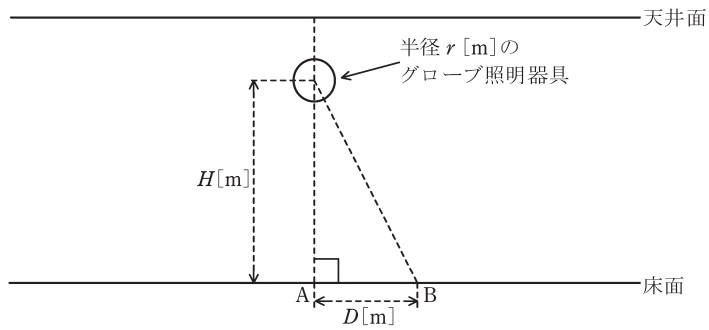
次に，図に示すように，このグローブ照明器具を部屋の天井面からつるし，部屋の照明を行った。グローブ中心真下の床面上の位置$ \ \mathrm {A} \ $点からグローブ中心までの高さは$ \ H \ \mathrm {[m]} \ $で，$ \ H≫r \ $である。また，$ \ \mathrm {A} \ $点から床面上の$ \ \mathrm {B} \ $点までの距離は$ \ D \ \mathrm {[m]} \ $である。なお，この部屋にはこのグローブ照明器具以外に光源はなく，天井，床，壁など，周囲からの反射光や入射光の影響はないものとする。

$ \ \mathrm {B} \ $点における水平面照度$ \ E_{\mathrm {h}} \ $はグローブの光度$ \ I \ $を用いて$ \ \fbox {　（４）　} \ \mathrm {[lx]} \ $で表される。また，$ \ \mathrm {B} \ $点からグローブの中心を見たときの輝度$ \ L \ $は光束発散度$ \ M \ $を用いて$ \ \fbox {　（５）　} \ \mathrm {[cd / m^{2}]} \ $となる。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {3F_{\mathrm {s}}}{4\pi }　　　　　&（ロ）&　\frac {F_{\mathrm {s}}}{2\pi }　　　　　&（ハ）&　\pi M \\[ 5pt ] &（ニ）&　\frac {I}{\sqrt {H^{2}+D^{2}}}　　　　　&（ホ）&　\frac {F_{\mathrm {s}}}{4\pi }　　　　　&（ヘ）&　\frac {F_{\mathrm {s}}}{2\pi r^{2}} \\[ 5pt ] &（ト）&　\frac {F_{\mathrm {p}}}{1-\rho }　　　　　&（チ）&　\frac {F_{\mathrm {s}}}{4\pi r^{2}}　　　　　&（リ）&　\frac {3F_{\mathrm {s}}}{4\pi r^{2}} \\[ 5pt ] &（ヌ）&　\frac {M}{\pi }　　　　　&（ル）&　\frac {\tau \rho F_{\mathrm {p}}}{1-\rho }　　　　　　　&（ヲ）&　\frac {\tau F_{\mathrm {p}}}{1-\rho } \\[ 5pt ] &（ワ）&　\frac {HI}{\left( H^{2}+D^{2} \right) ^{\frac {3}{2}}}　　　　　&（カ）&　\frac {M}{\pi r^{2}}　　　　　&（ヨ）&　\frac {DI}{\left( H^{2}+D^{2} \right) ^{\frac {3}{2}}} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

照明器具による光度や光束発散度，照度等の導出に関する問題です。
$ \ 2 \ $種一次試験には珍しく計算問題が出題され，受験生を苦しめたのではないかと思われる問題です。
今年の傾向からすると今後は計算問題も出題される可能性があるため，種々の基本公式は理解しておくようにしましょう。

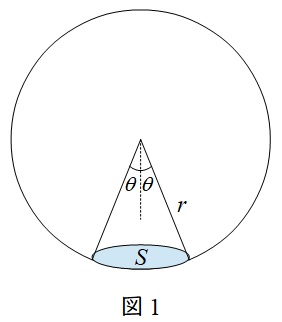
1.立体角の定義
図1のように球体があり，半径$ \ r \ \mathrm {[m]} \ $の錐体が球面を切り取った時の面積を$ \ S \ \mathrm {[m^{2}]} \ $とすると，立体角$ \ \omega \ \mathrm {[sr]} \ $は，
\[
\begin{eqnarray}
\omega &=&\frac {S}{r^{2}} \\[ 5pt ] \end{eqnarray}
\] であり，平面角$ \ \theta \ \mathrm {[rad]} \ $で表すと，
\[
\begin{eqnarray}
\omega &=&2\pi \left( 1-\cos \theta \right) \\[ 5pt ] \end{eqnarray}
\] となります。球全体の立体角は$ \ \theta = \pi \ $の時であり，$ \ \omega =4\pi \ $となります。

2.光度$ \ I \ $
ある方向に向かう光束$ \ F \ $を立体角$ \ \omega \ $で割ったものが光度$ \ I \ $となります。
\[
\begin{eqnarray}
I &=&\frac {\Delta F}{\Delta \omega } \\[ 5pt ] \end{eqnarray}
\]

3.光束発散度$ \ M \ $
光源・反射面・透過面等の単位面積あたりから発散する光束をいい，面積$ \ S \ $から発散する光束を$ \ F \ $とすると，
\[
\begin{eqnarray}
M&=&\frac {F}{S} \ [ \mathrm {lm/m^{2}}] \\[ 5pt ] \end{eqnarray}
\] の関係があります。

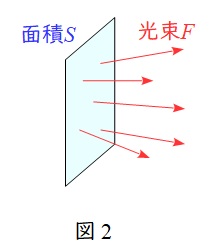
4.輝度$ \ L \ $
図3に示すように，$ \ \mathrm {B} \ $点から見た輝度は$ \ \mathrm {B} \ $点から見た光源のまぶしさを表す指標で，$ \ \mathrm {B} \ $点から照明を見た投影面積を$ \ S \ $とすると，
\[
\begin{eqnarray}
L&=&\frac {I_{\mathrm {\theta }}}{S} \ [ \mathrm {cd/m^{2}}] \\[ 5pt ] \end{eqnarray}
\] で求められます。

5.逆$ \ 2 \ $乗の法則
照度$ \ E \ $と光度$ \ I \ $と光源からの距離$ \ l \ $の間に，
\[
\begin{eqnarray}
E&=&\frac {I}{l^{2}} \\[ 5pt ] \end{eqnarray}
\] が成立するという法則です。

6.水平面照度
図4における$ \ E_{\mathrm {n}} \ $を法線照度，$ \ E_{\mathrm {h}} \ $を水平面照度と言い，以下のような関係があります。
\[
\begin{eqnarray}
E_{\mathrm {n}}&=&\frac {I_{\theta }}{l^{2}} \\[ 5pt ] E_{\mathrm {h}}&=&E_{\mathrm {\mathrm {n}}}\cos\theta \\[ 5pt ] &=&\frac {I_{\theta }\cos\theta }{l^{2}} \\[ 5pt ] \end{eqnarray}
\] ※　ランベルトの余弦法則は$ \ E_{\mathrm {h}}=E_{\mathrm {\mathrm {n}}}\cos \theta \ $のことを言います。

7.等比数列の和（数学）
初項が$ \ a \ $，公比が$ \ r \ $の等比数列，
\[
\begin{eqnarray}
a，ar，ar^{2}，\cdots ，ar^{n-1} \\[ 5pt ] \end{eqnarray}
\] があるときその和$ \ S_{\mathrm {n}} \ $は，
\[
\begin{eqnarray}
S_{\mathrm {n}}&=&a+ar+ar^{2}+\cdots +ar^{n-1} \ 　・・・・・・・・・・　①　\\[ 5pt ] \end{eqnarray}
\] となります。両辺$ \ r \ $倍すると，
\[
\begin{eqnarray}
rS_{\mathrm {n}}&=&ar+ar^{2}+ar^{3}+\cdots +ar^{n}　・・・・・・・・・・　②　 \\[ 5pt ] \end{eqnarray}
\] となるので，$ \ ①-② \ $より，
\[
\begin{eqnarray}
\left( 1-r\right) S_{\mathrm {n}}&=&a-ar^{n}　\\[ 5pt ] S_{\mathrm {n}}&=&\frac {a\left( 1-r^{n}\right) }{1-r}　\\[ 5pt ] \end{eqnarray}
\] で求められます。$ \ r ＜ 1 \ $であると仮定して$ \ n → \infty \ $であるとすると，
\[
\begin{eqnarray}
S_{\infty}&=&\frac {a}{1-r}　\\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ヲ
乳白ガラスの反射率及び透過率が$ \ \rho \ $及び$ \ \tau \ $であるので，全光束$ \ F_{\mathrm {p}} \ \mathrm {[lm]} \ $の点光源によりグローブから外部に放射される全光束$ \ F_{\mathrm {s}} \ $は，
\[
\begin{eqnarray}
F_{\mathrm {s}}&=&\tau F_{\mathrm {p}}+\tau \rho F_{\mathrm {p}}+\tau \rho ^{2} F_{\mathrm {p}}+\cdots \\[ 5pt ] \end{eqnarray}
\] となる。上式は，初項が$ \ \tau F_{\mathrm {p}} \ $，公比が$ \ \rho \ $の等比数列であるから，ワンポイント解説「7.等比数列の和（数学）」の通り計算すると，
\[
\begin{eqnarray}
F_{\mathrm {s}}&=&\frac {\tau F_{\mathrm {p}}}{1-\rho } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ホ
ワンポイント解説「2.光度$ \ I \ $」の通り，グローブの光度$ \ I \ \mathrm {[cd]} \ $は，立体角が$ \ 4\pi \ $であるから，
\[
\begin{eqnarray}
I&=&\frac {F_{\mathrm {s}}}{4\pi } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：チ
グローブの表面積$ \ S \ \mathrm {[m^{2}]} \ $は，
\[
\begin{eqnarray}
S&=&4\pi r^{2} \\[ 5pt ] \end{eqnarray}
\] であるから，光束発散度$ \ M \ \mathrm {[lm / m^{2}]} \ $は，ワンポイント解説「3.光束発散度$ \ M \ $」の通り，
\[
\begin{eqnarray}
M&=&\frac {F_{\mathrm {s}}}{S} \\[ 5pt ] &=&\frac {F_{\mathrm {s}}}{4\pi r^{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ワ
ワンポイント解説「6.水平面照度」の通り，$ \ \mathrm {B} \ $点における水平面照度$ \ E_{\mathrm {h}} \ \mathrm {[lx]} \ $は，
\[
\begin{eqnarray}
E_{\mathrm {h}}&=&\frac {I\cos\theta }{l^{2}} \\[ 5pt ] &=&\frac {\displaystyle I\cdot \frac {H}{\sqrt {D^{2}+H^{2}}}}{D^{2}+H^{2}} \\[ 5pt ] &=&\frac {HI}{\left( H^{2}+D^{2} \right) ^{\frac {3}{2}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヌ
ワンポイント解説「4.輝度$ \ L \ $」の通り，$ \ \mathrm {B} \ $点からグローブの中心を見たときの輝度$ \ L \ $は，
\[
\begin{eqnarray}
L&=&\frac {I}{\pi r^{2}} \\[ 5pt ] &=&\frac {\displaystyle \frac {F_{\mathrm {s}}}{4\pi }}{\pi r^{2}} \\[ 5pt ] &=&\frac {F_{\mathrm {s}}}{4\pi r^{2}}\cdot \frac {1}{\pi } \\[ 5pt ] &=&M\cdot \frac {1}{\pi } \\[ 5pt ] &=&\frac {M}{\pi } \\[ 5pt ] \end{eqnarray}
\] と求められる。