《機械》〈パワーエレクトロニクス〉[R06:問4]昇圧チョッパの回路と出力に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，昇圧チョッパに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

昇圧チョッパは，$ \ \fbox {　（１）　} \ $に示す図のようにスイッチ$ \ \mathrm {S} \ $，ダイオード，インダクタ$ \ \mathrm {L} \ $，キャパシタ$ \ \mathrm {C} \ $からなる回路が，直流電圧$ \ V_{\mathrm {i}} \ \mathrm {[V]} \ $の電圧源と負荷抵抗$ \ \mathrm {R} \ $の間に接続されることで構成されている。ここで，スイッチ$ \ \mathrm {S} \ $を$ \ T \ \mathrm {[s]} \ $の周期でオン－オフを繰り返し，そのうちオンしている期間を$ \ T_{\mathrm {on}} \ \mathrm {[s]} \ $とすると，スイッチ$ \ \mathrm {S} \ $のデューティ比$ \ D \ $は，$ \ \fbox {　（２）　} \ $として表すことができる。スイッチ及びダイオードを含む全ての回路素子が理想的なものであり，キャパシタ$ \ \mathrm {C} \ $の静電容量が十分大きくキャパシタ電圧のリプルは無視できるものとする。インダクタ$ \ \mathrm {L} \ $に電流が連続的に流れている場合，デューティ比$ \ D \ $を用いると直流電圧$ \ V_{\mathrm {i}} \ \mathrm {[V]} \ $と，定常状態で負荷抵抗に印加される電圧$ \ V_{\mathrm {o}} \ \mathrm {[V]} \ $の関係を表す式は$ \ \fbox {　（３）　} \ $となる。ここで，インダクタ，キャパシタ，抵抗に流れる電流をそれぞれ$ \ i_{\mathrm {L}} \ \mathrm {[A]} \ $，$i_{\mathrm {C}} \ \mathrm {[A]} \ $，$i_{\mathrm {R}} \ \mathrm {[A]} \ $とし，それらの平均値をそれぞれ$ \ I_{\mathrm {L}} \ \mathrm {[A]} \ $，$I_{\mathrm {C}} \ \mathrm {[A]} \ $，$I_{\mathrm {R}} \ \mathrm {[A]} \ $とすると，$I_{\mathrm {R}}= \ \fbox {　（４）　} \ $，$I_{\mathrm {C}}= \ \fbox {　（５）　} \ $となる。

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　V_{\mathrm {o}}=\frac {1}{1-D}V_{\mathrm {i}}　　　　　&（ロ）&　0　　　　　&（ハ）&　\frac {D}{1-D}I_{\mathrm {L}} \\[ 5pt ] &（ニ）&　\frac {T_{\mathrm {on}}}{T}　　　　　&（ホ）&　\left( 1-D\right) I_{\mathrm {L}}　　　　　&（ヘ）&　V_{\mathrm {o}}=DV_{\mathrm {i}} \\[ 5pt ] &（ト）&　\frac {1}{1-D}I_{\mathrm {L}}　　　　　　　&（チ）&　D I_{\mathrm {L}}　　　　　&（リ）&　\frac {T-T_{\mathrm {on}}}{T} \\[ 5pt ] &（ヌ）&　V_{\mathrm {o}}=\frac {D}{1-D}V_{\mathrm {i}}　　　　　&（ル）&　\frac {T}{T_{\mathrm {on}}}　　　　　&（ヲ）&　\frac {T}{T-T_{\mathrm {on}}} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

昇圧チョッパの動作と出力電圧，電流に関する問題です。
電験二種においては二次試験でも出題される可能性がある内容です。
動作原理や出力電圧の導出等もしっかりと理解しておくようにして下さい。

1.降圧チョッパ
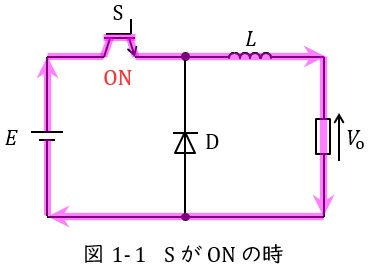
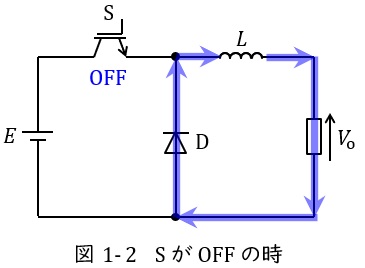
図1-1及び図1-2は降圧チョッパの例を示します。
スイッチ$ \ \mathrm {S} \ $がオンになると，図1-1のように電源からの電流はスイッチ$ \ \mathrm {S} \ $を通り，リアクトル$ \ L \ $側に電流が流れますが，ダイオード$ \ \mathrm {D} \ $は逆向きなので電流が流れません。
スイッチ$ \ \mathrm {S} \ $がオフになると，図1-2のように電源から電流は流れず，リアクトル$ \ L \ $に蓄えられているエネルギーから出力側と還流ダイオード$ \ \mathrm {D} \ $に電流が流れます。
したがって降圧チョッパの出力電圧の平均値$ \ V_{\mathrm {o}} \ $は，スイッチのオン時間を$ \ T_{\mathrm {on}} \ $，オフ時間を$ \ T_{\mathrm {off}} \ $とすると，
\[
\begin{eqnarray}
V_{\mathrm {o}}&=&\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}E \\[ 5pt ] \end{eqnarray}
\] で求められます。このとき，$ \ E \ $の係数
\[
\begin{eqnarray}
\gamma &=&\frac {T_{\mathrm {ON}}}{T_{\mathrm {ON}}+T_{\mathrm {OFF}}} \\[ 5pt ] \end{eqnarray}
\] を通流率といいます。

2.昇圧チョッパ
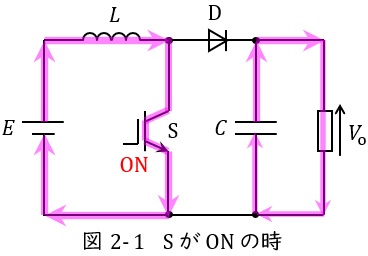
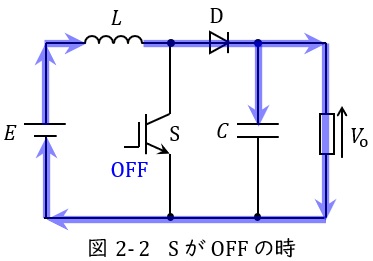
図2-1及び図2-2に昇圧チョッパの例を示します。
スイッチ$ \ \mathrm {S} \ $が$ \ \mathrm {ON} \ $時は図2-1のように導通し，電源$ \ E \ $からリアクトル$ \ L \ $にエネルギー$ \ EIT_{\mathrm {on}} \ $が蓄えられ，出力側はコンデンサ$ \ C \ $から電荷が供給されます。
スイッチ$ \ \mathrm {OFF} \ $時は図2-2のように導通し，リアクトル$ \ L \ $に蓄えられたエネルギー$ \ \displaystyle L\frac {\mathrm {d}i}{\mathrm {d}t}IT_{\mathrm {off}} \ $が放出されます。定常状態では蓄えられるエネルギーと放出するエネルギーが等しいので，
\[
\begin{eqnarray}
EIT_{\mathrm {on}}&=&L\frac {\mathrm {d}i}{\mathrm {d}t}IT_{\mathrm {off}} \\[ 5pt ] ET_{\mathrm {on}}&=&L\frac {\mathrm {d}i}{\mathrm {d}t}T_{\mathrm {off}} \\[ 5pt ] L\frac {\mathrm {d}i}{\mathrm {d}t}&=&\frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}E \\[ 5pt ] \end{eqnarray}
\] となります。また回路方程式は，
\[
\begin{eqnarray}
E+L\frac {\mathrm {d}i}{\mathrm {d}t}&=&V_{\mathrm {o}} \\[ 5pt ] \end{eqnarray}
\] となるので，
\[
\begin{eqnarray}
E+L\frac {\mathrm {d}i}{\mathrm {d}t}&=&V_{\mathrm {o}} \\[ 5pt ] E+\frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}E&=&V_{\mathrm {o}} \\[ 5pt ] V_{\mathrm {o}}&=&\frac {T_{\mathrm {on}}+T_{\mathrm {off}}}{T_{\mathrm {off}}}E \\[ 5pt ] \end{eqnarray}
\] となり，通流率$ \ \displaystyle \gamma =\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}} \ $を用いて表すと，
\[
\begin{eqnarray}
v_{\mathrm {0}} &=&\frac {T_{\mathrm {on}}+T_{\mathrm {off}}}{T_{\mathrm {off}}}E \\[ 5pt ] &=&\frac {\displaystyle \frac {T_{\mathrm {on}}+T_{\mathrm {off}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}}{\displaystyle \frac {T_{\mathrm {off}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}}E \\[ 5pt ] &=&\frac {1}{\displaystyle \frac {T_{\mathrm {on}}+T_{\mathrm {off}}-T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}}E \\[ 5pt ] &=&\frac {1}{\displaystyle 1-\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}}E \\[ 5pt ] &=&\frac {1}{\displaystyle 1-\gamma }E \\[ 5pt ] \end{eqnarray}
\] となります。

3.昇降圧チョッパ
スイッチ$ \ \mathrm {S} \ $がオンのとき，図3-1のように電源からの電流はスイッチ$ \ \mathrm {S} \ $を通り，リアクトル$ \ L \ $側にエネルギーが蓄えられますが，ダイオード$ \ \mathrm {D} \ $は逆向きなので電流が流れません。また，コンデンサ$ \ C \ $に蓄えられている電荷が出力側に流れます。
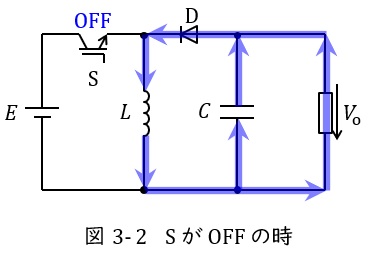
スイッチ$ \ \mathrm {S} \ $がオフになると，図3-2のように電源から電流は流れず，リアクトル$ \ L \ $に蓄えられていたエネルギーが放出され，コンデンサ$ \ C \ $と出力側に電流が流れます。
したがって，コンデンサ$ \ C \ $の容量が十分に大きければ，出力電流はほぼ一定の値となります。
定常状態においてはリアクトルに蓄えられるエネルギーと放出されるエネルギーが等しいので，スイッチ$ \ \mathrm {S} \ $のオン時間を$ T_{\mathrm {on}} \ $，オフ時間を$ T_{\mathrm {off}} \ $，出力電圧$ \ V_{\mathrm {0}} \ $とすると，
\[
\begin{eqnarray}
EIT_{\mathrm {on}} &=& V_{\mathrm {0}} IT_{\mathrm {off}} \\[ 5pt ] ET_{\mathrm {on}} &=&V_{\mathrm {0}} T_{\mathrm {off}} \\[ 5pt ] V_{\mathrm {0}} &=&\frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}E \\[ 5pt ] \end{eqnarray}
\] となり，通流率$ \ \displaystyle \gamma =\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}} \ $を用いて表すと，
\[
\begin{eqnarray}
v_{\mathrm {0}} &=&\frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}E \\[ 5pt ] &=&\frac {\displaystyle \frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}}{\displaystyle \frac {T_{\mathrm {off}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}}E \\[ 5pt ] &=&\frac {\displaystyle \frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}}{\displaystyle \frac {T_{\mathrm {on}}+T_{\mathrm {off}}-T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}}E \\[ 5pt ] &=&\frac {\displaystyle \frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}}{\displaystyle 1-\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}}E \\[ 5pt ] &=&\frac {\gamma }{\displaystyle 1-\gamma }E \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ワ
題意より解答候補は，（ワ）の回路図，（カ）の回路図，（ヨ）の回路図，になると思います。
ワンポイント解説「2.昇圧チョッパ」の通り，昇圧チョッパは（ワ）の回路図となります。（カ）は降圧チョッパ，（ヨ）は昇降圧チョッパです。

(2)解答：ニ
題意より解答候補は，（ニ）$ \ \displaystyle \frac {T_{\mathrm {on}}}{T} \ $，（リ）$ \ \displaystyle \frac {T-T_{\mathrm {on}}}{T} \ $，（ル）$ \ \displaystyle \frac {T}{T_{\mathrm {on}}} \ $，（ヲ）$ \ \displaystyle \frac {T}{T-T_{\mathrm {on}}} \ $，になると思います。
ワンポイント解説「1.降圧チョッパ」の通り，デューティ比（通流率）$ \ D \ $は$ \ \displaystyle \frac {T_{\mathrm {ON}}}{T_{\mathrm {ON}}+T_{\mathrm {OFF}}}=\frac {T_{\mathrm {on}}}{T} \ $となります。

(3)解答：イ
題意より解答候補は，（イ）$ \ \displaystyle V_{\mathrm {o}}=\frac {1}{1-D}V_{\mathrm {i}} \ $，（ヘ）$ \ \displaystyle V_{\mathrm {o}}=DV_{\mathrm {i}} \ $，（ヌ）$ \ \displaystyle V_{\mathrm {o}}=\frac {D}{1-D}V_{\mathrm {i}} \ $，になると思います。
ワンポイント解説「2.昇圧チョッパ」の通り，出力電圧$ \ V_{\mathrm {o}} \ \mathrm {[V]} \ $をデューティ比$ \ D \ $で表すと$ \ \displaystyle V_{\mathrm {o}}=\frac {1}{1-D}V_{\mathrm {i}} \ $となります。

(4)解答：ホ
題意より解答候補は，（ロ）$ \ 0 \ $，（ハ）$ \ \displaystyle \frac {D}{1-D}I_{\mathrm {L}} \ $，（ホ）$ \ \displaystyle \left( 1-D\right) I_{\mathrm {L}} \ $，（ト）$ \ \displaystyle \frac {1}{1-D}I_{\mathrm {L}} \ $，（チ）$ \ \displaystyle D I_{\mathrm {L}} \ $，になると思います。
ワンポイント解説「2.昇圧チョッパ」の通り，抵抗$ \ \mathrm {R} \ $に流れる電流はスイッチ$ \ \mathrm {S} \ $がオフのときと，オフの際にキャパシタ$ \ \mathrm {C} \ $に蓄えられた電荷がオンのときに放出する分です。したがって，平均値はオフの際にリアクトルに流れる電流の平均値と等しいため，
\[
\begin{eqnarray}
I_{\mathrm {R}} &=&\frac {T_{\mathrm {off}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}I_{\mathrm {L}} \\[ 5pt ] &=&\frac {T_{\mathrm {on}}+T_{\mathrm {off}}-T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}I_{\mathrm {L}} \\[ 5pt ] &=&1-\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}I_{\mathrm {L}} \\[ 5pt ] &=&\left( 1-D\right) I_{\mathrm {L}} \\[ 5pt ] \end{eqnarray}
\] となります。

(5)解答：ロ
題意より解答候補は，（ロ）$ \ 0 \ $，（ハ）$ \ \displaystyle \frac {D}{1-D}I_{\mathrm {L}} \ $，（ホ）$ \ \displaystyle \left( 1-D\right) I_{\mathrm {L}} \ $，（ト）$ \ \displaystyle \frac {1}{1-D}I_{\mathrm {L}} \ $，（チ）$ \ \displaystyle D I_{\mathrm {L}} \ $，になると思います。
ワンポイント解説「2.昇圧チョッパ」の通り，キャパシタ$ \ \mathrm {C} \ $にはオフの際に電荷が蓄えられ，オンの際に同量の電荷が放出するため，平均値は$ \ I_{\mathrm {C}}= 0 \ $となります。