《機械》〈照明〉[R07:問7]LEDランプの仕様や配光特性に関する空欄穴埋・計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★★（難しい）

次の文章は，電球形$ \ \mathrm {LED} \ $ランプの仕様に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

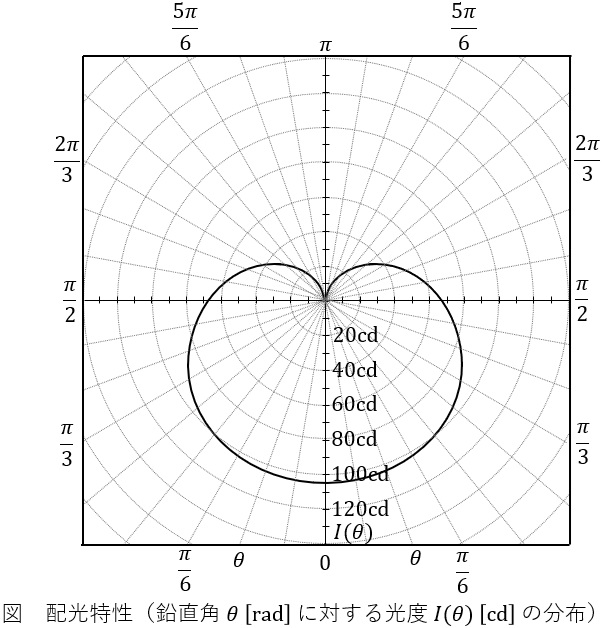
電球形$ \ \mathrm {LED} \ $ランプは省エネルギー性能に優れ，かつ長寿命で，水銀の使用もないことから，白熱電球および電球形蛍光ランプに替えて，普及が進みつつある。表は，ある電球形$ \ \mathrm {LED} \ $ランプの仕様の一部である。このランプの配光は対称配光であり，図のような鉛直配光特性（鉛直角$ \ \theta \ \mathrm {[rad]} \ $に対する光度$ \ I\left( \theta \right) \ \mathrm {[rad]} \ $の分布）を有している。

（a）表の数値から，このランプのエネルギー消費効率は$ \ \fbox {　（１）　} \ $であることがわかる。

（b）定格光束は全光束で表される。全光束は光源から発せられる光束の総和である。このランプの全光束$ \ \mathit {\Phi } \ $は図の配光特性から次式によって求めることができる。
\[
\begin{eqnarray}
\mathit {\Phi } &=& \ \fbox {　（２）　} \ =810\ \mathrm {lm} \\[ 5pt ] \end{eqnarray}
\] （c）色温度は光源の光色を表す指標で，その光源と等しい光色をもつ$ \ \fbox {　（３）　} \ $の絶対温度$ \ \mathrm {[K]} \ $で表される。光源の色度点が色度図上において$ \ \fbox {　（３）　} \ $の軌跡から離れている場合は相関色温度と呼ばれる。

（d）定格ランプ寿命は「既定の条件で点灯したとき，電球形$ \ \mathrm {LED} \ $ランプが定格光束の$ \ \fbox {　（４）　} \ $以上の光束を維持している期間」と定義されている。

（e）このランプを，室の床面から高さ$ \ 2.5 \ \mathrm {m} \ $の位置に，発光面頂部を鉛直下方に向けて設置する。室にはこのランプ以外に光源はなく，室外部からの入射光もない。また，室の天井面，床面，壁面，ランプの表面などにおける反射光の影響はないものとすると，ランプ直下の床面の照度は$ \ \fbox {　（５）　} \ $になる。

　　　　　　　　　　　　　　　　　　　表　ランプ仕様
\[
\begin{array}{|c|c|c|c|c|c|c|}
\hline
定格 & 定格 & 定格 & 定格光束 & 相関 & 平均演色 & 定格 \\
入力電圧 & 入力電流 & ランプ電力 & （全光束） & 色温度 & 評価数 & ランプ寿命 \\
& & （消費電力） & & & & \\
\hline
100 \ \mathrm {V} & 0.13 \ \mathrm {A} & 7.3 \ \mathrm {W} & 810 \ \mathrm {lm} & 5 \ 000 \ \mathrm {K} & \mathrm {Ra} \ 83 & 40 \ 000 \ \mathrm {h} \\
\hline
\end{array}
\]

〔問7の解答群〕
\[
\begin{eqnarray}
&（イ）&　黒体　　　　&（ロ）&　41.6 \ \mathrm {lx}　　　　　&（ハ）&　0.56 \\[ 5pt ] &（ニ）&　50 \ ％　　　　　&（ホ）&　90 \ ％　　　　　&（ヘ）&　標準抵抗器 \\[ 5pt ] &（ト）&　111 \ \mathrm {lm / W}　　　　　&（チ）&　2\pi \int _{0}^{\pi }I\left( \theta \right) \sin \theta \mathrm {d}\theta 　　　　　&（リ）&　70 \ ％ \\[ 5pt ] &（ヌ）&　9.01 \ \mathrm {mW / lm}　　　　　　&（ル）&　6.7 \ \mathrm {lx}　　　　　&（ヲ）&　\pi \int _{0}^{\pi }I\left( \theta \right) \sin \theta \mathrm {d}\theta \\[ 5pt ] &（ワ）&　2\pi \int _{0}^{\pi }I\left( \theta \right) \cos \theta \mathrm {d}\theta　　　　　&（カ）&　16.6 \ \mathrm {lx}　　　　　&（ヨ）&　標準電球のフィラメント \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

$ \ \mathrm {LED} \ $ランプの仕様や配光に関する問題です。
均等放射の光源が一般的であった電験の問題としてはかなり捻った問題が出題されました。積分の考え方をしっかりと理解していないと解けない空欄もあるため，受験生には大変厳しい問題であったかと思います。全問正解でなくても，$ \ 2\sim 3 \ $個の空欄が埋められれば十分合格圏内には到達できるかと思います。

1.エネルギー消費効率
エネルギー消費効率は発光効率等とも呼ばれ，$ \ 1 \ \mathrm {W} \ $あたりどれだけの明るさ$ \ \mathrm {[lm]} \ $を得られるかの効率であり，ランプの全光束を$ \ \mathit {\Phi } \ \mathrm {[lm]} \ $，消費電力を$ \ P \ \mathrm {[W]} \ $とすると，エネルギー消費効率$ \ \eta \ \mathrm {[lm / W]} \ $は，
\[
\begin{eqnarray}
\eta &=&\frac {\mathit {\Phi }}{P} \\[ 5pt ] \end{eqnarray}
\] で求められます。一般に$ \ \mathrm {LED} \ $のエネルギー消費効率は，電球の$ \ 10 \ $倍以上とされています。

2.光束$ \ F \ $
光源から出る可視光の量（エネルギー）で，単位は$ \ \mathrm {[lm]} \ $となります。
電磁気の分野の電束に似たようなイメージで良いです。

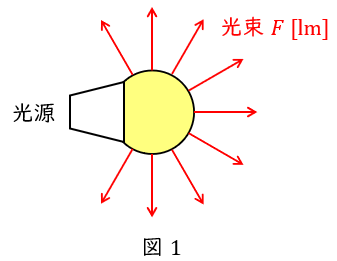
3.立体角の定義
図2のように球体があり，半径$ \ r \ \mathrm {[m]} \ $の錐体が球面を切り取った時の面積を$ \ S \ \mathrm {[m^{2}]} \ $とすると，立体角$ \ \omega \ \mathrm {[sr]} \ $は，
\[
\begin{eqnarray}
\omega &=&\frac {S}{r^{2}} \\[ 5pt ] \end{eqnarray}
\] であり，平面角$ \ \theta \ \mathrm {[rad]} \ $で表すと，
\[
\begin{eqnarray}
\omega &=&2\pi \left( 1-\cos \theta \right) \\[ 5pt ] \end{eqnarray}
\] となります。球全体の立体角は$ \ \theta = \pi \ $の時であり，$ \ \omega =4\pi \ $となります。

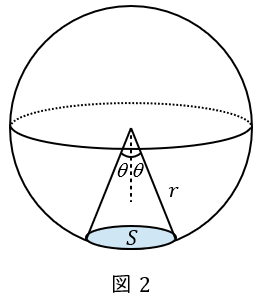
4.光度$ \ I \ $
ある方向に向かう光束$ \ F \ \mathrm {[lm]} \ $を立体角$ \ \omega \ \mathrm {[sr]} \ $で割ったもので，光度$ \ I \ \mathrm {[cd]} \ $を式で表すと，
\[
\begin{eqnarray}
I &=&\frac {\mathrm {d}F}{\mathrm {d}\omega } \\[ 5pt ] \end{eqnarray}
\] となります。

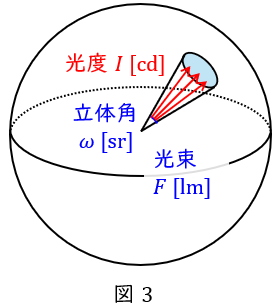
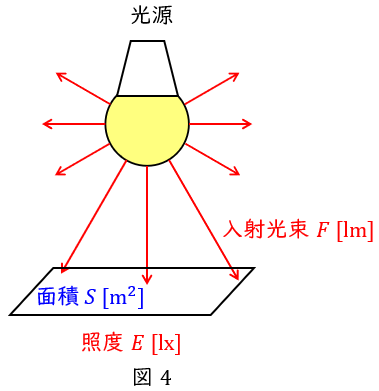
5.照度$ \ E \ $
単位面積あたりの光束で単位は$ \ \mathrm {[lx]} \ $で，図4のように光源から面積$ \ S \ \mathrm {[m^{2}]} \ $の面に入射する光束が$ \ F \ \mathrm {[lm]} \ $であるとき，平均照度$ \ E \ \mathrm {[lx]} \ $は，
\[
\begin{eqnarray}
E&=&\frac {F}{S} \\[ 5pt ] \end{eqnarray}
\] となります。
また，光源からある方向へ向かう光度が$ \ I \ \mathrm {[cd]} \ $であるとき，光源からの距離$ \ l \ \mathrm {[m]} \ $離れた垂直面の照度$ \ E \ \mathrm {[lx]} \ $は，
\[
\begin{eqnarray}
E&=&\frac {I}{l^{2}} \\[ 5pt ] \end{eqnarray}
\] と求められます。このように，一般に物理量が$ \ 2 \ $乗に反比例する法則を逆$ \ 2 \ $乗の法則といいます。

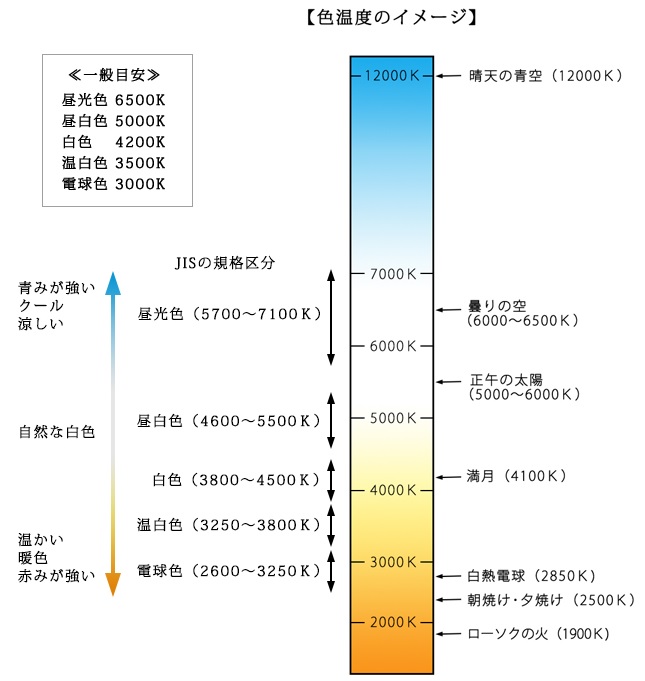
6.色温度
黒体を絶対零度として，温度と色の変化の関係を利用し、光色の変化を温度で表したものを言い，単位は$ \ \mathrm {[K]} \ $を用います。
一般的に暖色→白→青白→青となっていくほど，色温度は高くなります。

出典：マイクラフト　ＨＰ
http://www.my-craft.jp/html/aboutled/led_iroondo.html

【解答】

(1)解答：ト
題意より解答候補は，（ハ）$ \ 0.56 \ $，（ト）$ \ 111 \ \mathrm {lm / W} \ $，（ヌ）$ \ 9.01 \ \mathrm {mW / lm} \ $，になると思います。
ワンポイント解説「1.エネルギー消費効率」の通り，エネルギー消費効率$ \ \eta \ $は，ランプの全光束が$ \ 810 \ \mathrm {lm} \ $，消費電力が$ \ 7.3 \ \mathrm {W} \ $であることから，
\[
\begin{eqnarray}
\eta &=&\frac {810}{7.3} \\[ 5pt ] &≒&111 \ \mathrm {[lm / W]} \\[ 5pt ] \end{eqnarray}
\] と求められます。

(2)解答：チ
題意より解答候補は，（チ）$ \ \displaystyle 2\pi \int _{0}^{\pi }I\left( \theta \right) \sin \theta \mathrm {d}\theta \ $，（ヲ）$ \ \displaystyle \pi \int _{0}^{\pi }I\left( \theta \right) \sin \theta \mathrm {d}\theta \ $，（ワ）$ \ \displaystyle 2\pi \int _{0}^{\pi }I\left( \theta \right) \cos \theta \mathrm {d}\theta \ $，になると思います。
ワンポイント解説「4.光度$ \ I \ $」の通り，$ \ \theta \ $方向の光度$ \ I\left( \theta \right) \ $による光束$ \ \mathrm {d}\mathit {\Phi } \ $は，ワンポイント解説「3.立体角の定義」の通り立体角$ \ \omega =2\pi \left( 1-\cos \theta \right) \ $とすると，
\[
\begin{eqnarray}
\mathrm {d}\mathit {\Phi } &=&I\left( \theta \right) \mathrm {d}\omega \\[ 5pt ] \end{eqnarray}
\] となり，
\[
\begin{eqnarray}
\frac {\mathrm {d}\omega }{\mathrm {d}\theta } &=&2\pi \left\{ 0-\left( -\sin \theta \right) \right\} \\[ 5pt ] &=&2\pi \sin \theta \\[ 5pt ] \mathrm {d}\omega &=&2\pi \sin \theta \mathrm {d}\theta \\[ 5pt ] \end{eqnarray}
\] であることから，
\[
\begin{eqnarray}
\mathrm {d}\mathit {\Phi } &=&I\left( \theta \right) \mathrm {d}\omega \\[ 5pt ] &=&I\left( \theta \right) 2\pi \sin \theta \mathrm {d}\theta \\[ 5pt ] \end{eqnarray}
\] となるので，両辺積分すると，
\[
\begin{eqnarray}
\mathit {\Phi } &=&\int _{0}^{\pi }I\left( \theta \right) 2\pi \sin \theta \mathrm {d}\theta \\[ 5pt ] &=&2\pi \int _{0}^{\pi }I\left( \theta \right) \sin \theta \mathrm {d}\theta \\[ 5pt ] \end{eqnarray}
\] と求められます。

(3)解答：イ
題意より解答候補は，（イ）黒体，（ヘ）標準抵抗器，（ヨ）標準電球のフィラメント，になると思います。
ワンポイント解説「6.色温度」の通り，色温度は光源の光色を表す指標で，その光源と等しい光色をもつ黒体の絶対温度$ \ \mathrm {[K]} \ $で表されます。

(4)解答：リ
題意より解答候補は，（ニ）$ \ 50 \ ％ \ $，（ホ）$ \ 90 \ ％ \ $，（リ）$ \ 70 \ ％ \ $，になると思います。
一般にランプ寿命はランプが点灯不能になるまでの時間と光束維持率が$ \ 70 \ ％ \ $以下になるまでの時間の短い方の時間で決まります。

(5)解答：カ
題意より解答候補は，（ロ）$ \ 41.6 \ \mathrm {lx} \ $，（ル）$ \ 6.7 \ \mathrm {lx} \ $，（カ）$ \ 16.6 \ \mathrm {lx} \ $，になると思います。
問題図に与えられている配光特性より，鉛直下方における光度は$ \ I(0)=104 \ \mathrm {[cd]} \ $程度であるため，ランプ直下$ \ 2.5 \ \mathrm {m} \ $の床面の照度$ \ E \ \mathrm {[lx]} \ $は，ワンポイント解説「5.照度$ \ E \ $」の通り，
\[
\begin{eqnarray}
E &=&\frac {104}{2.5^{2}} \\[ 5pt ] &≒&16.6 \ \mathrm {[lx]} \\[ 5pt ] \end{eqnarray}
\] と求められます。