【問題】
【難易度】★★☆☆☆(やや易しい)
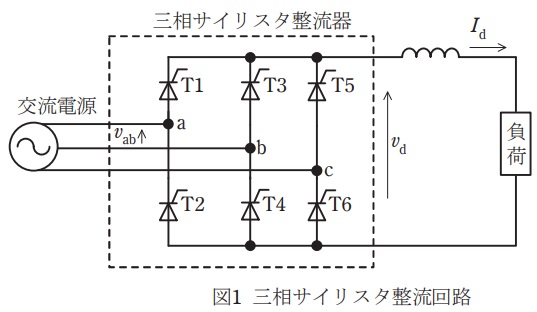
図1は三相サイリスタ整流回路であり,整流器のサイリスタに番号を付している。交流電源の電圧は三相対称正弦波で,線間電圧実効値を\( \ V \ \),相順は\( \ \mathrm {a}→\mathrm {b}→\mathrm {c} \ \)相とする。制御遅れ角\( \ \alpha \ \)で運転していて,直流回路のインダクタンスは十分に大きく直流電流\( \ I_{\mathrm {d}} \ \)は一定とし,重なり角,回路の損失などは無視できるものとする。回路の動作に関して,次の問に答えよ。
(1) ある時刻に整流器のサイリスタ \( \ \mathrm {T1} \ \)及び\( \ \mathrm {T6} \ \)がオンしていたとする。サイリスタは相順に従って電気角で\( \ 120° \ \)期間オンすることを考慮すると,電気角で\( \ 60° \ \)に相当する時間後にオンしているのはどの二つのサイリスタであるかを示せ。
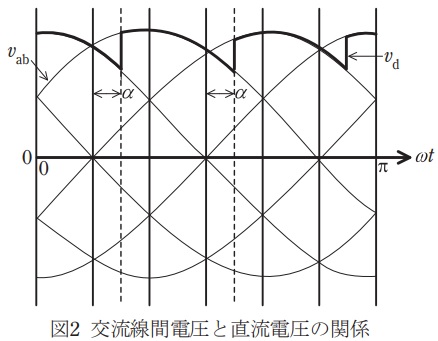
(2) 整流器を図2に示す制御遅れ角\( \ \alpha \ \)で運転したときに,直流電圧\( \ v_{\mathrm {d}} \ \)の平均値\( \ V_{\mathrm {d}} \ \)を表す式を,\( \ V \ \)及び\( \ \alpha \ \)を用いて示せ。
(3) 損失がないとしているので,整流器に入力される交流の有効電力\( \ P_{\mathrm {a}} \ \)と直流電力\( \ P_{\mathrm {d}} \ \)とは等しい。電力\( \ P_{\mathrm {a}} \ \)を表す式を\( \ V \ \),\( \ I_{\mathrm {d}} \ \)及び\( \ \alpha \ \)を用いて示せ。
(4) 電源に流れる線電流は,半サイクルで\( \ 120° \ \)通電で波高値\( \ I_{\mathrm {d}} \ \)の方形波であるので,この電流波形に含まれる基本波実効値\( \ I_{\mathrm {a1}} \ \)は\( \ \displaystyle \frac {\sqrt {6}}{\pi }I_{\mathrm {d}} \ \)である。電源の基本波の皮相電力\( \ S_{\mathrm {a}} \ \)を表す式を\( \ V \ \)及び\( \ I_{\mathrm {d}} \ \)を用いて示せ。
(5) 小問(3)と小問(4)から,電源からの基本波の遅れの無効電力\( \ Q_{\mathrm {a}} \ \)を表す式を\( \ V \ \),\( \ I_{\mathrm {d}} \ \)及び\( \ \alpha \ \)を用いて示せ。
(6) 小問(3)と小問(5)の結果は,負荷の電力を制御遅れ角\( \ \alpha \ \)で制御すると,付随して電源の無効電力が変化することを示している。今,負荷を純抵抗\( \ R \ \)とし,電源の無効電力がゼロである運転をしたとき,負荷の電力\( \ P_{\mathrm {d}}^{\prime } \ \)を表す式を\( \ V \ \)及び\( \ R \ \)を用いて示せ。
【ワンポイント解説】
三相サイリスタブリッジ整流回路に関する問題です。
令和\( \ 5 \ \)年は一次試験にも三相サイリスタブリッジ整流回路が出題され,過去の出題傾向からは有り得ないような出題方式でした。
本問は\( \ 1 \ \)種のパワーエレクトロニクスの問題としてはかなり解きやすい問題となりますので,ぜひ理解するようにして下さい。
1.三相サイリスタブリッジ整流回路の動作と出力電圧
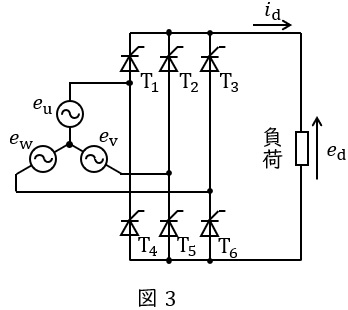
三相サイリスタブリッジ整流回路は図3に示す通り,三相交流回路から\( \ 6 \ \)つのサイリスタをブリッジ接続して直流を得る回路です。
各サイリスタは制御遅れ角\( \ \alpha \ \mathrm {[rad]} \ \)で,それぞれオンオフを\( \ \displaystyle \frac {2\pi }{3} \ \mathrm {[rad]} \ \)ずつ順番に繰り返します。例えば\( \ \mathrm {T_{1}} \ \)と\( \ \mathrm {T_{5}} \ \)がオンのときは,\( \ e_{\mathrm {u}} \ \)→\( \ \mathrm {T_{1}} \ \)→負荷→\( \ \mathrm {T_{5}} \ \)→\( \ e_{\mathrm {v}} \ \)と導通し,出力電圧は\( \ e_{\mathrm {u}}-e_{\mathrm {v}} \ \)となります。
ここで,電圧\( \ e_{\mathrm {u}} \ \)を基準とし,
\[
\begin{eqnarray}
e_{\mathrm {u}}&=& \sqrt {2}E\sin \omega t \\[ 5pt ]
e_{\mathrm {v}}&=& \sqrt {2}E\sin \left( \omega t-\frac {2}{3}\pi \right) \\[ 5pt ]
e_{\mathrm {w}}&=& \sqrt {2}E\sin \left( \omega t-\frac {4}{3}\pi \right) \\[ 5pt ]
\end{eqnarray}
\]
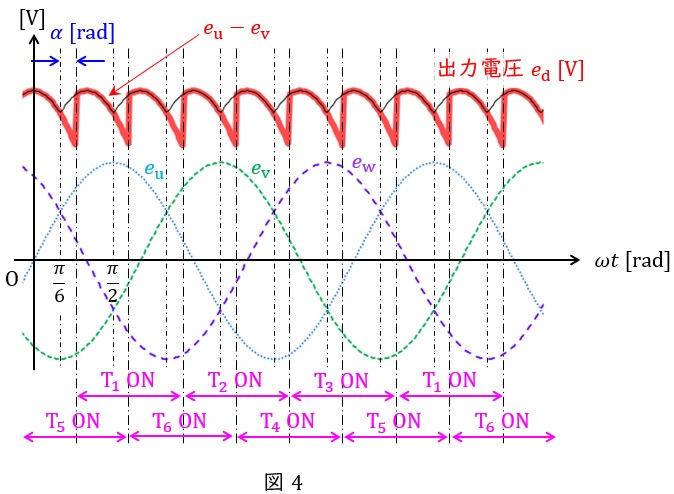
としたときの出力電圧波形は図4のようになり,出力電圧は\( \ \displaystyle \frac {\pi }{3} \ \mathrm {[rad]} \ \)毎の繰り返しとなります。したがって,出力電圧の平均値\( \ E_{\mathrm {d}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
E_{\mathrm {d}}&=& \frac {1}{\displaystyle \frac {\pi }{3}}\int ^{\frac {\pi }{2}+\alpha }_{\frac {\pi }{6}+\alpha }\left\{ \sqrt {2}E\sin \omega t-\sqrt {2}E\sin \left( \omega t-\frac {2}{3}\pi \right) \right\}\mathrm {d}\omega t \\[ 5pt ]
&=& \frac {3\sqrt {2}E}{\pi }\int ^{\frac {\pi }{2}+\alpha }_{\frac {\pi }{6}+\alpha }\left\{ \sin \omega t-\sin \left( \omega t-\frac {2}{3}\pi \right) \right\}\mathrm {d}\omega t \\[ 5pt ]
\end{eqnarray}
\]
となります。ここで和積の公式\( \ \displaystyle \sin A-\sin B=2\cos \frac {A+B}{2} \sin \frac {A-B}{2} \ \)より,
\[
\begin{eqnarray}
E_{\mathrm {d}}&=& \frac {3\sqrt {2}E}{\pi }\int ^{\frac {\pi }{2}+\alpha }_{\frac {\pi }{6}+\alpha }\left\{ 2\cos \left( \omega t-\frac {\pi }{3}\right) \sin \frac {\pi }{3} \right\}\mathrm {d}\omega t \\[ 5pt ]
&=& \frac {3\sqrt {2}E}{\pi }\int ^{\frac {\pi }{2}+\alpha }_{\frac {\pi }{6}+\alpha }\left\{ 2\cos \left( \omega t-\frac {\pi }{3}\right) \cdot \frac {\sqrt {3}}{2} \right\} \mathrm {d}\omega t \\[ 5pt ]
&=& \frac {3\sqrt {6}E}{\pi }\int ^{\frac {\pi }{2}+\alpha }_{\frac {\pi }{6}+\alpha } \cos \left( \omega t-\frac {\pi }{3}\right) \mathrm {d}\omega t \\[ 5pt ]
&=& \frac {3\sqrt {6}E}{\pi }\left[ \sin \left( \omega t-\frac {\pi }{3}\right)\right] ^{\frac {\pi }{2}+\alpha }_{\frac {\pi }{6}+\alpha } \\[ 5pt ]
&=& \frac {3\sqrt {6}E}{\pi }\left\{ \sin \left( \alpha +\frac {\pi }{6}\right) -\sin \left( \alpha -\frac {\pi }{6}\right)\right\} \\[ 5pt ]
&=& \frac {3\sqrt {6}E}{\pi }\cdot 2\cos \alpha \sin \frac {\pi }{6} \\[ 5pt ]
&=& \frac {3\sqrt {6}E}{\pi }\cdot 2\cos \alpha \cdot \frac {1}{2} \\[ 5pt ]
&=& \frac {3\sqrt {6}E}{\pi }\cos \alpha \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
【解答】
(1)\( \ \mathrm {T1} \ \)及び\( \ \mathrm {T6} \ \)がオンしていた\( \ 60° \ \)後にオンしているのはどの二つのサイリスタであるか
ワンポイント解説「1.三相サイリスタブリッジ整流回路の動作と出力電圧」図4の通りに各素子をオンオフを繰り返すので,図1の素子配置に合わせてグラフを記載すると図5のようになる。
図5より,\( \ \mathrm {T1} \ \)及び\( \ \mathrm {T6} \ \)がオンしていた\( \ 60° \ \)後にオンしているのは\( \ \mathrm {T3} \ \)及び\( \ \mathrm {T6} \ \)であることがわかる。

(2)直流電圧\( \ v_{\mathrm {d}} \ \)の平均値\( \ V_{\mathrm {d}} \ \)を表す式
ワンポイント解説「1.三相サイリスタブリッジ整流回路の動作と出力電圧」の通り,直流電圧\( \ v_{\mathrm {d}} \ \)の平均値\( \ V_{\mathrm {d}} \ \)は,\( \ \displaystyle E=\frac {V}{\sqrt {3}} \ \)を代入すれば同様に計算でき,
\[
\begin{eqnarray}
V_{\mathrm {d}}&=& \frac {3\sqrt {2}V}{\pi }\cos \alpha \\[ 5pt ]
&≒& 1.35V\cos \alpha \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)整流器に入力される交流の有効電力\( \ P_{\mathrm {a}} \ \)を表す式
題意より,整流器に入力される交流の有効電力\( \ P_{\mathrm {a}} \ \)は直流電力\( \ P_{\mathrm {d}} \ \)と等しく,直流電流\( \ I_{\mathrm {d}} \ \)は一定なので,
\[
\begin{eqnarray}
P_{\mathrm {a}}&=& P_{\mathrm {d}} \\[ 5pt ]
&=& V_{\mathrm {d}}I_{\mathrm {d}} \\[ 5pt ]
&=& \frac {3\sqrt {2}V}{\pi }\cos \alpha \cdot I_{\mathrm {d}} \\[ 5pt ]
&=& \frac {3\sqrt {2}}{\pi }VI_{\mathrm {d}}\cos \alpha \\[ 5pt ]
&≒& 1.35VI_{\mathrm {d}}\cos \alpha \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)電源の基本波の皮相電力\( \ S_{\mathrm {a}} \ \)を表す式
交流電源の線間電圧の実効値が\( \ V \ \),電流波形に含まれる基本波実効値\( \ I_{\mathrm {a1}}=\displaystyle \frac {\sqrt {6}}{\pi }I_{\mathrm {d}} \ \)であるため,電源の基本波の皮相電力\( \ S_{\mathrm {a}} \ \)は,
\[
\begin{eqnarray}
S_{\mathrm {a}}&=& \sqrt {3}VI_{\mathrm {a1}} \\[ 5pt ]
&=& \sqrt {3}V\frac {\sqrt {6}}{\pi }I_{\mathrm {d}} \\[ 5pt ]
&=& \frac {3\sqrt {2}}{\pi }VI_{\mathrm {d}} \\[ 5pt ]
&≒& 1.35VI_{\mathrm {d}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)電源からの基本波の遅れの無効電力\( \ Q_{\mathrm {a}} \ \)を表す式
\( \ {S_{\mathrm {a}}}^{2}={P_{\mathrm {a}}}^{2}+{Q_{\mathrm {a}}}^{2} \ \)の関係から,
\[
\begin{eqnarray}
Q_{\mathrm {a}}&=& \sqrt {{S_{\mathrm {a}}}^{2}-{P_{\mathrm {a}}}^{2}} \\[ 5pt ]
&=& \sqrt {\left( \frac {3\sqrt {2}}{\pi }VI_{\mathrm {d}}\right)^{2}-\left( \frac {3\sqrt {2}}{\pi }VI_{\mathrm {d}}\cos \alpha \right)^{2}} \\[ 5pt ]
&=& \frac {3\sqrt {2}}{\pi }VI_{\mathrm {d}}\sqrt {1-\cos ^{2}\alpha } \\[ 5pt ]
&=& \frac {3\sqrt {2}}{\pi }VI_{\mathrm {d}}\sin \alpha \\[ 5pt ]
&≒& 1.35VI_{\mathrm {d}}\sin \alpha \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(6)負荷を純抵抗\( \ R \ \)とし,電源の無効電力がゼロである運転をしたとき,負荷の電力\( \ P_{\mathrm {d}}^{\prime } \ \)を表す式
(5)解答式より,無効電力がゼロであるので,\( \ \sin \alpha =0 \ \)であり,\( \ \cos \alpha =1 \ \)となる。
したがって,問題図より,
\[
\begin{eqnarray}
P_{\mathrm {d}}^{\prime }&=& \frac {{V_{\mathrm {d}}}^{2}}{R} \\[ 5pt ]
\end{eqnarray}
\]
であり,(2)解答式より,
\[
\begin{eqnarray}
V_{\mathrm {d}}&=& \frac {3\sqrt {2}V}{\pi}\\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
P_{\mathrm {d}}^{\prime }&=& \frac {\displaystyle \left( \frac {3\sqrt {2}V}{\pi}\right) ^{2}}{R} \\[ 5pt ]
&=& \frac {18V^{2}}{\pi ^{2}R}\\[ 5pt ]
&≒& \frac {1.82V^{2}}{R}\\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん