《機械・制御》〈自動制御〉[H26:問4] フィードバック制御系に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

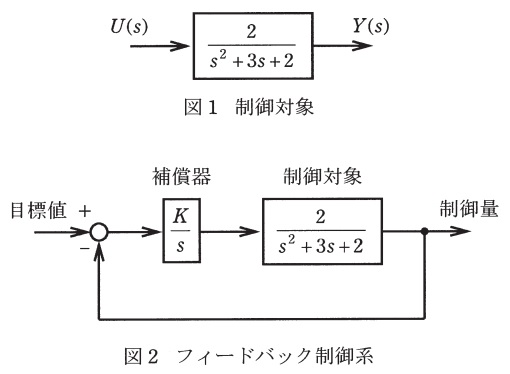
フィードバック制御系について，次の問に答えよ。ただし，図2中のゲイン\(K\)は正の実数とする。

(1)　図1に示す制御対象の入力\(U (s) \)に単位ステップ信号を入力したときの出力\(Y (s)\)の時間応答を求めよ。ただし，初期状態は零とする。

(2)　図2に示すフィードバック制御系の一巡周波数伝達関数のベクトル軌跡が複素平面の実軸を切るときの交点を求めよ。また，そのときの角周波数\(\omega _{0}\)を求めよ。

(3)　上記(2)の結果にナイキストの安定判別法を適用して，制御系を安定にするゲイン\(K\)の範囲を求めよ。

(4)　図2のフィードバック制御系の特性方程式を求めよ。

(5)　上記(4)で得た特性方程式のラウス表を示したのち，制御系を安定にするゲイン\(K\)の範囲を求めよ。

(6)　図2のフィードバック制御系が安定限界であるとき，閉ループ伝達関数の三つの極を求めよ。

【ワンポイント解説】

近年では少数派となった古典制御からの出題です。近年なかなか一種だとオーソドックスな問題は出題してくれず，本問のような比較的易しい問題は減ってきています。計算量は少なくないのでできるだけ早く解けるように何度も演習を繰り返しましょう。

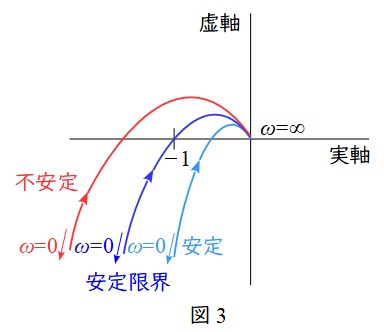
1.ナイキストの安定判別法
開ループ周波数伝達関数\( \ G_{0}( \mathrm {j}\omega ) \ \)が与えられている時，\( \ G_{0}( \mathrm {j}\omega ) \ \)が実軸と交わる点が，\( \ (-1，0 ) \ \)より右側ならば安定，左側ならば不安定，\( \ (-1，0 ) \ \)であれば安定限界となります。

2.ラウスの安定判別法
特性方程式\( \ a_{0}s^{n}+a_{1}s^{n-1}+a_{2}s^{n-2}+\cdots +a_{n-1}s+a_{n}=0 \ \)が与えられている時，ラウスの安定判別法による安定条件は，
\[
\begin{eqnarray}
&&1.　s^{n}，s^{n-1}，\cdots ，s^{1}，s^{0}の係数がすべて存在 \\[ 5pt ] &&2.　s^{n}，s^{n-1}，\cdots ，s^{1}，s^{0}の係数がすべて同符号 \\[ 5pt ] &&3.　ラウスの数表の値がすべて正であること \\[ 5pt ] \end{eqnarray}
\] です。ラウスの数表は下図のようになります。
\[
\begin{array}{c|ccc}
& 1列 & 2列 & 3列 \\
\hline
　1行　 & a_{0} & a_{2} & a_{4} & \cdots \\
　2行　 & a_{1} & a_{3} & a_{5} & \cdots \\
　3行　 & b_{1}=\frac {a_{1}a_{2}-a_{0}a_{3}}{a_{1}} & b_{2}=\frac {a_{1}a_{4}-a_{0}a_{5}}{a_{1}} & \cdots \\
　4行　 & c_{1}=\frac {b_{1}a_{3}-a_{1}b_{2}}{b_{1}} & c_{2}=\frac {b_{1}a_{5}-a_{1}b_{3}}{b_{1}} & \cdots \\
\vdots & \vdots & \vdots &
\end{array}
\]

【解答】

(1)図1に示す制御対象の入力\(U (s) \)に単位ステップ信号を入力したときの出力\(Y (s)\)の時間応答
単位ステップ応答のラプラス変換\(\displaystyle U (s) =\frac {1}{s}\)となるので，
\[
\begin{eqnarray}
Y (s) &=&\frac {2}{s^{2}+3s+2}\cdot \frac {1}{s} \\[ 5pt ] &=&\frac {2}{s\left( s+1\right)\left( s+2\right)} \\[ 5pt ] \end{eqnarray}
\] となるので，
\[
\begin{eqnarray}
Y (s) &=&\frac {\mathrm {A}}{s}+\frac {\mathrm {B}}{s+1}+\frac {\mathrm {C}}{s+2} \\[ 5pt ] \end{eqnarray}
\] と置くと，この式は，
\[
\begin{eqnarray}
Y (s) &=&\frac {\left( \mathrm {A}+\mathrm {B}+\mathrm {C}\right) s^{2} +\left( 3\mathrm {A}+2\mathrm {B}+\mathrm {C}\right) s+2\mathrm {A}}{s\left( s+1\right)\left( s+2\right)} \\[ 5pt ] \end{eqnarray}
\] となるので，係数比較すると，
\[
\begin{eqnarray}
\begin{cases}
\mathrm {A}+\mathrm {B}+\mathrm {C}=0 \\[ 5pt ] 3\mathrm {A}+2\mathrm {B}+\mathrm {C}=0 \\[ 5pt ] 2\mathrm {A}=2 \\[ 5pt ] \end{cases}
\end{eqnarray}
\] となるので，
\[
\begin{eqnarray}
\mathrm {A}=1，\mathrm {B}=-2，\mathrm {C}=1 \\[ 5pt ] \end{eqnarray}
\] と求められる。よって，
\[
\begin{eqnarray}
Y (s) &=&\frac {1}{s}-\frac {2}{s+1}+\frac {1}{s+2} \\[ 5pt ] \end{eqnarray}
\] となるので，ラプラス逆変換すると，
\[
\begin{eqnarray}
y (t) &=&1-2\mathrm {e}^{-t}+\mathrm {e}^{-2t} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)図2に示すフィードバック制御系の一巡周波数伝達関数のベクトル軌跡が複素平面の実軸を切るときの交点とそのときの角周波数\(\omega _{0}\)
図2に示すフィードバック制御系の一巡周波数伝達関数\(W (\mathrm {j}\omega )\)は，
\[
\begin{eqnarray}
W (\mathrm {j}\omega ) &=&\frac {K}{\mathrm {j}\omega }\cdot \frac {2}{-\omega ^{2} +3\mathrm {j}\omega +2} \\[ 5pt ] &=&\frac {2K}{-3\omega ^{2} +\mathrm {j}\left( -\omega ^{3} +2\omega \right) } \\[ 5pt ] \end{eqnarray}
\] となる。この\(W (\mathrm {j}\omega )\)において，虚部が零となる時の角周波数が\(\omega _{0}\)であるから，
\[
\begin{eqnarray}
-\omega_{0} ^{3} +2\omega_{0} &=&0 \\[ 5pt ] -\omega_{0} \left( \omega_{0} ^{2} -2\right) &=&0 \\[ 5pt ] \omega_{0} &=& 0，±\sqrt {2} \\[ 5pt ] \end{eqnarray}
\] となり，\(\omega _{0}＞0\)であるから，\(\omega _{0}=\sqrt {2}\)となる。この時の一巡周波数伝達関数は，
\[
\begin{eqnarray}
W (\mathrm {j}\sqrt {2} ) &=&\frac {2K}{-3\left( \sqrt {2}\right) ^{2} } \\[ 5pt ] &=&-\frac {K}{3} \\[ 5pt ] \end{eqnarray}
\] となるので，実軸との交点は\(\displaystyle \left( -\frac {K}{3}，\mathrm {j}0 \right) \)となる。

(3)ナイキストの安定判別法を適用して，制御系を安定にするゲイン\(K\)の範囲
ワンポイント解説「1.ナイキストの安定判別法」より，安定条件は，
\[
\begin{eqnarray}
-\frac {K}{3} &＞&-1 \\[ 5pt ] K&＜&3 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)図2のフィードバック制御系の特性方程式
図2のフィードバック制御系の伝達関数\(G (s) \)は，
\[
\begin{eqnarray}
G (s) &=&\frac {\displaystyle \frac {2K}{s\left( s^{2} +3s+2 \right) }}{1+\displaystyle \frac {2K}{s\left( s^{2} +3s+2 \right) }} \\[ 5pt ] &=&\frac {2K}{s^{3} +3s^{2}+2s+2K} \\[ 5pt ] \end{eqnarray}
\] となるので，特性方程式は，
\[
\begin{eqnarray}
s^{3} +3s^{2}+2s+2K &=&0 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)特性方程式のラウス表を示したのち，制御系を安定にするゲイン\(K\)の範囲
ワンポイント解説「2.ラウスの安定判別法」より，ラウス表は下表のようになる。
\[
\begin{array}{c|cc}
& 1列 & 2列 \\
\hline
1行 & 1 & 2 \\
2行 & 3 & 2K \\
3行 & \frac {6-2K}{3} & 0 \\
4行 & 2K & \\
\end{array}
\] よって，安定となる条件は，
\[
\begin{eqnarray}
2K &＞&0 \\[ 5pt ] \frac {6-2K}{3}&＞&0 \\[ 5pt ] \end{eqnarray}
\] となるので，\(0 ＜ K ＜ 3 \)と求められる。

(6)図2のフィードバック制御系が安定限界であるとき，閉ループ伝達関数の三つの極
安定限界であるとき，\(K=3\)であるから，特性方程式を整理すると，
\[
\begin{eqnarray}
s^{3} +3s^{2}+2s+6 &=&0 \\[ 5pt ] s^{2}\left( s +3\right) +2\left( s+3 \right) &=&0 \\[ 5pt ] \left( s+3 \right) \left( s^{2}+2 \right) &=&0 \\[ 5pt ] s&=&-3，±\mathrm {j}\sqrt {2}
\end{eqnarray}
\] と求められる。