《理論》〈電子理論〉[R06:問7]MOSFETのソース接地増幅回路に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，ソース接地増幅回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

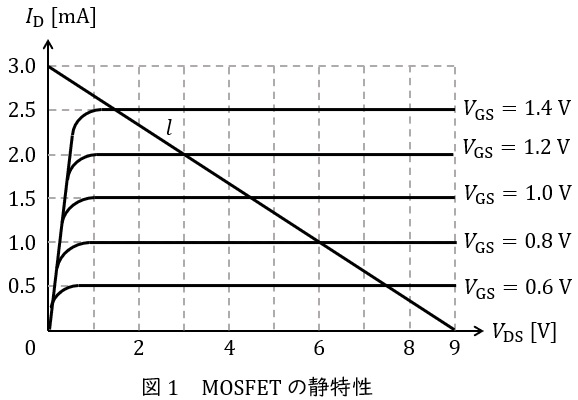
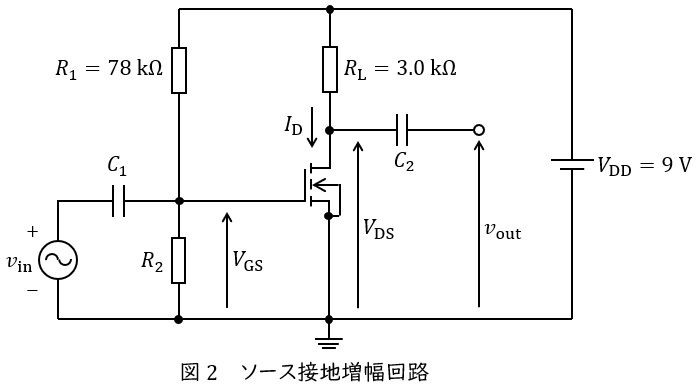
図1の静特性を有する$ \ \mathrm {MOSFET} \ $を用いて図2のソース接地増幅回路を構成する。ただし，$ \ \mathrm {MOSFET} \ $のドレイン電流は飽和領域ではドレイン・ソース間電圧$ \ V_{\mathrm {DS}} \ $に依存しないとする。

まず，入力電圧$ \ v_{\mathrm {in}} \ $を零としたときの回路の各部の直流の電圧及び電流（バイアス電圧及び電流）を考える。$ \ \mathrm {MOSFET} \ $のゲート端子には電流は流れないから，入力電圧$ \ v_{\mathrm {in}} \ $が零のときのゲート・ソース間電圧$ \ V_{\mathrm {GS0}} \ $は電源電圧$ \ V_{\mathrm {DD}} \ $と$ \ R_{\mathrm {1}} \ $と$ \ R_{\mathrm {2}} \ $を用いた文字式で$ \ V_{\mathrm {GS0}}= \ \fbox {　（１）　} \ $と表すことができる。一方，$ \ \mathrm {MOSFET} \ $のドレイン電流$ \ I_{\mathrm {D}} \ $は全て抵抗$ \ R_{\mathrm {L}} \ $を流れるため，$ \ I_{\mathrm {D}} \ $は，$ \ R_{\mathrm {L}} \ $とドレイン・ソース間電圧$ \ V_{\mathrm {DS}} \ $及び$ \ V_{\mathrm {DD}} \ $を用いて$ \ I_{\mathrm {D}}= \ \fbox {　（２）　} \ $と表される。この関係を図2に示す素子値を用いて図1中に描くと直線$ \ l \ $となる。無信号時のドレイン電流$ \ I_{\mathrm {D0}} \ $を$ \ 2 \ \mathrm {mA} \ $とするために必要な$ \ V_{\mathrm {GS0}} \ $の値を図1の直線$ \ l \ $と$ \ \mathrm {MOSFET} \ $の静特性から読み取る。$ \ V_{\mathrm {GS0}} \ $は$ \ \fbox {　（１）　} \ $であるから，この$ \ V_{\mathrm {GS0}} \ $を得るためには$ \ R_{\mathrm {2}} \ $を$ \ \fbox {　（３）　} \ \mathrm {\Omega } \ $とすればよい。

次に$ \ R_{\mathrm {2}} \ $を$ \ \fbox {　（３）　} \ \mathrm {\Omega } \ $とした状態で微小な正弦波電圧$ \ v_{\mathrm {in}} \ $を入力したときの出力電圧を考える。ただし，$ \ v_{\mathrm {in}} \ $の周波数において，各容量のインピーダンスは十分に小さく，短絡と見なせるとする。入力電圧$ \ v_{\mathrm {in}} \ $を加えると$ \ \mathrm {MOSFET} \ $のゲート・ソース間電圧$ \ V_{\mathrm {GS}} \ $は$ \ V_{\mathrm {GS0}} \ $から$ \ V_{\mathrm {GS0}}+\mathit {\Delta }V_{\mathrm {GS}}=V_{\mathrm {GS0}}+v_{\mathrm {in}} \ $に変化する。このときドレイン電流$ \ I_{\mathrm {D}} \ $は$ \ I_{\mathrm {D0}}+\mathit {\Delta }I_{\mathrm {D}} \ $に変化するとする。$ \ \mathit {\Delta }I_{\mathrm {D}} \ $は$ \ \mathrm {MOSFET} \ $のトランスコンダクタンスを$ \ g_{\mathrm {m}} \ $とすると，$ \ \mathit {\Delta }I_{\mathrm {D}}=g_{\mathrm {m}}v_{\mathrm {in}} \ $と近似できるが，$ \ \mathrm {MOSFET} \ $の動作点付近のトランスコンダクタンス$ \ \displaystyle g_{\mathrm {m}}=\frac {\mathit {\Delta }I_{\mathrm {D}}}{\mathit {\Delta }V_{\mathrm {GS}}} \ $は，図1より$ \ g_{\mathrm {m}}= \ \fbox {　（４）　} \ \mathrm {S} \ $であることがわかる。一方，$ \ I_{\mathrm {D}} \ $が$ \ I_{\mathrm {D0}}+\mathit {\Delta }I_{\mathrm {D}} \ $に増加したときの$ \ V_{\mathrm {DS}} \ $の変化量$ \ \mathit {\Delta }V_{\mathrm {DS}} \ $は$ \ \mathit {\Delta }I_{\mathrm {D}} \ $を用いて$ \ \fbox {　（５）　} \ $と表せる。$ \ \mathit {\Delta }V_{\mathrm {DS}} \ $は$ \ v_{\mathrm {out}} \ $と等しいことから図2のソース接地増幅回路の電圧増幅度は$ \ \displaystyle \frac {v_{\mathrm {out}}}{v_{\mathrm {in}}}=\frac {\mathit {\Delta }V_{\mathrm {DS}}}{\mathit {\Delta }V_{\mathrm {GS}}}= \ \fbox {　（６）　} \ $倍と求められる。

〔問7の解答群〕
\[
\begin{eqnarray}
&（イ）&　-7.5　　　　　&（ロ）&　2.5　　　　　&（ハ）&　7.5 \\[ 5pt ] &（ニ）&　0.5 \ \mathrm {m}　　　　　&（ホ）&　2.5 \ \mathrm {m}　　　　　&（ヘ）&　0.4 \ \mathrm {k} \\[ 5pt ] &（ト）&　1.2 \ \mathrm {k}　　　　　&（チ）&　12 \ \mathrm {k}　　　　　&（リ）&　24 \ \mathrm {k} \\[ 5pt ] &（ヌ）&　V_{\mathrm {DD}}-R_{1}\mathit {\Delta }I_{\mathrm {D}}　　　　　&（ル）&　R_{\mathrm {L}}\mathit {\Delta }I_{\mathrm {D}}　　　　　　&（ヲ）&　-R_{\mathrm {L}}\mathit {\Delta }I_{\mathrm {D}} \\[ 5pt ] &（ワ）&　\frac {R_{\mathrm {L}}}{V_{\mathrm {DD}}-V_{\mathrm {DS}}}　　　　　&（カ）&　\frac {V_{\mathrm {DD}}-V_{\mathrm {DS}}}{R_{\mathrm {L}}}　　　　　　&（ヨ）&　V_{\mathrm {DD}}-\frac {V_{\mathrm {DS}}}{R_{\mathrm {L}}} \\[ 5pt ] &（タ）&　\frac {V_{\mathrm {DD}}}{R_{\mathrm {1}}+R_{\mathrm {2}}}　　　　　&（レ）&　\frac {R_{\mathrm {1}}}{R_{\mathrm {1}}+R_{\mathrm {2}}}V_{\mathrm {DD}}　　　　　　&（ソ）&　\frac {R_{\mathrm {2}}}{R_{\mathrm {1}}+R_{\mathrm {2}}}V_{\mathrm {DD}} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

$ \ \mathrm {MOSFET} \ $のソース接地増幅回路の静特性を考える問題です。
本問は電気回路の基本公式以外に特段特別な公式は必要ありませんが，解法を理解している必要があります。解法パターンもかなり決まっているので，ぜひ本問でマスターするようにして下さい。

【解答】

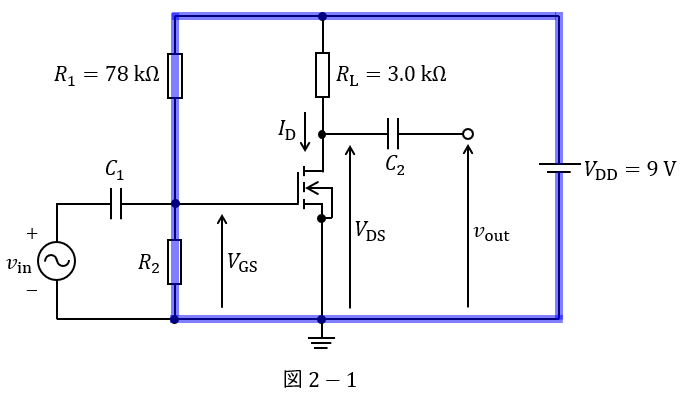
(1)解答：ソ
図2-1に示す閉回路に分圧の法則を適用すると，
\[
\begin{eqnarray}
V_{\mathrm {GS0}} &=&\frac {R_{\mathrm {2}}}{R_{\mathrm {1}}+R_{\mathrm {2}}}V_{\mathrm {DD}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

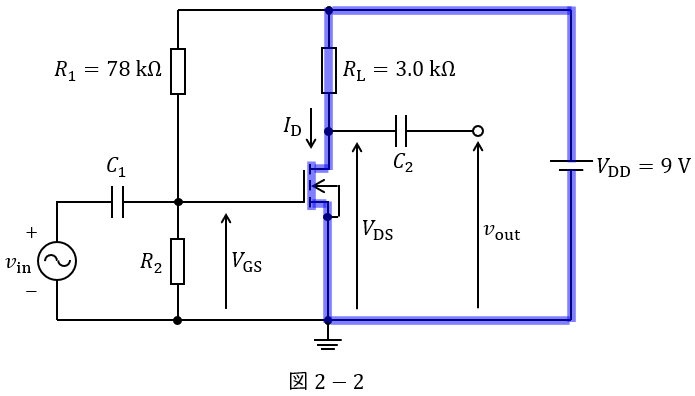
(2)解答：カ
図2-2に示す閉回路にキルヒホッフの法則の電圧則を適用すると，
\[
\begin{eqnarray}
V_{\mathrm {DD}} &=&R_{\mathrm {L}}I_{\mathrm {D}}+V_{\mathrm {DS}} \\[ 5pt ] R_{\mathrm {L}}I_{\mathrm {D}}&=&V_{\mathrm {DD}}-V_{\mathrm {DS}} \\[ 5pt ] I_{\mathrm {D}}&=&\frac {V_{\mathrm {DD}}-V_{\mathrm {DS}}}{R_{\mathrm {L}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：チ
図1-1に示すように，無信号時のドレイン電流$ \ I_{\mathrm {D0}}=2 \ \mathrm {[mA]} \ $とするためには，$ \ V_{\mathrm {GS0}}=1.2 \ \mathrm {[V]} \ $とする必要があるため，これを(1)解答式に代入して$ \ R_{2} \ \mathrm {[k\Omega ]} \ $を求めると，
\[
\begin{eqnarray}
1.2 &=&\frac {R_{\mathrm {2}}}{78 \ 000+R_{\mathrm {2}}}\times 9 \\[ 5pt ] 93 \ 600 +1.2R_{\mathrm {2}}&=&9R_{\mathrm {2}} \\[ 5pt ] 7.8R_{\mathrm {2}}&=&93 \ 600 \\[ 5pt ] R_{\mathrm {2}}&=&12 \ 000 \ \mathrm {[\Omega ]}　→　12 \ \mathrm {[k\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。

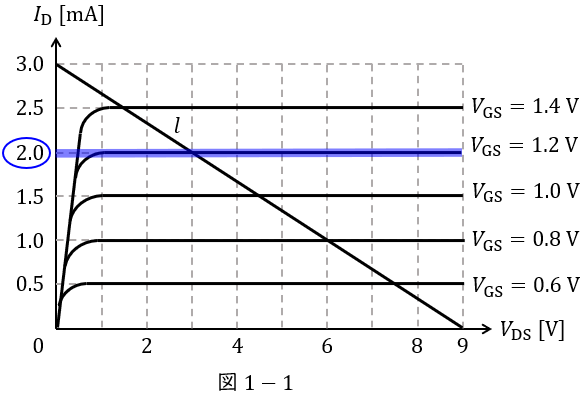
(4)解答：ホ
図1の静特性のグラフを読み取ると，$ \ V_{\mathrm {GS}} \ $が$ \ 0.2 \ \mathrm {V} \ $変化する間に$ \ I_{\mathrm {D}} \ $が$ \ 0.5 \ \mathrm {mA} \ $変化しているから，$ \ \displaystyle g_{\mathrm {m}}=\frac {\mathit {\Delta }I_{\mathrm {D}}}{\mathit {\Delta }V_{\mathrm {GS}}} \ $は，
\[
\begin{eqnarray}
g_{\mathrm {m}}&=&\frac {0.5\times 10^{-3}}{0.2} \\[ 5pt ] &=&2.5\times 10^{-3} \ \mathrm {[S]}　→　2.5 \ \mathrm {[mS]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヲ
(2)解答式を整理すると，
\[
\begin{eqnarray}
I_{\mathrm {D}}&=&\frac {V_{\mathrm {DD}}-V_{\mathrm {DS}}}{R_{\mathrm {L}}} \\[ 5pt ] R_{\mathrm {L}}I_{\mathrm {D}}&=&V_{\mathrm {DD}}-V_{\mathrm {DS}} \\[ 5pt ] V_{\mathrm {DS}}&=&-R_{\mathrm {L}}I_{\mathrm {D}}+V_{\mathrm {DD}} \\[ 5pt ] \end{eqnarray}
\] となるので，変化量$ \ \mathit {\Delta }V_{\mathrm {DS}} \ $は，
\[
\begin{eqnarray}
\mathit {\Delta }V_{\mathrm {DS}}&=&-R_{\mathrm {L}}\mathit {\Delta }I_{\mathrm {D}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(6)解答：イ
(4)解答式より，
\[
\begin{eqnarray}
g_{\mathrm {m}}&=&\frac {\mathit {\Delta }I_{\mathrm {D}}}{\mathit {\Delta }V_{\mathrm {GS}}} \\[ 5pt ] \mathit {\Delta }V_{\mathrm {GS}}&=&\frac {\mathit {\Delta }I_{\mathrm {D}}}{g_{\mathrm {m}}} \\[ 5pt ] \end{eqnarray}
\] となり，これと(5)解答式より，電圧増幅度$ \ \displaystyle \frac {v_{\mathrm {out}}}{v_{\mathrm {in}}}=\frac {\mathit {\Delta }V_{\mathrm {DS}}}{\mathit {\Delta }V_{\mathrm {GS}}} \ $は，
\[
\begin{eqnarray}
\frac {v_{\mathrm {out}}}{v_{\mathrm {in}}}&=&\frac {\mathit {\Delta }V_{\mathrm {DS}}}{\mathit {\Delta }V_{\mathrm {GS}}} \\[ 5pt ] &=&\frac {-R_{\mathrm {L}}\mathit {\Delta }I_{\mathrm {D}}}{\displaystyle \frac {\mathit {\Delta }I_{\mathrm {D}}}{g_{\mathrm {m}}}} \\[ 5pt ] &=&-g_{\mathrm {m}}R_{\mathrm {L}} \\[ 5pt ] &=&-2.5\times 10^{-3}\times 3.0\times 10^{3} \\[ 5pt ] &=&-7.5 \\[ 5pt ] \end{eqnarray}
\] と求められる。