【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,直流回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまるものを解答群の中から選びなさい。
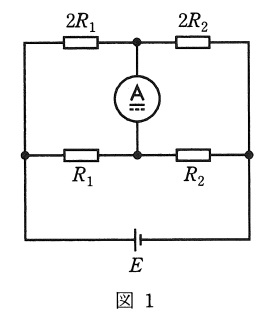
図1に示す平衡条件を満たすブリッジ回路において,抵抗\( \ R_{2} \ \)に抵抗\( \ 3R_{2} \ \)を直列又は並列に接続したときに,電流計に流れる電流を補償定理を使って求めてみよう。ただし,\( \ E \ \)は直流電圧源の大きさであり,電圧源と電流計の内部抵抗は無視できるものとする。
図1では電流計には電流は流れていない。したがって,題意の電流を求めるとき,\( \ 3R_{2} \ \)を接続したことによる変化分を考えればよい。
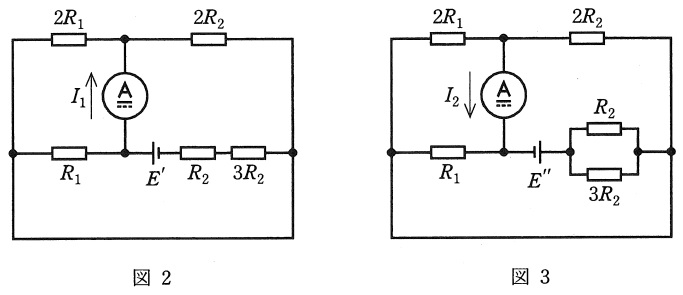
補償定理によれば,\( \ 3R_{2} \ \)を直列に接続したことによる電流の変化分は,図2に示す回路で計算できる。\( \ R_{2} \ \)と\( \ 3R_{2} \ \)に接続される電圧源の大きさ\( \ E^{\prime } \ \)は\( \ \fbox { (1) } \ \)となるから,電流計に流れる電流\( \ I_{1} \ \)は\( \ \fbox { (2) } \ \)となる。
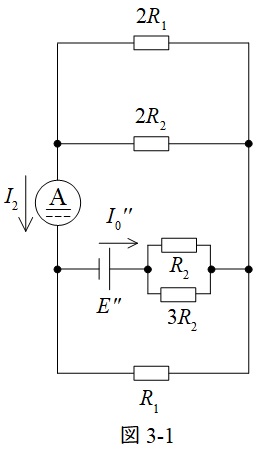
同様に,\( \ R_{2} \ \)と並列に\( \ 3R_{2} \ \)を接続したときに電流計に流れる電流\( \ I_{2} \ \)は,図3に示す回路で計算できる。\( \ R_{2} \ \)に\( \ 3R_{2} \ \)を並列に接続したことによる\( \ R_{2} \ \)に対する抵抗の変化分の絶対値は\( \ \fbox { (3) } \ \)となる。したがって,電圧源の大きさ\( \ E^{\prime \prime} \ \)は\( \ \fbox { (4) } \ \)となり,\( \ I_{2} \ \)は\( \ \fbox { (5) } \ \)となる。
〔問2の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {E}{11R_{1}+9R_{2}} &(ロ)& \frac {E}{16R_{1}+12R_{2}} &(ハ)& \frac {E}{R_{1}+2R_{2}} \\[ 5pt ]
&(ニ)& \frac {3R_{2}}{R_{1}+4R_{2}}E &(ホ)& \frac {E}{2R_{1}+4R_{2}} &(ヘ)& \frac {E}{8R_{1}+6R_{2}} \\[ 5pt ]
&(ト)& \frac {R_{2}E}{2R_{1}+4R_{2}} &(チ)& \frac {R_{2}}{4} &(リ)& \frac {3}{4}E \\[ 5pt ]
&(ヌ)& \frac {3R_{2}}{R_{1}+R_{2}}E &(ル)& 2R_{2} &(ヲ)& \frac {3R_{2}}{4} \\[ 5pt ]
&(ワ)& \frac {R_{2}E}{11R_{1}+9R_{2}} &(カ)& \frac {2R_{2}E}{R_{1}+R_{2}} &(ヨ)& \frac {R_{2}E}{4\left( R_{1}+R_{2}\right) }
\end{eqnarray}
\]
【ワンポイント解説】
補償定理を扱う問題です。途中の回路計算は電流値を求める計算がやや複雑になるため,限られた試験時間の中では本問(2),(5)は後回しにし,時間があれば解いた方が良いと思います。
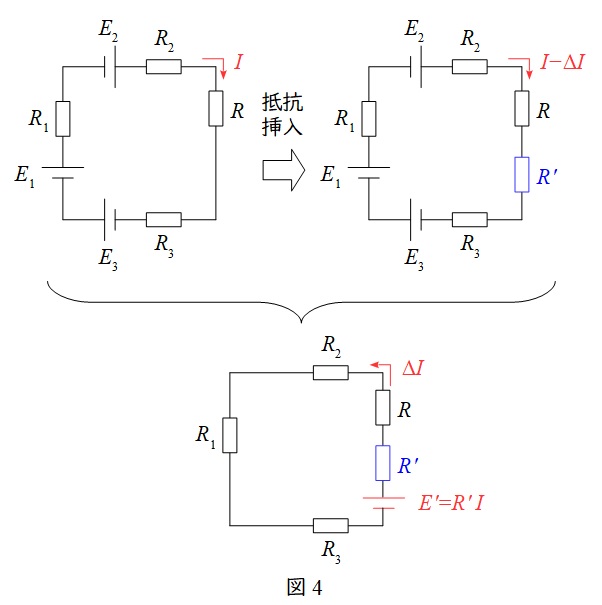
1.補償定理
図4のように,ある回路があり,一つの抵抗\( \ R \ \)に電流\( \ I \ \)が流れているとき,\( \ R \ \)に直列に\( \ R^{\prime } \ \)を接続したときの各箇所の電流変化は,他の電源を取り除き,\( \ R^{\prime } \ \)と直列に\( \ E^{\prime }=R^{\prime }I \ \)の起電力を反対方向に挿入したときに流れる電流の大きさ\( \ \Delta I \ \)に等しいという定理です。
図4のような単純な回路であればイメージがしやすいと思います。
【関連する「電気の神髄」記事】
【解答】
(1)解答:ヌ
図1の\( \ R_{2} \ \)に流れる電流\( \ I_{0} \ \)は,電流計に流れる電流は0であるから,
\[
\begin{eqnarray}
I_{0}&=&\frac {E}{R_{1}+R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,補償定理より,図2の補償起電力\( \ E^{\prime } \ \)は抵抗増加分\( \ 3R_{2} \ \)と\( \ I_{0} \ \)の積と等しいから,
\[
\begin{eqnarray}
E^{\prime }&=&3R_{2}I_{0} \\[ 5pt ]
&=&3R_{2}\cdot \frac {E}{R_{1}+R_{2}} \\[ 5pt ]
&=&\frac {3R_{2}}{R_{1}+R_{2}}E
\end{eqnarray}
\]
と求められる。
(2)解答:ホ
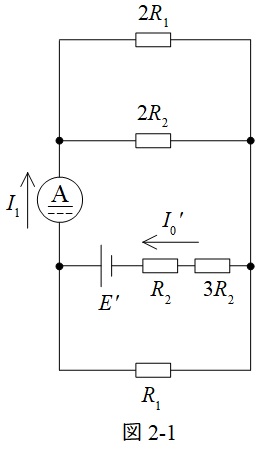
図2は図2-1のように整理し,書き換えることができる。
図2-1の合成抵抗\( \ R \ \)は,
\[
\begin{eqnarray}
R&=&R_{2}+3R_{2}+\frac {1}{\displaystyle \frac {1}{R_{1}}+\frac {1}{2R_{1}}+\frac {1}{2R_{2}}} \\[ 5pt ]
&=&4R_{2}+\frac {1}{\displaystyle \frac {3}{2R_{1}}+\frac {1}{2R_{2}}} \\[ 5pt ]
&=&4R_{2}+\frac {2R_{1}R_{2}}{\displaystyle R_{1}+3R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
であるから,電源\( \ E^{\prime } \ \)を流れる電流\( \ I_{0}^{\prime } \ \)は,
\[
\begin{eqnarray}
I_{0}^{\prime }&=&\frac {E^{\prime }}{R} \\[ 5pt ]
&=&\frac{\displaystyle \frac {3R_{2}}{R_{1}+R_{2}}E}{\displaystyle 4R_{2}+\frac {2R_{1}R_{2}}{\displaystyle R_{1}+3R_{2}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められ、さらに電流計を流れる電流\( \ I_{1} \ \)は,
\[
\begin{eqnarray}
I_{1}&=&\frac {R_{1}}{\displaystyle R_{1}+\frac {1}{\displaystyle \frac {1}{2R_{1}}+\frac {1}{2R_{2}}}}I_{0}^{\prime } \\[ 5pt ]
&=&\frac {R_{1}}{\displaystyle R_{1}+\frac {2R_{1}R_{2}}{R_{1}+R_{2}}}\cdot \frac{\displaystyle \frac {3R_{2}}{R_{1}+R_{2}}E}{\displaystyle 4R_{2}+\frac {2R_{1}R_{2}}{\displaystyle R_{1}+3R_{2}}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {3R_{1}R_{2}}{R_{1}+R_{2}}E}{\displaystyle \left( R_{1}+\frac {2R_{1}R_{2}}{R_{1}+R_{2}}\right) \left( 4R_{2}+\frac {2R_{1}R_{2}}{R_{1}+3R_{2}}\right)} \\[ 5pt ]
\end{eqnarray}
\]
となるので,分母分子を\( \ R_{1}R_{2} \ \)で割って整理すると
\[
\begin{eqnarray}
I_{1}&=&\frac {3E}{ \displaystyle \left(R_{1}+R_{2}\right)\left( 1+\frac {2R_{2}}{R_{1}+R_{2}}\right) \left( 4+\frac {2R_{1}}{R_{1}+3R_{2}}\right)} \\[ 5pt ]
&=&\frac {3E}{ \displaystyle \left(R_{1}+R_{2}+2R_{2}\right) \left( 4+\frac {2R_{1}}{R_{1}+3R_{2}}\right)} \\[ 5pt ]
&=&\frac {3E}{ \displaystyle \left(R_{1}+3R_{2}\right) \left( 4+\frac {2R_{1}}{R_{1}+3R_{2}}\right)} \\[ 5pt ]
&=&\frac {3E}{ \displaystyle 4\left( R_{1}+3R_{2}\right) +2R_{1}} \\[ 5pt ]
&=&\frac {3E}{6R_{1}+12R_{2}} \\[ 5pt ]
&=&\frac {E}{2R_{1}+4R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:チ
\( \ R_{2} \ \)と\( \ 3R_{2} \ \)の並列合成抵抗は,
\[
\begin{eqnarray}
\frac {R_{2}\cdot 3R_{2}}{R_{2}+3R_{2}}&=&\frac {3}{4}R_{2} \\[ 5pt ]
\end{eqnarray}
\]
であるから,変化分の絶対値は,
\[
\begin{eqnarray}
R_{2}-\frac {3}{4}R_{2}&=&\frac {R_{2}}{4} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヨ
補償定理より,図3の補償起電力\( \ E^{\prime \prime } \ \)は抵抗変化分\( \ \displaystyle \frac {R_{2}}{4} \ \)と\( \ I_{0} \ \)の積と等しいから,
\[
\begin{eqnarray}
E^{\prime \prime }&=&\frac {R_{2}}{4}I_{0} \\[ 5pt ]
&=&\frac {R_{2}}{4}\cdot \frac {E}{R_{1}+R_{2}} \\[ 5pt ]
&=&\frac {R_{2}E}{4\left(R_{1}+R_{2}\right)} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:イ
(2)と同様に電流計を流れる電流\( \ I_{2} \ \)は,
\[
\begin{eqnarray}
I_{2}&=&\frac {\displaystyle \frac {R_{1}R_{2}E}{4\left(R_{1}+R_{2}\right)}}{\displaystyle \left( R_{1}+\frac {2R_{1}R_{2}}{R_{1}+R_{2}}\right) \left(\frac{3}{4}R_{2}+\frac {2R_{1}R_{2}}{R_{1}+3R_{2}}\right)} \\[ 5pt ]
\end{eqnarray}
\]
となるので,分母分子を\( \ R_{1}R_{2} \ \)で割って整理すると
\[
\begin{eqnarray}
I_{2}&=&\frac {E}{\displaystyle 4\left(R_{1}+R_{2}\right)\left( 1+\frac {2R_{2}}{R_{1}+R_{2}}\right) \left(\frac{3}{4}+\frac {2R_{1}}{R_{1}+3R_{2}}\right)} \\[ 5pt ]
&=&\frac {E}{\displaystyle \left\{ \left(R_{1}+R_{2}\right)+2R_{2}\right\} \left(3+\frac {8R_{1}}{R_{1}+3R_{2}}\right)} \\[ 5pt ]
&=&\frac {E}{\displaystyle \left(R_{1}+3R_{2}\right) \left(3+\frac {8R_{1}}{R_{1}+3R_{2}}\right)} \\[ 5pt ]
&=&\frac {E}{\displaystyle 3\left(R_{1}+3R_{2}\right) +8R_{1}} \\[ 5pt ]
&=&\frac {E}{11R_{1}+9R_{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん