《理論》〈電気回路〉[H27:問5] 三相交流回路に関する計算問題

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，三相交流回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。ただし，$ \ a \ $は複素数で$ \ \displaystyle a=e^{\mathrm {j}\frac {2}{3}\pi} \ $とする。

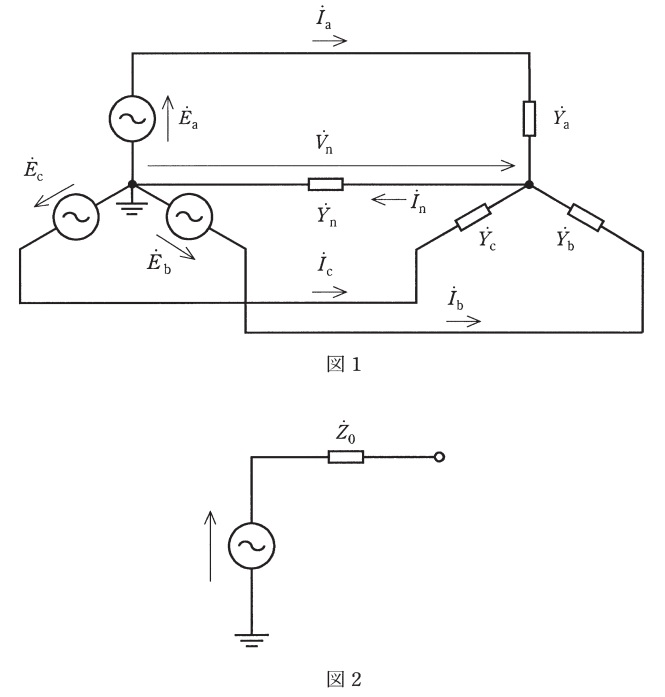
図1に示すように，対称三相交流電圧源にアドミタンスが$ \ {\dot Y}_{\mathrm {a}} \ $，$ \ {\dot Y}_{\mathrm {b}} \ $，$ \ {\dot Y}_{\mathrm {c}} \ $の$ \ \mathrm {Y} \ $形不平衡負荷を接続した。負荷と電源の中性点を結ぶ中性線のアドミタンスを$ \ {\dot Y}_{\mathrm {n}} \ $とする。$ \ {\dot E}_{\mathrm {a}}=100 \ \mathrm {V}∠0° \ $であり，相回転は$ \ {\dot E}_{\mathrm {a}} \ $，$ \ {\dot E}_{\mathrm {b}} \ $，$ \ {\dot E}_{\mathrm {c}} \ $の順($ \ {\dot E}_{\mathrm {b}}=a^{2}{\dot E}_{\mathrm {a}} \ $，$ \ {\dot E}_{\mathrm {c}}=a{\dot E}_{\mathrm {a}} \ $)とする。$ \ \mathrm {Y} \ $形不平衡負荷のアドミタンス$ \ {\dot Y}_{\mathrm {a}} \ $，$ \ {\dot Y}_{\mathrm {b}} \ $，$ \ {\dot Y}_{\mathrm {c}} \ $は以下の形とする。
\[
\left(
\begin{array}{c}
{\dot Y}_{\mathrm {a}} \\
{\dot Y}_{\mathrm {b}} \\
{\dot Y}_{\mathrm {c}}
\end{array}
\right)
=
\left(
\begin{array}{c}
{\dot Y}_{\mathrm {0}}+\Delta \dot Y \\
{\dot Y}_{\mathrm {0}}+a\Delta \dot Y \\
{\dot Y}_{\mathrm {0}}+a^{2}\Delta \dot Y
\end{array}
\right)
，　\Delta \dot Y ≠ 0　・・・・・・・　①
\] ここで，$ \ 1+a+a^{2}=0 \ $，$ \ a^{3}=1 \ $に注意する。

ミルマンの定理と①式を使うと，$ \ \mathrm {Y} \ $形負荷の中性点電位$ \ {\dot V}_{\mathrm {n}} \ $と中性線電流$ \ {\dot I}_{\mathrm {n}} \ $の式は，
\[
{\dot V}_{\mathrm {n}}= \ \fbox {　（１）　}，　{\dot I}_{\mathrm {n}}= \ \fbox {　（１）　}\times {\dot Y}_{\mathrm {n}}　・・・・・・・・　②
\] となる。

図1の三相回路の中性点間を短絡又は開放したところ，以下の結果を得た。

(a)　中性点間を短絡すると($ \ {\dot Y}_{\mathrm {n}}=\infty \ $)，中性点電流は$ \ {\dot I}_{\mathrm {n}}=30a \ \mathrm {[A]} \ $となった。

(b)　中性点間を開放すると($ \ {\dot Y}_{\mathrm {n}}=0 \ $)，$ \ \mathrm {Y} \ $形負荷の中性点電位は$ \ {\dot V}_{\mathrm {n}}=100a \ \mathrm {[V]} \ $となった。

②式に(a)と(b)の結果を適用すると，$ \ ({\dot Y}_{0}，\Delta \dot Y)= \ \fbox {　（２）　} \ \mathrm {[S]} \ $となる。

図1の回路を$ \ {\dot Y}_{\mathrm {n}} \ $から見た等価回路を図2のように表すと，(a)及び(b)から$ \ {\dot Z}_{0}= \ \fbox {　（３）　} \ \Omega \ $となる。したがって，図1の回路の中性線で消費する電力が最大となるのは$ \ {\dot Y}_{\mathrm {n}}= \ \fbox {　（４）　} \ \mathrm {S} \ $のときである。そのとき，中性線で消費する電力は$ \ \fbox {　（５）　} \ \mathrm {W} \ $である。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　300　　　　　&（ロ）&　\frac {10a}{3}　　　　　&（ハ）&　\frac {3a}{10} \\[ 5pt ] &（ニ）&　\frac {3{\dot E}_{\mathrm {a}}\Delta \dot Y}{{\dot Y}_{\mathrm {0}}+3{\dot Y}_{\mathrm {n}}}　　　　　&（ホ）&　\left( \frac {1}{10}，\frac {a}{10}\right)　　　　　&（ヘ）&　250 \\[ 5pt ] &（ト）&　\left( \frac {1}{10}，\frac {1}{10}\right) 　　　　　&（チ）&　\left( \frac {1}{10}，\frac {a^{2}}{10}\right) 　　　　　&（リ）&　\frac {10}{3} \\[ 5pt ] &（ヌ）&　750　　　　　&（ル）&　\frac {3a^{2}}{10}　　　　　&（ヲ）&　\frac {3{\dot E}_{\mathrm {a}}\Delta \dot Y}{3{\dot Y}_{\mathrm {0}}+{\dot Y}_{\mathrm {n}}} \\[ 5pt ] &（ワ）&　\frac {3}{10}　　　　　&（カ）&　\frac {10a^{2}}{3}　　　　　&（ヨ）&　\frac {3{\dot E}_{\mathrm {a}}{\dot Y}_{\mathrm {n}}}{3{\dot Y}_{\mathrm {0}}+\Delta \dot Y}
\end{eqnarray}
\]

【ワンポイント解説】

キルヒホッフの法則を用いても解くことは可能ですが，ミルマンの定理を理解していれば，幾分計算が楽になります。一種平成27年度理論問3の$ \ E_{0} \ $の導出もミルマンの定理を用いて解くことが可能なので，本問が終わったら解いてみて下さい。

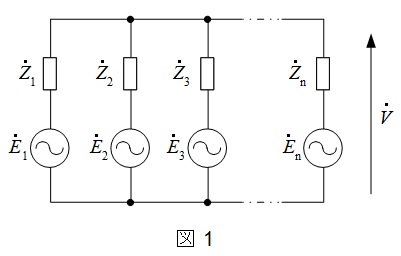
1.ミルマンの定理
図1に示すような並列回路があった時，電圧$ \ \dot V \ $は，
\[
\dot V=\frac {\displaystyle \frac {{\dot E}_{1}}{{\dot Z}_{1}} +\frac {{\dot E}_{2}}{{\dot Z}_{2}}+ \cdots +\frac {{\dot E}_{\mathrm {n}}}{{\dot Z}_{\mathrm {n}}}}{\displaystyle \frac {1}{{\dot Z}_{1}} +\frac {1}{{\dot Z}_{2}}+ \cdots +\frac {1}{{\dot Z}_{\mathrm {n}}}}
\] で求められます。

【関連する「電気の神髄」記事】

　　ミルマンの定理の導出

【解答】

(1)解答：ヲ
ワンポイント解説「1.ミルマンの定理」より中性点電位$ \ {\dot V}_{\mathrm {n}} \ $は，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {n}}&=&\frac {{\dot E}_{\mathrm {a}}{\dot Y}_{\mathrm {a}}+{\dot E}_{\mathrm {b}}{\dot Y}_{\mathrm {b}}+{\dot E}_{\mathrm {c}}{\dot Y}_{\mathrm {c}}}{{\dot Y}_{\mathrm {a}}+{\dot Y}_{\mathrm {b}}+{\dot Y}_{\mathrm {c}}+{\dot Y}_{\mathrm {n}}} \\[ 5pt ] \end{eqnarray}
\] となるので，$ \ {\dot E}_{\mathrm {b}}=a^{2}{\dot E}_{\mathrm {a}} \ $，$ \ {\dot E}_{\mathrm {c}}=a{\dot E}_{\mathrm {a}} \ $及び①を代入すると，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {n}}&=&\frac {{\dot E}_{\mathrm {a}}({\dot Y}_{\mathrm {0}}+\Delta \dot Y)+a^{2}{\dot E}_{\mathrm {a}}({\dot Y}_{\mathrm {0}}+a\Delta \dot Y)+a{\dot E}_{\mathrm {a}}({\dot Y}_{\mathrm {0}}+a^{2}\Delta \dot Y)}{{\dot Y}_{\mathrm {0}}+\Delta \dot Y+{\dot Y}_{\mathrm {0}}+a\Delta \dot Y+{\dot Y}_{\mathrm {0}}+a^{2}\Delta \dot Y+{\dot Y}_{\mathrm {n}}} \\[ 5pt ] &=&\frac {\left( 1+a^{2}+a\right) {\dot E}_{\mathrm {a}}{\dot Y}_{\mathrm {0}}+3{\dot E}_{\mathrm {a}}\Delta \dot Y}{3{\dot Y}_{\mathrm {0}}+\left( 1+a^{2}+a\right) \Delta \dot Y+{\dot Y}_{\mathrm {n}}} \\[ 5pt ] &=&\frac {3{\dot E}_{\mathrm {a}}\Delta \dot Y}{3{\dot Y}_{\mathrm {0}}+{\dot Y}_{\mathrm {n}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。また，中性点電流$ \ {\dot I}_{\mathrm {n}} \ $は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {n}}&=&{\dot V}_{\mathrm {n}}{\dot Y}_{\mathrm {n}} \\[ 5pt ] &=&\frac {3{\dot E}_{\mathrm {a}}\Delta \dot Y}{3{\dot Y}_{\mathrm {0}}+{\dot Y}_{\mathrm {n}}}\times {\dot Y}_{\mathrm {n}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ホ
問題文(a)より，
\[
\begin{eqnarray}
\displaystyle \lim_{ {\dot Y}_{\mathrm {n}} \to \infty } {\dot I}_{\mathrm {n}}&=&30a \\[ 5pt ] \displaystyle \lim_{ {\dot Y}_{\mathrm {n}} \to \infty } \left( \frac {3{\dot E}_{\mathrm {a}}\Delta \dot Y}{3{\dot Y}_{\mathrm {0}}+{\dot Y}_{\mathrm {n}}}\times {\dot Y}_{\mathrm {n}}\right) &=&30a \\[ 5pt ] \displaystyle \lim_{ {\dot Y}_{\mathrm {n}} \to \infty } \left( \frac {3{\dot E}_{\mathrm {a}}\Delta \dot Y}{\frac {3{\dot Y}_{\mathrm {0}}}{{\dot Y}_{\mathrm {n}}}+1}\right) &=&30a \\[ 5pt ] 3{\dot E}_{\mathrm {a}}\Delta \dot Y&=&30a \\[ 5pt ] 3\times 100\Delta \dot Y&=&30a \\[ 5pt ] \Delta \dot Y&=&\frac {a}{10} \\[ 5pt ] \end{eqnarray}
\] と求められる。また，(b)より，
\[
\begin{eqnarray}
\displaystyle \lim_{ {\dot Y}_{\mathrm {n}} \to 0 } {\dot V}_{\mathrm {n}}&=&100a \\[ 5pt ] \displaystyle \lim_{ {\dot Y}_{\mathrm {n}} \to 0 } \left( \frac {3{\dot E}_{\mathrm {a}}\Delta \dot Y}{3{\dot Y}_{\mathrm {0}}+{\dot Y}_{\mathrm {n}}}\right) &=&100a \\[ 5pt ] \frac {{\dot E}_{\mathrm {a}}\Delta \dot Y}{{\dot Y}_{\mathrm {0}}}&=&100a \\[ 5pt ] \frac {\displaystyle 100\cdot \frac {a}{10}}{{\dot Y}_{\mathrm {0}}}&=&100a \\[ 5pt ] {\dot Y}_{\mathrm {0}}&=&\frac {1}{10} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：リ
$ \ z_{0} \ $は図1の回路を$ \ {\dot Y}_{\mathrm {n}} \ $から見た時のインピーダンスであるから，
\[
\begin{eqnarray}
z_{0}&=&\frac {1}{{\dot Y}_{\mathrm {a}}+{\dot Y}_{\mathrm {b}}+{\dot Y}_{\mathrm {c}}} \\[ 5pt ] &=&\frac {1}{3{\dot Y}_{0}} \\[ 5pt ] &=&\frac {10}{3} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ワ
中性線で消費する電力が最大となるのは，$ \ \displaystyle {\dot Y}_{\mathrm {n}}=\frac {1}{z_{0}} \ $の時であるから，
\[
\begin{eqnarray}
{\dot Y}_{\mathrm {n}}&=&\frac {1}{z_{0}} \\[ 5pt ] &=&\frac {3}{10} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヌ
中性線で消費する電力$ \ P_{\mathrm {n}} \ $は，
\[
\begin{eqnarray}
P_{\mathrm {n}}&=&\left| {\dot V}_{\mathrm {n}}^{2}{\dot Y}_{\mathrm {n}}\right| \\[ 5pt ] &=&\left| \left( 50a\right) ^{2}\times \frac {3}{10}\right| \\[ 5pt ] &=&\left| 750a^{2} \right| \\[ 5pt ] &=&750 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] と求められる。