【問題】
【難易度】★★★☆☆(普通)
次の文章は,架空送電線の電気的定数に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
架空送電線では,可とう性などの理由から,一般により線が用いられるが,この場合,素線の実長は中心導体に比べて若干長くなるので,その分抵抗が大きくなる。この割合を\( \ \fbox { (1) } \ \)といい,通常は\( \ 2 \ \mathrm {%} \ \)程度である。また,電線に交流が流れると電流は断面全体にわたって一様に流れず,\( \ \fbox { (2) } \ \)多く流れる。電流の流れる部分の深さ\( \ \delta \ \mathrm {[m]} \ \)は,角周波数を\( \ \omega \ \mathrm {[rad / s]} \ \),透磁率を\( \ \mu \ \mathrm {[H / m]} \ \),導電率を\( \ \sigma \ \mathrm {[S / m]} \ \)として,\( \ \fbox { (3) } \ \mathrm {[m]} \ \)と表される。
正三角形配置された対称三相架空送電線において,電線\( \ 1 \ \)条(単導体)の単位長当たりの作用インダクタンス\( \ L \ \mathrm {[mH / km]} \ \)は,比透磁率を\( \ \mu _{\mathrm {r}} \ \),線間距離を\( \ D \ \mathrm {[m]} \ \),電線半径を\( \ r \ \mathrm {[m]} \ \)として,\( \ \displaystyle L=0.05 \mu _{\mathrm {r}}+0.460 \ 5\log _{10}\frac {D}{r} \ \mathrm {[mH / km]} \ \)と表され,単導体の場合,\( \ \fbox { (4) } \ \mathrm {mH / km} \ \)程度である。また,電線\( \ 1 \ \)条(単導体)の単位長当たりの作用静電容量\( \ C \ \mathrm {[\mu F / km]} \ \)は,比誘電率を\( \ \varepsilon _{\mathrm {r}} \ \),線間距離を\( \ D \ \mathrm {[m]} \ \),電線半径を\( \ r \ \mathrm {[m]} \ \)として,\( \ \fbox { (5) } \ \mathrm {[\mu F / km]} \ \)と表され,単導体の場合,\( \ 0.008~0.01 \ \mathrm {\mu F / km} \ \)程度である。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& C=\frac {0.024 \ 13\varepsilon _{\mathrm {r}}}{\displaystyle \log _{10}\left( \frac {D}{r}\right) } &(ロ)& 中心に近づくほど &(ハ)& C=\frac {\displaystyle \log _{10}\left( \frac {D}{r}\right) }{0.024 \ 13\varepsilon _{\mathrm {r}}} \\[ 5pt ]
&(ニ)& アスペクト比 &(ホ)& \delta =\sqrt {\frac {\omega \mu \sigma }{2}} &(ヘ)& より線と中心導体の接点で \\[ 5pt ]
&(ト)& より込率 &(チ)& \delta =\sqrt {\frac {2\sigma }{\omega \mu }} &(リ)& C=\frac {0.024 \ 13\varepsilon _{\mathrm {r}}}{\displaystyle \log _{10}\left( \frac {r}{D}\right) } \\[ 5pt ]
&(ヌ)& 10 &(ル)& \delta =\sqrt {\frac {2}{\omega \mu \sigma }} &(ヲ)& 1 \\[ 5pt ]
&(ワ)& 0.1 &(カ)& 抵抗率 &(ヨ)& 表面に近くなるほど \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
架空送電線の電気的定数に関する問題です。
架空送電線で覚えておかなければならない定数が出題されていますが,作用インダクタンスと作用静電容量の式を覚えておくのは少し厳しいので,選択肢の中から正答を選択できるレベルで良いかと思います。
1.表皮効果
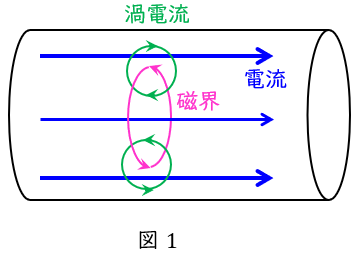
交流電流において,導体内を流れる電流によりアンペールの法則に沿った磁界が発生し,その発生した磁界の変化によりファラデーの電磁誘導の法則に沿った渦電流が発生することで,導体内の電流分布が外側に集中する現象です。
電線の断面積が大きい電線では無視できなくなり,角周波数と透磁率,導電率が大きくなるほど顕著となります。
表皮効果の現れにくさの指標となる電流の流れる部分の深さ\( \ \delta \ \mathrm {[m]} \ \)は,角周波数\( \ \omega \ \mathrm {[rad / s]} \ \),透磁率\( \ \mu \ \mathrm {[H / m]} \ \),導電率\( \ \sigma \ \mathrm {[S / m]} \ \)とすると,
\[
\begin{eqnarray}
\delta &=&\sqrt {\frac {2}{\omega \mu \sigma }} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.送電線の線路定数
架空送電線路の線路定数は,電線の太さ,長さ,配置,種類等の影響を受け,距離が短ければ線路定数も十分小さくなるので無視することができますが,距離が長くなるとその影響を無視できなくなります。
①線路抵抗
電線の抵抗率を\( \ \rho \ \mathrm {[\Omega \cdot {mm}^{2} / m ]} \ \),電線の長さを\( \ l \ \mathrm {[m]} \ \),断面積を\( \ S \ \mathrm {[{mm}^{2}]} \ \)とすると,線路抵抗\( \ R \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
R &=&\frac {\rho l}{S} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
②作用インダクタンス
線間距離\( \ D \ \mathrm {[m]} \ \),電線半径\( \ r \ \mathrm {[m]} \ \)の送電線の作用インダクタンス\( \ L \ \mathrm {[mH/km]} \ \)は,
\[
\begin{eqnarray}
L &=&0.05+0.4605 \log_{10}\frac {D}{r} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。したがって,線間距離\( \ D \ \)と電線半径\( \ r \ \)の比\( \ D/r \ \)が大きくなると作用インダクタンス\( \ L \ \)も大きくなります。
架空送電線でのインダクタンスは\( \ 1.0 \ \mathrm {mH / km} \ \)程度となります。
③作用静電容量
線間距離\( \ D \ \mathrm {[m]} \ \),電線半径\( \ r \ \mathrm {[m]} \ \)の送電線の作用静電容量\( \ C \ \mathrm {[\mu F/km]} \ \)は,
\[
\begin{eqnarray}
C &=&\frac {0.02413}{\displaystyle \log_{10}\frac {D}{r}} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。したがって,線間距離\( \ D \ \)と電線半径\( \ r \ \)の比\( \ D/r \ \)が大きくなると作用静電容量\( \ C \ \)は小さくなります。
架空送電線の作用静電容量は\( \ 0.008~0.01 \ \mathrm { \mu F/km } \ \)程度となります。
④漏れコンダクタンス
がいし表面を流れる電流やコロナ損をコンダクタンスに換算したものですが,その値は非常に小さいので,一般に無視されます。
【解答】
(1)解答:ト
題意より解答候補は,(ニ)アスペクト比,(ト)より込率,(カ)抵抗率,になると思います。
より線とするために,素線の実長が中心導体に比べて若干長くなる割合をより込率といいます。アスペクト比は縦横比のことで,テレビ画面等で使用される比となります。
(2)解答:ヨ
題意より解答候補は,(ロ)中心に近づくほど,(ヘ)より線と中心導体の接点で,(ヨ)表面に近くなるほど,になると思います。
ワンポイント解説「1.表皮効果」の通り,電線に交流が流れると電流は断面全体にわたって一様に流れず,表面に近くなるほど多く流れます。
(3)解答:ル
題意より解答候補は,(ホ)\( \ \displaystyle \delta =\sqrt {\frac {\omega \mu \sigma }{2}} \ \),(チ)\( \ \displaystyle \delta =\sqrt {\frac {2\sigma }{\omega \mu }} \ \),(ル)\( \ \displaystyle \delta =\sqrt {\frac {2}{\omega \mu \sigma }} \ \),になると思います。
ワンポイント解説「1.表皮効果」の通り,電流の流れる部分の深さ\( \ \delta \ \mathrm {[m]} \ \)は\( \ \displaystyle \delta =\sqrt {\frac {2}{\omega \mu \sigma }} \ \)となります。
(4)解答:ヲ
題意より解答候補は,(ヌ)\( \ 10 \ \),(ヲ)\( \ 1 \ \),(ワ)\( \ 0.1 \ \),になると思います。
ワンポイント解説「2.送電線の線路定数」の通り,単導体の場合の作用インダクタンスは\( \ 1 \ \mathrm {mH / km} \ \)程度となります。
(5)解答:イ
題意より解答候補は,(イ)\( \ \displaystyle C=\frac {0.024 \ 13\varepsilon _{\mathrm {r}}}{\displaystyle \log _{10}\left( \frac {D}{r}\right) } \ \),(ハ)\( \ \displaystyle C=\frac {\displaystyle \log _{10}\left( \frac {D}{r}\right) }{0.024 \ 13\varepsilon _{\mathrm {r}}} \ \),(リ)\( \ \displaystyle C=\frac {0.024 \ 13\varepsilon _{\mathrm {r}}}{\displaystyle \log _{10}\left( \frac {r}{D}\right) } \ \),になると思います。
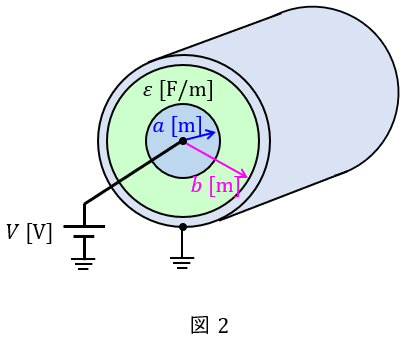
ワンポイント解説「2.送電線の線路定数」の通り,電線\( \ 1 \ \)条(単導体)の単位長当たりの作用静電容量\( \ C \ \mathrm {[\mu F / km]} \ \)は\( \ \displaystyle C=\frac {0.024 \ 13\varepsilon _{\mathrm {r}}}{\displaystyle \log _{10}\left( \frac {D}{r}\right) } \ \)で表されます。図2に示す同心同軸ケーブルの静電容量が\( \ C=\displaystyle \frac {2\pi \varepsilon }{\displaystyle \ln \frac {b}{a}} \ \)であることから理解しておくと正答は幾分導き出しやすくなるかと思います。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん