【問題】
【難易度】★☆☆☆☆(易しい)
各種の電気設備から発生する高調波電流により電圧波形がひずみ,他の電気設備に障害を与える事例が発生している。このような高調波電流を抑制するためには,電圧ひずみと高調波流出電流の管理が必要であり,そのための諸量を適切に把握することが重要である。
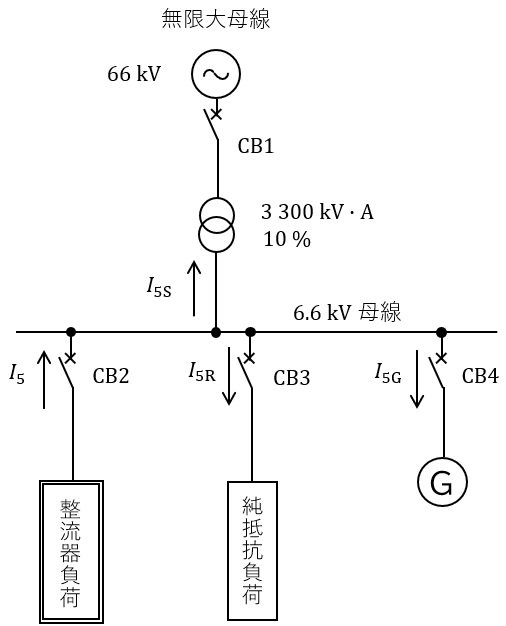
図のように,\( \ 66 \ \mathrm {kV} \ \)系統から受電する\( \ 6.6 \ \mathrm {kV} \ \)母線に整流器負荷,純抵抗負荷,発電機が遮断器\( \ \mathrm {CB2} \ \),\( \ \mathrm {CB3} \ \),\( \ \mathrm {CB4} \ \)を介して接続されている。\( \ \mathrm {CB1} \ \)は,受電用遮断器である。受電変圧器の容量は\( \ 3 \ 300 \ \mathrm {kV\cdot A} \ \),インピーダンスは自己容量基準で\( \ 10 \ \mathrm {%} \ \)であり,抵抗分と励磁インピーダンスとを無視できるものとする。整流器負荷は\( \ 5 \ \)次高調波電流を発生し,その他の高調波成分は無視できるものとする。
(1) 高調波が電気設備に与える可能性のある障害を二つ挙げよ。
(2) \( \ 5 \ \)次高調波に対する受電変圧器の\( \ 2 \ \)次側換算リアクタンス\( \ \mathrm {[\Omega ]} \ \)を求めよ。
(3) \( \ \mathrm {CB1} \ \)と\( \ \mathrm {CB2} \ \)のみが閉であるとする。整流器負荷が発生する\( \ 5 \ \)次高調波電流の大きさが\( \ I_{5} \ \mathrm {[A]} \ \)のとき,\( \ 6.6 \ \mathrm {kV} \ \)母線の相電圧に含まれる\( \ 5 \ \)次高調波成分の大きさを求めよ。
(4) 上記(3)の状態で\( \ \mathrm {CB3} \ \)が閉となったとする。系統に流れ出す\( \ 5 \ \)次高調波電流の大きさ\( \ I_{\mathrm {5S}} \ \)を純抵抗負荷の値\( \ R \ \mathrm {[\Omega ]} \ \)と\( \ I_{\mathrm {5}} \ \)とで表せ。
(5) \( \ \mathrm {CB1} \ \)が開で,発電機が整流器負荷と純抵抗負荷とに電源供給している。このときの\( \ 6.6 \ \mathrm {kV} \ \)母線相電圧に含まれる\( \ 5 \ \)次高調波成分の大きさを求めよ。ただし,発電機の\( \ 5 \ \)次高調波に対するリアクタンスを\( \ X_{5} \ \mathrm {[\Omega ]} \ \)とする。
【ワンポイント解説】
電気設備から発生する高調波電流の系統への影響を考える問題です。
\( \ 3 \ \)種の頃から出題範囲とされ,計算もそれほど難解ではないため,ほとんどの受験生が選択し高得点を得た問題であると思います。
ぜひこういう問題を確実に得点し,合格を勝ち取るようにして下さい。
1.高調波
高調波は標準周波数の\( \ 2 \ \)倍,\( \ 3 \ \)倍,\( \ \cdots \ \)の周波数の波形を持つ波のことで,「高圧又は特別高圧で受電する需要家の高調波抑制対策ガイドライン」では高調波環境目標レベルとして\( \ 6.6 \ \mathrm {kV} \ \)配電系統で\( \ 5 \ \mathrm {%} \ \),特別高圧系統で\( \ 3 \ \mathrm {%} \ \)を維持すると定められています。
①高調波の発生源
アーク炉等の負荷,変圧器の磁気飽和,パワーエレクトロニクス機器等。
\( \ 3 \ \)次,\( \ 5 \ \)次,\( \ 7 \ \)次,\( \ 11 \ \)次の奇数次の高調波が多く,偶数次では\( \ 2 \ \)次の高調波も発生します。\( \ 3 \ \)次の高調波は変圧器の\( \ \Delta \ \)結線で還流させることができるので,電力系統としては最も多い\( \ 5 \ \)次の高調波に対する対策を行います。
②高調波による影響
・コンデンサやリアクトルが過熱,焼損
・電力用ヒューズのエレメントが過熱,溶断
・変圧器が振動,過熱
・発電機の巻線が過熱
・保護継電器が誤動作
・配電用遮断器が誤トリップ
・ラジオやテレビに可聴雑音が発生
・半導体機器が故障及び性能劣化
③高調波の対策
・整流器の相数を増加する
・電力用コンデンサには必ず直列リアクトルを設置する
・パッシブフィルタ,アクティブフィルタを設置する
・短絡容量の大きな系統から受電する
2.第\( \ n \ \)次高調波のリアクタンス
リアクトルとコンデンサの基本波リアクタンス\( \ X_{\mathrm {L}} \ \mathrm {[\Omega ]} \ \)及び\( \ X_{\mathrm {C}} \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
X_{\mathrm {L}}&=&\omega L \\[ 5pt ]
&=&2\pi f L \\[ 5pt ]
X_{\mathrm {C}}&=&\frac {1}{\omega C} \\[ 5pt ]
&=&\frac {1}{2\pi f C} \\[ 5pt ]
\end{eqnarray}
\]
となりますが,第\( \ n \ \)調波に対するリアクタンス\( \ X_{\mathrm {L5}} \ \mathrm {[\Omega ]} \ \)及び\( \ X_{\mathrm {C5}} \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
X_{\mathrm {L5}}&=&2\pi \cdot nf L \\[ 5pt ]
&=&n\cdot 2\pi f L \\[ 5pt ]
&=&nX_{\mathrm {L}} \\[ 5pt ]
X_{\mathrm {C5}}&=&\frac {1}{2\pi \cdot nf C} \\[ 5pt ]
&=&\frac {1}{n\cdot 2\pi f C} \\[ 5pt ]
&=&\frac {X_{\mathrm {C}}}{n} \\[ 5pt ]
\end{eqnarray}
\]
となります。すなわち,リアクトルは\( \ n \ \)倍,コンデンサは\( \ \displaystyle \frac {1}{n} \ \)倍となります。
3.オーム法からパーセントインピーダンス法への変換
基準容量を\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \),基準電圧を\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \),基準電流を\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)とすると,
\[
\begin{eqnarray}
%Z&=&\frac {ZI_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}\times 100 (定義) \\[ 5pt ]
&=&\frac {\sqrt {3}ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ]
&=&\frac {\sqrt {3}ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ]
&=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100 (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)高調波が電気設備に与える可能性のある障害を二つ
(ポイント)
・ワンポイント解説「1.高調波」の通りです。
(試験センター解答)
・力率改善用コンデンサに過熱や振動・騒音が発生する。焼損に至ることもある。
・トランスの損失(鉄損と銅損)が増大する。
・電動機の回転が周期的に変動する。振動・騒音が発生し,損失が増大する。
・電力量計に計測誤差が発生する。
・保護継電器に誤動作,誤不動作が発生する。
(2)\( \ 5 \ \)次高調波に対する受電変圧器の\( \ 2 \ \)次側換算リアクタンス\( \ \mathrm {[\Omega ]} \ \)
基準容量\( \ P_{\mathrm {n}}=3 \ 300 \ \mathrm {[kV\cdot A]} \ \),基準電圧\( \ V_{\mathrm {n}}=6.6 \ \mathrm {[kV]} \ \)なので,受電変圧器\( \ %X_{\mathrm {T}}=10 \ \mathrm {[%]} \ \)の\( \ 2 \ \)次側換算リアクタンス\( \ X_{\mathrm {T}} \ \mathrm {[\Omega ]} \ \)は,ワンポイント解説「3.オーム法からパーセントインピーダンス法への変換」の通り,
\[
\begin{eqnarray}
%X_{\mathrm {T}}&=&\frac {P_{\mathrm {n}}X_{\mathrm {T}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ]
X_{\mathrm {T}}&=&\frac {%X_{\mathrm {T}}V_{\mathrm {n}}^{2}}{100P_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {10\times \left( 6.6\times 10^{3}\right) ^{2}}{100\times 3 \ 300\times 10^{3}} \\[ 5pt ]
&=&1.32 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,\( \ 5 \ \)次高調波に対する受電変圧器の\( \ 2 \ \)次側換算リアクタンス\( \ X_{\mathrm {T5}} \ \mathrm {[\Omega ]} \ \)は,ワンポイント解説「2.第\( \ n \ \)調波に対するリアクタンス」の通り,
\[
\begin{eqnarray}
X_{\mathrm {T5}}&=&5X_{\mathrm {T}} \\[ 5pt ]
&=&5\times 1.32 \\[ 5pt ]
&=&6.6 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ \mathrm {CB1} \ \)と\( \ \mathrm {CB2} \ \)が閉,整流器負荷が発生する\( \ 5 \ \)次高調波電流の大きさが\( \ I_{5} \ \mathrm {[A]} \ \)のとき,\( \ 6.6 \ \mathrm {kV} \ \)母線の相電圧に含まれる\( \ 5 \ \)次高調波成分の大きさ
\( \ \mathrm {CB1} \ \)と\( \ \mathrm {CB2} \ \)のみが閉であるとき,\( \ I_{5} \ \mathrm {[A]} \ \)は受電変圧器側に全て流れる。
したがって,(2)解答式より,\( \ 6.6 \ \mathrm {kV} \ \)母線の相電圧に含まれる\( \ 5 \ \)次高調波成分の大きさ\( \ V_{5} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {5}}&=&X_{\mathrm {T5}}I_{5} \\[ 5pt ]
&=&6.6I_{5} \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)\( \ \mathrm {CB3} \ \)が閉となったとき,系統に流れ出す\( \ 5 \ \)次高調波電流の大きさ\( \ I_{\mathrm {5S}} \ \)
純抵抗負荷\( \ R \ \mathrm {[\Omega ]} \ \)のインピーダンスは\( \ 5 \ \)次高調波でも同じであるため,分流の法則より,系統に流れ出す\( \ 5 \ \)次高調波電流の大きさ\( \ I_{\mathrm {5S}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {5S}}&=&\left| \frac {R}{R+\mathrm {j}X_{\mathrm {T5}}}\right| I_{5} \\[ 5pt ]
&=& \frac {R}{\sqrt {R^{2}+X_{\mathrm {T5}}^{2}}} I_{5} \\[ 5pt ]
&=& \frac {R}{\sqrt {R^{2}+6.6^{2}}} I_{5} \\[ 5pt ]
&=&\frac {R}{\sqrt {R^{2}+43.56}} I_{5} \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)\( \ \mathrm {CB1} \ \)が開のときの\( \ 6.6 \ \mathrm {kV} \ \)母線相電圧に含まれる\( \ 5 \ \)次高調波成分の大きさ
純抵抗負荷と発電機の\( \ 5 \ \)次高調波に対するインピーダンスの大きさ\( \ Z_{\mathrm {5}} \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
Z_{\mathrm {5}}&=&\left| \frac {R\cdot \mathrm {j}X_{\mathrm {5}}}{R+\mathrm {j}X_{\mathrm {5}}}\right| \\[ 5pt ]
&=&\left| \frac {\mathrm {j}R X_{\mathrm {5}}}{R+\mathrm {j}X_{\mathrm {5}}}\right| \\[ 5pt ]
&=& \frac {R X_{\mathrm {5}}}{\sqrt {R^{2}+X_{\mathrm {5}}^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ 6.6 \ \mathrm {kV} \ \)母線相電圧に含まれる\( \ 5 \ \)次高調波成分の大きさ\( \ V_{5}^{\prime } \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{5}^{\prime }&=&Z_{\mathrm {5}}I_{\mathrm {5}} \\[ 5pt ]
&=& \frac {R X_{\mathrm {5}}}{\sqrt {R^{2}+X_{\mathrm {5}}^{2}}}I_{\mathrm {5}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん