【問題】
【難易度】★★★☆☆(普通)
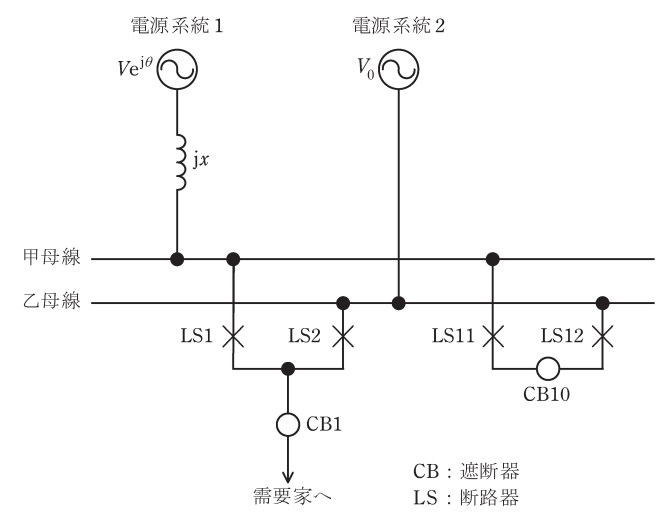
二つの異なる電源系統から受電する電気所が,図のように\( \ \mathrm {CB1} \ \)を介して需要家に電気を供給している。電源系統\( \ 2 \ \)につながる乙母線は無限大母線と考えてよく,線間電圧の大きさは\( \ V_{0} \ \mathrm {[V]} \ \left( V_{0}>0\right) \ \)である。甲母線がつながる電源系統\( \ 1 \ \)には背後インピーダンス\( \ \mathrm {j}x \ \mathrm {[\Omega ]} \ \)があり,背後電源の線間電圧の大きさが\( \ V \ \mathrm {[V]} \ \left( V>0\right) \ \),電源系統\( \ 2 \ \)に対する位相が\( \ \theta \ \mathrm {[rad ]} \ \)進んでいるとする。\( \ \mathrm {CB10} \ \)は母線連絡遮断器であり,常時開で運用されている。乙母線から供給していた需要家を,甲母線からの供給に無停電で切り換える必要が生じた。次の問に答えよ。
(1) 切り換えを手動で行うこととした。操作の手順を順序立てて述べよ。ただし,切り換え前には,\( \ \mathrm {LS11} \ \)及び\( \ \mathrm {LS12} \ \)が共に開放されているとする。
(2) 甲母線の三相短絡電流の大きさ\( \ I_{\mathrm {s}} \ \mathrm {[A]} \ \),短絡容量\( \ S \ \mathrm {[V\cdot A]} \ \)を求めよ。
(3) \( \ \mathrm {CB10} \ \)を投入したときに\( \ \mathrm {LS11} \ \)から\( \ \mathrm {LS12} \ \)に向けて流れる電流\( \ \dot I \ \mathrm {[A]} \ \)を求めよ。ただし,投入の前後で\( \ V_{0} \ \),\( \ V \ \),\( \ \theta \ \)の値に変化はないものとし,需要家への供給電流は無視できるものとする。
(4) 電源系統\( \ 1 \ \)の電圧の大きさ\( \ V \ \)が電源系統\( \ 2 \ \)の電圧の大きさ\( \ V_{0} \ \)と等しいとする。この場合,母線電圧の位相差\( \ \theta \ \)が小さいならば,\( \ \mathrm {CB10} \ \)を投入したときに\( \ \mathrm {CB10} \ \)を流れる電流の大きさが\( \ I_{\mathrm {s}}\cdot \left| \theta \right| \ \mathrm {[A]} \ \)で近似できることを示せ。
【ワンポイント解説】
(1)は母線切替に関する問題,(2)からは短絡電流の計算となります。計算量が比較的少なく,時間的にはだいぶゆとりを持って解ける問題ですが,内容をきちんと理解していないと全問間違いとなってしまいます。
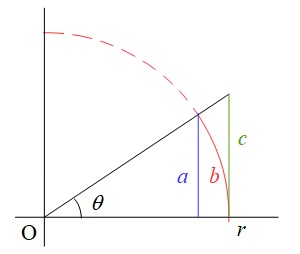
1.\( \ \theta \ \)が十分に小さい時の\( \ \sin \theta \ \)の近似式
下図において,\( \ a < b < c \ \)であるので,ここから,以下の式変形により\( \ \sin \theta \ \)の近似式を導き出します。
\[
\begin{eqnarray}
a &<& b < c \\[ 5pt ]
\frac {a}{r} &<& \frac {b}{r} < \frac {c}{r} \\[ 5pt ]
\sin \theta &<& \frac {r\theta }{r} < \tan \theta \\[ 5pt ]
\sin \theta &<& \theta < \frac {\sin \theta }{\cos \theta } \\[ 5pt ]
1 &<& \frac {\theta}{\sin \theta } < \frac {1}{\cos \theta } \\[ 5pt ]
1 &>& \frac {\sin \theta }{\theta} > \cos \theta \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \theta \ \)が十分に小さい時,\( \ \cos \theta ≃1 \ \)なので,\( \ \displaystyle \frac {\sin \theta }{\theta}≃1 \ \)となります。したがって,
\[
\begin{eqnarray}
\frac {\sin \theta }{\theta}&≃&1 \\[ 5pt ]
\sin \theta &≃&\theta \\[ 5pt ]
\end{eqnarray}
\]
と近似できます。
※ 試験対策では,この結果を暗記しておけば大丈夫です。
【解答】
(1)切り換えを手動で行う時の操作の手順
(ポイント)
・無停電であること,電圧の投入及び遮断を必ず遮断器(\( \ \mathrm {CB} \ \))で行うという理屈を理解していれば順序も自ずと出てくると思います。
(試験センター解答例)
①両母線電圧の同期を検定し,電圧の大きさの差,位相差が小さいことを確認する。(同期検定①を CB10 投入の直前としても可とする)
②LS11 を投入する。(LS12 を投入でも可とする)
③LS12 を投入する。(②を LS12 とした場合,LS11 を投入する)
④CB10 を投入する。
⑤LS1 を投入する。
⑥LS2 を開放する。
⑦CB10 を開放する。
⑧LS11 を開放する。(LS12 を開放でも可とする)
⑨LS12 を開放する。(⑧を LS12 とした場合,LS11 を開放する)
(2)甲母線の三相短絡電流の大きさ\( \ I_{\mathrm {s}} \ \mathrm {[A]} \ \),短絡容量\( \ S \ \mathrm {[V\cdot A]} \ \)
甲母線に繋がっている背後インピーダンスは\( \ \mathrm {j}x \ \)のみなので,三相短絡電流\( \ I_{\mathrm {s}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {s}} &=&\frac {V}{\sqrt {3}x} \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となり,短絡容量\( \ S \ \)は,
\[
\begin{eqnarray}
S &=&\sqrt {3}VI_{\mathrm {s}} \\[ 5pt ]
&=&\frac {V^{2}}{x} \ \mathrm {[V\cdot A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ \mathrm {CB10} \ \)を投入したときに\( \ \mathrm {LS11} \ \)から\( \ \mathrm {LS12} \ \)に向けて流れる電流\( \ \dot I \ \mathrm {[A]} \ \)
\( \ {\dot V}_{0} \ \)を基準とすると,
\[
\begin{eqnarray}
{\dot V}_{0}&=&V_{0} \\[ 5pt ]
\dot V&=&V\left( \cos \theta +\mathrm {j}\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
\dot I&=&\frac {\dot V-{\dot V}_{0}}{\mathrm {j}\sqrt {3}x} \\[ 5pt ]
&=&\frac {V\left( \cos \theta +\mathrm {j}\sin \theta \right) -V_{0}}{\mathrm {j}\sqrt {3}x} \\[ 5pt ]
&=&\frac {V\sin \theta }{\sqrt {3}x}+\mathrm {j}\frac {V_{0}-V\cos \theta }{\sqrt {3}x} \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)\( \ \mathrm {CB10} \ \)を投入したときに\( \ \mathrm {CB10} \ \)を流れる電流の大きさが\( \ I_{\mathrm {s}}\cdot \left| \theta \right| \ \mathrm {[A]} \ \)で近似できることを示す
(3)の解答式において,\( \ V≃V_{0} \ \)とすると,
\[
\begin{eqnarray}
\dot I&=&\frac {V_{0}\sin \theta }{\sqrt {3}x}+\mathrm {j}\frac {V_{0}\left( 1-\cos \theta \right) }{\sqrt {3}x} \\[ 5pt ]
\end{eqnarray}
\]
となり,ワンポイント解説「1.\( \ \theta \ \)が十分に小さい時の\( \ \sin \theta \ \)の近似式」の通り\( \ \sin \theta ≃ \theta \ \),\( \ \cos \theta ≃ 1 \ \)とすると,
\[
\begin{eqnarray}
\dot I&≃&\frac {V_{0}\theta }{\sqrt {3}x}+\mathrm {j}\frac {V_{0}\left( 1-1 \right) }{\sqrt {3}x} \\[ 5pt ]
&=&\frac {V_{0}\theta }{\sqrt {3}x} \\[ 5pt ]
\end{eqnarray}
\]
となり,これと(2)より,
\[
\begin{eqnarray}
\left| \dot I\right| &=&I_{\mathrm {s}}\cdot \left| \theta \right| \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん