【問題】
【難易度】★☆☆☆☆(易しい)
滑り\( \ s \ \)で運転している三相誘導電動機の星形換算一相分の等価回路を下図に示す。ただし,励磁回路および一次抵抗は無視できるものとし,二次抵抗は周波数により変化しないものとする。
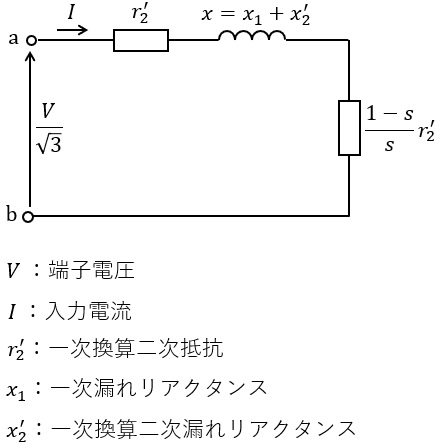
以下の問に答えよ。ただし,(1)~(4)については,記号\( \ \left( s,V,r_{2}^{\prime },x \right) \ \)及び同期角速度\( \ \omega _{\mathrm {s}} \ \)の中から必要な記号を用いて答えよ。
(1) 入力電流\( \ I \ \)及び機械的出力\( \ P_{\mathrm {o}} \ \)の式をそれぞれ示せ。
(2) 発生トルク\( \ T \ \)の式を示せ。
(3) 始動トルク\( \ T_{\mathrm {s}} \ \)の式を示せ。
(4) 最大トルク\( \ T_{\mathrm {m}} \ \)の式を示せ。
(5) この誘導電動機の最大トルク\( \ T_{\mathrm {m}} \ \)は始動トルク\( \ T_{\mathrm {s}} \ \)の\( \ 2 \ \)倍であった。\( \ T_{\mathrm {m}} \ \)となるときの滑り\( \ s_{\mathrm {m}} \ \)の値を求めよ。
【ワンポイント解説】
三相誘導電動機のトルク,始動トルク,最大トルクを検討する問題です。
平成29年機械制御問1に類題が出題され,かつ平成29年よりも計算量が少なかったため,多くの受験生が選択し正答した問題であるかと思います。
(1)及び(2)において,試験センター解答に合わせ\( \ r_{2}^{\prime } \ \)を分母に持ってきていますが,分子のままでも誤りでなければ問題ないかと思います。誘導機は過去問と似たパターンの出題も多いので,多くの過去問に取り組み,問題慣れするようにして下さい。
1.誘導機の滑り\( \ s \ \)
誘導機の同期速度が\( \ N_{\mathrm {s}} \ \mathrm {[{min} ^{-1}]} \ \),回転速度が\( \ N \ \mathrm {[{min} ^{-1}]} \ \)である時,誘導機の滑り\( \ s \ \)は,
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
と定義されるので,\( \ N \ \)について整理すると,
\[
\begin{eqnarray}
s N_{\mathrm {s}}&=&N_{\mathrm {s}}-N \\[ 5pt ]
N&=&\left( 1-s\right) N_{\mathrm {s}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係
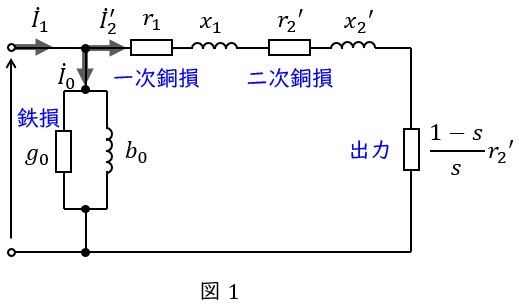
誘導電動機の\( \ \mathrm {L} \ \)形等価回路は図1のようになります。図1において,\( \ {\dot V}_{1} \ \mathrm {[V]} \ \)は一次側端子電圧,\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は一次電流,\( \ {\dot I}_{2}^{\prime } \ \mathrm {[A]} \ \)は二次電流の一次換算,\( \ {\dot I}_{0} \ \mathrm {[A]} \ \)は励磁電流,\( \ r_{1} \ \mathrm {[\Omega ]} \ \)は一次巻線抵抗,\( \ r_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次巻線抵抗の一次換算,\( \ x_{1} \ \mathrm {[\Omega ]} \ \)は一次漏れリアクタンス,\( \ x_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次漏れリアクタンスの一次換算,\( \ s \ \)は滑りとなります。
図1より,出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \),二次銅損\( \ P_{\mathrm {c2}} \ \mathrm {[W]} \ \),二次入力\( \ P_{2} \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {o}} &=& 3\frac {1-s}{s}r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ]
P_{\mathrm {c2}} &=& 3r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ]
P_{2} &=& P_{\mathrm {o}}+P_{\mathrm {c2}} =3\frac {r_{2}^{\prime }}{s}{I_{2}^{\prime }}^{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,誘導電動機の二次入力\( \ P_{2} \ \mathrm {[W]} \ \),出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \),二次銅損\( \ P_{\mathrm {c2}} \ \mathrm {[W]} \ \)には,
\[
\begin{eqnarray}
P_{2}:P_{\mathrm {o}}:P_{\mathrm {c2}} &=& 1:(1-s):s \\[ 5pt ]
\end{eqnarray}
\]
の関係があることが分かります。
3.誘導電動機のトルク
図1より,三相誘導電動機のトルク\( \ T \ \)は,
\[
\begin{eqnarray}
T &=&\frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ]
&=&\frac {P_{\mathrm {2}}\left( 1-s\right) }{\omega _{\mathrm {s}}\left( 1-s\right) } \\[ 5pt ]
&=&\frac {P_{\mathrm {2}}}{\omega _{\mathrm {s}}} \\[ 5pt ]
&=& \frac {1}{\omega _{\mathrm {s}}}\frac {3V_{1}^{2}\displaystyle \frac {r_{2}^{\prime }}{s}}{\left( r_{1}+\displaystyle \frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
(1)入力電流\( \ I \ \)及び機械的出力\( \ P_{\mathrm {o}} \ \)
\( \ \displaystyle r_{2}^{\prime }+\frac {1-s}{s}r_{2}^{\prime }=\frac {r_{2}^{\prime }}{s} \ \)であることから,問題図にキルヒホッフの法則を適用すると,入力電流\( \ I \ \)は,
\[
\begin{eqnarray}
I &=&\frac {\displaystyle \frac {V}{\sqrt {3}}}{\displaystyle \sqrt {\left( \frac {r_{2}^{\prime }}{s}\right) ^{2}+x^{2}}} \\[ 5pt ]
&=&\frac {V}{\displaystyle \sqrt {3}\sqrt {\left( \frac {r_{2}^{\prime }}{s}\right) ^{2}+x^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,機械的出力\( \ P_{\mathrm {o}} \ \)は,ワンポイント解説「2.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係」の通り,
\[
\begin{eqnarray}
P_{\mathrm {o}} &=& 3\frac {1-s}{s}r_{2}^{\prime }I^{2} \\[ 5pt ]
&=& 3\frac {1-s}{s}r_{2}^{\prime }\left\{ \frac {V}{\displaystyle \sqrt {3}\sqrt {\left( \frac {r_{2}^{\prime }}{s}\right) ^{2}+x^{2}}}\right\} ^{2} \\[ 5pt ]
&=& \frac {1-s}{s}r_{2}^{\prime } \cdot \frac {V^{2}}{\displaystyle \left( \frac {r_{2}^{\prime }}{s}\right) ^{2}+x^{2}} \\[ 5pt ]
&=& \frac {\left( 1-s\right) r_{2}^{\prime } V^{2}}{\displaystyle s\left\{ \left( \frac {r_{2}^{\prime }}{s}\right) ^{2}+x^{2}\right\} } \\[ 5pt ]
&=& \frac {\left( 1-s\right) V^{2}}{\displaystyle \frac {s}{r_{2}^{\prime }}\left\{ \left( \frac {r_{2}^{\prime }}{s}\right) ^{2}+x^{2}\right\} } \\[ 5pt ]
&=& \frac {\left( 1-s\right) V^{2}}{\displaystyle \frac {r_{2}^{\prime }}{s} + \frac {s}{r_{2}^{\prime }}x^{2} } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)発生トルク\( \ T \ \)
(1)解答式より,二次入力\( \ P_{\mathrm {2}} \ \)は,ワンポイント解説「2.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係」の通り,
\[
\begin{eqnarray}
P_{\mathrm {2}} &=& \frac {P_{\mathrm {o}}}{1-s} \\[ 5pt ]
&=& \frac {1}{1-s}\cdot \frac {\left( 1-s\right) V^{2}}{\displaystyle \frac {r_{2}^{\prime }}{s} + \frac {s}{r_{2}^{\prime }}x^{2} } \\[ 5pt ]
&=& \frac {V^{2}}{\displaystyle \frac {r_{2}^{\prime }}{s} + \frac {s}{r_{2}^{\prime }}x^{2} } \\[ 5pt ]
\end{eqnarray}
\]
となるので,トルク\( \ T \ \)は,ワンポイント解説「3.誘導電動機のトルク」の通り,
\[
\begin{eqnarray}
T &=&\frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ]
&=&\frac {P_{\mathrm {2}}\left( 1-s\right) }{\omega _{\mathrm {s}}\left( 1-s\right) } \\[ 5pt ]
&=&\frac {P_{\mathrm {2}}}{\omega _{\mathrm {s}}} \\[ 5pt ]
&=&\frac {V^{2}}{\displaystyle \omega _{\mathrm {s}}\left( \frac {r_{2}^{\prime }}{s} + \frac {s}{r_{2}^{\prime }}x^{2}\right) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)始動トルク\( \ T_{\mathrm {s}} \ \)
始動時の滑りは\( \ s=1 \ \)であるため,始動トルク\( \ T_{\mathrm {s}} \ \)は,(2)解答式に\( \ s=1 \ \)を代入すると,
\[
\begin{eqnarray}
T_{\mathrm {s}} &=&\frac {V^{2}}{\displaystyle \omega _{\mathrm {s}}\left( \frac {r_{2}^{\prime }}{1} + \frac {1}{r_{2}^{\prime }}x^{2}\right) } \\[ 5pt ]
&=&\frac {V^{2}}{\displaystyle \omega _{\mathrm {s}}\left( r_{2}^{\prime } + \frac {x^{2}}{r_{2}^{\prime }}\right) } \\[ 5pt ]
&=&\frac {r_{2}^{\prime }V^{2}}{\displaystyle \omega _{\mathrm {s}}\left( {r_{2}^{\prime }}^{2} + x^{2}\right) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)最大トルク\( \ T_{\mathrm {m}} \ \)
最大トルクとなるのは(2)解答式において分母の値が最小となるときであるから,\( \ \displaystyle A=\frac {r_{2}^{\prime }}{s} + \frac {s}{r_{2}^{\prime }}x^{2} \ \)とおくと,\( \ \displaystyle \frac {\mathrm {d}A}{\mathrm {d}s}=0 \ \)となるとき最大トルクが得られる。よって,そのときの滑り\( \ s_{\mathrm {m}} \ \)は,電動機運転であるため\( \ 0<s_{\mathrm {m}}<1 \ \)であることに注意すると,
\[
\begin{eqnarray}
\frac {\mathrm {d}A}{\mathrm {d}s} =-\frac {r_{2}^{\prime }}{s_{\mathrm {m}}^{2}}+ \frac {1}{r_{2}^{\prime }}x^{2}&=&0 \\[ 5pt ]
\frac {r_{2}^{\prime }}{s_{\mathrm {m}}^{2}}&=&\frac {1}{r_{2}^{\prime }}x^{2} \\[ 5pt ]
\frac {s_{\mathrm {m}}^{2}}{r_{2}^{\prime }}&=&\frac {r_{2}^{\prime }}{x^{2}} \\[ 5pt ]
s_{\mathrm {m}}^{2}&=&\frac {{r_{2}^{\prime }}^{2}}{x^{2}} \\[ 5pt ]
s_{\mathrm {m}}&=&\frac {{r_{2}^{\prime }}}{x} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,このときのトルク\( \ T_{\mathrm {m}} \ \)は,
\[
\begin{eqnarray}
T_{\mathrm {m}} &=&\frac {V^{2}}{\displaystyle \omega _{\mathrm {s}}\left( \frac {r_{2}^{\prime }}{s_{\mathrm {m}}} + \frac {s_{\mathrm {m}}}{r_{2}^{\prime }}x^{2}\right) } \\[ 5pt ]
&=&\frac {V^{2}}{\displaystyle \omega _{\mathrm {s}}\left( \frac {r_{2}^{\prime }}{\displaystyle \frac {{r_{2}^{\prime }}}{x}} + \frac {\displaystyle \frac {{r_{2}^{\prime }}}{x}}{r_{2}^{\prime }}x^{2}\right) } \\[ 5pt ]
&=&\frac {V^{2}}{\displaystyle \omega _{\mathrm {s}}\left( x+x\right) } \\[ 5pt ]
&=&\frac {V^{2}}{\displaystyle 2\omega _{\mathrm {s}}x } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)\( \ T_{\mathrm {m}} \ \)が\( \ T_{\mathrm {s}} \ \)の\( \ 2 \ \)倍であるとき,\( \ T_{\mathrm {m}} \ \)となる滑り\( \ s_{\mathrm {m}} \ \)
(3)及び(4)解答式において,\( \ T_{\mathrm {m}}=2T_{\mathrm {s}} \ \)であるから,
\[
\begin{eqnarray}
\frac {V^{2}}{\displaystyle 2\omega _{\mathrm {s}}x }&=&2\times \frac {r_{2}^{\prime }V^{2}}{\displaystyle \omega _{\mathrm {s}}\left( {r_{2}^{\prime }}^{2} + x^{2}\right) } \\[ 5pt ]
\frac {1}{\displaystyle 2x }&=&\frac {2r_{2}^{\prime }}{\displaystyle {r_{2}^{\prime }}^{2} + x^{2}} \\[ 5pt ]
{r_{2}^{\prime }}^{2} + x^{2}&=&4r_{2}^{\prime }x \\[ 5pt ]
{r_{2}^{\prime }}^{2} -4r_{2}^{\prime }x+ x^{2}&=&0 \\[ 5pt ]
\end{eqnarray}
\]
となり,解の公式を適用すると,
\[
\begin{eqnarray}
r_{2}^{\prime }&=&2x±\sqrt {\left( 2x\right) ^{2}-x^{2}} \\[ 5pt ]
&=&2x±\sqrt {3x^{2}} \\[ 5pt ]
&=&\left( 2±\sqrt {3}\right) x \\[ 5pt ]
\end{eqnarray}
\]
となる。これより,\( \ T_{\mathrm {m}} \ \)となる滑り\( \ s_{\mathrm {m}} \ \)は,(4)より\( \ \displaystyle s_{\mathrm {m}}=\frac {{r_{2}^{\prime }}}{x} \ \)であることから,
\[
\begin{eqnarray}
s_{\mathrm {m}}&=&\frac {{r_{2}^{\prime }}}{x} \\[ 5pt ]
&=&\frac {\left( 2±\sqrt {3}\right) x}{x} \\[ 5pt ]
&=&2±\sqrt {3} \\[ 5pt ]
\end{eqnarray}
\]
となり,電動機運転時\( \ 0<s<1 \ \)であるから,\( \ s_{\mathrm {m}}=2-\sqrt {3} \ \)と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん