【問題】
【難易度】★★★☆☆(普通)
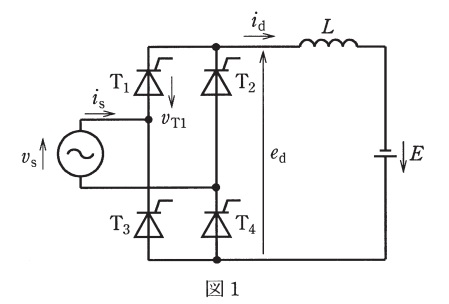
図1に,電池を含む直流回路と電力を授受する,サイリスタを用いた単相整流回路を示す。この回路は,サイリスタの制御角を調整することによって直流電力を交流電力に変換して交流電源に送る動作ができるので,この場合は他励インバータとも呼ばれる。直流リアクトルのインダクタンス\(L\)は電流リプルが無視できるほどに十分大きく,交流電源のインピーダンス,転流重なり角,サイリスタの電圧降下,直流リアクトルの抵抗,電池の内部抵抗などは無視できるものとして,次の問に答えよ。
(1) 交流電源電圧を\(v_{\mathrm {s}}=\sqrt {2}V\sin \omega t\)として,制御角\(\alpha \)で運転しているときの直流電圧\(e_{\mathrm {d}}\)の平均値\(E_{\mathrm {d}}\)を表す式を,\(V\)及び\(\alpha \)を用いて示せ。
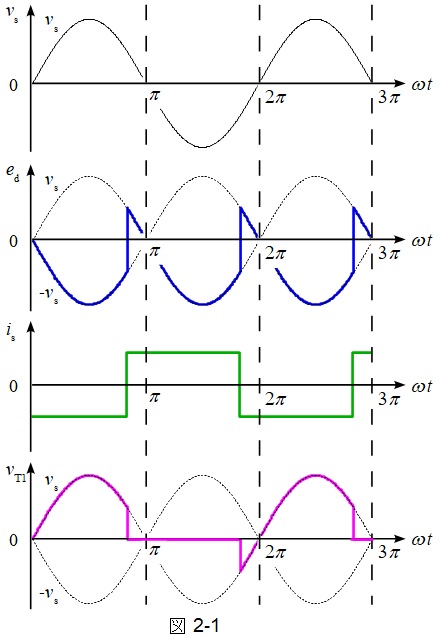
(2) 制御角\(\alpha =150°\)のインバータモードで運転していて,直流電流\(i_{\mathrm {d}}\)は\(i_{\mathrm {d}}=I_{\mathrm {d}}\)一定の定常状態とする。図2が答案用紙に印刷されているので,直流電圧\(e_{\mathrm {d}}\),交流電流\(i_{\mathrm {s}}\),及びサイリスタ\(T_{1}\)に印加される電圧\(v_{\mathrm {T1}}\)の波形を太い線で明確に描け。
(3) 上記(2)において,交流電源の周波数を\(f=50\mathrm {Hz}\)とする。このときのサイリスタの転流余裕角\(\gamma [°]\)はいくらであるか。また,サイリスタをターンオフさせる逆バイアス時間(ホールドオフ期間)\(t_{\mathrm {off} } \ \mathrm {[ms]}\)はいくらになるか。
(4) 上記(2)の定常状態において,交流電源電圧は\(V=200 \ \mathrm {V}\),直流回路には直流電流\(I_{\mathrm {d}}=100 \ \mathrm {A}\)が流れているものとする。交流電源に送る有効電力\(P \ \mathrm {[W]}\)及び交流電流\(i_{\mathrm {s}}\)の基本波実効値\(I_{\mathrm {f}} \ \mathrm {[A]}\)はいくらであるか。
(5) 次に,電池の電圧\(E\)は電流,充電量などに関係なく一定であるとして,上記(4)の状態から交流電源に送る有効電力を2倍に増加させたい。他励インバータの制御角\(\alpha \)を過渡的にどのように変化させ,そしてその後どのような定常状態の値になるように制御すればよいかを説明せよ。

【ワンポイント解説】
単相整流回路の問題で一種のパワーエレクトロニクスの問題としては比較的易しめの問題となっています。時間が少ない時も部分点が狙える問題と言えます。
【解答】
(1)直流電圧\(e_{\mathrm {d}}\)の平均値\(E_{\mathrm {d}}\)を表す式
直流電圧\(e_{\mathrm {d}}\)の平均値\(E_{\mathrm {d}}\)は制御遅れ角\(\alpha \)から\(\pi +\alpha \)までの平均値となるので,
\[
\begin{eqnarray}
E_{\mathrm {d}} &=& \frac {1}{\pi }\int _{\alpha }^{\pi +\alpha }e_{\mathrm {d}} \ \mathrm {d} ( \omega t ) \\[ 5pt ]
&=& \frac {1}{\pi }\int _{\alpha }^{\pi +\alpha }\sqrt {2}V\sin \omega t \ \mathrm {d} ( \omega t ) \\[ 5pt ]
&=& \frac {\sqrt {2}V}{\pi }\left[ -\cos \omega t\right] _{\alpha }^{\pi +\alpha } \\[ 5pt ]
&=& \frac {2\sqrt {2}V}{\pi }\cos \alpha \\[ 5pt ]
&≒& 0.900V\cos \alpha\\[ 5pt ]
\end{eqnarray}
\]
(2)直流電圧\(e_{\mathrm {d}}\),交流電流\(i_{\mathrm {s}}\),及びサイリスタ\(T_{1}\)に印加される電圧\(v_{\mathrm {T1}}\)の波形
図2-1の通りとなる。(\(v_{\mathrm {T1}}\)の向きに注意して下さい。)
(3)サイリスタの転流余裕角\(\gamma [°]\),逆バイアス時間(ホールドオフ期間)\(t_{\mathrm {off} } \ \mathrm {[ms]}\)
制御遅れ角が\(150°\)であるので,
\[
\begin{eqnarray}
\gamma &=& 180-150 \\[ 5pt ]
&=& 30 [°]\\[ 5pt ]
\end{eqnarray}
\]
となり,周波数が\(50 \ \mathrm {Hz}\)であるので,1サイクルあたりの時間\(T\)は,
\[
\begin{eqnarray}
T &=& \frac {1}{50} \\[ 5pt ]
&=& 0.02 \ \mathrm {[s]} → 20 \ \mathrm {[ms]}\\[ 5pt ]
\end{eqnarray}
\]
となるので,逆バイアス時間\(t_{\mathrm {off} } \ \mathrm {[ms]}\)は,
\[
\begin{eqnarray}
t_{\mathrm {off} } &=& T\times \frac {\gamma }{360} \\[ 5pt ]
&=& 20\times \frac {30 }{360} \\[ 5pt ]
&≒& 1.6667 → 1.67 \ \mathrm {[ms]}\\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)交流電源に送る有効電力\(P \ \mathrm {[W]}\)及び交流電流\(i_{\mathrm {s}}\)の基本波実効値\(I_{\mathrm {f}} \ \mathrm {[A]}\)
(1)より直流電圧\(e_{\mathrm {d}}\)の平均値の大きさは,
\[
\begin{eqnarray}
\left| E_{\mathrm {d}}\right| &=& \left| \frac {2\sqrt {2}V}{\pi }\cos \alpha \right| \\[ 5pt ]
&=& \left| \frac {2\sqrt {2}\times 200}{\pi }\cos 150° \right| \\[ 5pt ]
&≒& 155.94 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,有効電力\(P \ \mathrm {[W]}\)は,
\[
\begin{eqnarray}
P &=&\left| E_{\mathrm {d}}\right| I_{\mathrm {d}} \\[ 5pt ]
&=& 155.94\times 100 \\[ 5pt ]
&=& 15594 → 15600 \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
と求められ,これより交流電流\(i_{\mathrm {s}}\)の基本波実効値\(I_{\mathrm {f}} \ \mathrm {[A]}\)は,
\[
\begin{eqnarray}
I_{\mathrm {f}} &=&\left| \frac {P}{V\cos \alpha } \right| \\[ 5pt ]
&=& \left| \frac {15594}{200 \cos 150° } \right| \\[ 5pt ]
&=& \left| \frac {15594}{\displaystyle 200 \times \frac {\sqrt {3}}{2} } \right| \\[ 5pt ]
&≒& 90.032 → 90.0 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)交流電源に送る有効電力を2倍にするため他励インバータの制御角\(\alpha \)を過渡的にどのように変化
有効電力を2倍にするためには電流を2倍にすればよいので,制御角\(\alpha \)を\(\alpha =150°\)から小さくして\(I_{\mathrm {d}} = 200 \ \mathrm {A}\)に近くなるまで上昇させ,その後\(\alpha \)を戻せばよい。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん