【問題】
【難易度】★★☆☆☆(やや易しい)
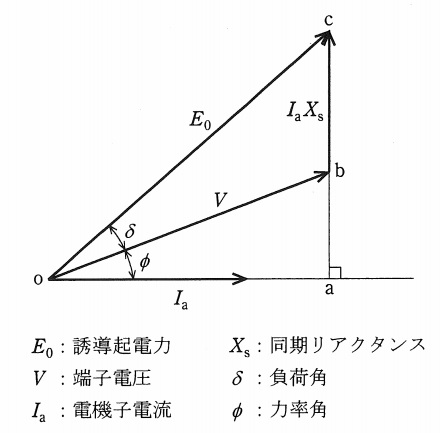
図は,三相星形接続の円筒形同期発電機のベクトル図である。この図を参照して,次の問に答えよ。ただし,図の電圧,電流およびリアクタンスの記号は定格皮相電力基準の単位法で表した大きさを示している。また,電機子抵抗による電圧降下や磁気飽和は無視するものとする。
(1) 電圧変動率\( \ [%] \ \)の算出式を図に記載された記号を用いて示せ。
(2) 図から,\( \ E_{0} \ \),\( \ \delta \ \),\( \ \phi \ \)を用いて,\( \ I_{\mathrm {a}}X_{\mathrm {s}} \ \)および\( \ V \ \)を表す式を導出せよ。
(3) 定格皮相電力\( \ 120 \ 000 \ \mathrm {[kV\cdot A]} \ \),定格電圧\( \ 13.8 \ \mathrm {[kV]} \ \),同期リアクタンス\( \ 1.8 \ \mathrm {[p.u.]} \ \)の三相同期発電機について,無負荷状態で端子電圧が\( \ 1.3 \ \mathrm {[p.u.]} \ \)になるように界磁電流を調整して,界磁電流をそのままに保って三相平衡負荷を発電機端子に接続したところ,発電機の負荷角(内部相差角)は\( \ 30 \ [°] \ \)で力率は\( \ 0.9 \ \)であった。この運転状態における電機子電流\( \ \mathrm {[p.u.]} \ \)および端子電圧\( \ \mathrm {[p.u.]} \ \)を求めよ。
(4) \( \ E_{0} \ \),\( \ V \ \),\( \ \delta \ \),\( \ X_{\mathrm {s}} \ \)を用いて,発電機出力\( \ P \ \)を表す式を単位法にて導出せよ。
(5) 上記(4)で導出した式を用いて,上記(3)の状態における発電機出力\( \ P \ \mathrm {[kW]} \ \)を求めよ。
【ワンポイント解説】
(1),(2)は\( \ 1 \ \)種としては非常に易しい問題で,(3)以降もそれほど難解な問題はありません。
(3)の問題文で\( \ E_{0}=1.3 \ \mathrm {[p.u.]} \ \)が読み解けるかがこの問題のカギとなりそうです。
1.電圧変動率\( \ \varepsilon \ \)の定義
無負荷誘導起電力(相電圧)を\( \ E \ \),端子電圧(相電圧)を\( \ V \ \)とすると,電圧変動率\( \ \varepsilon \ \)は,
\[
\begin{eqnarray}
\varepsilon &=&\frac {E-V}{V}\times 100 \ [%] \\[ 5pt ]
\end{eqnarray}
\]
と定義されます。
2.単位法における同期発電機の出力\( \ P \ \)
無負荷誘導起電力(相電圧)を\( \ E \ \),端子電圧(相電圧)を\( \ V \ \),電機子電流\( \ I \ \),同期リアクタンスを\( \ X_{\mathrm {S}} \ \),内部相差角を\( \ \delta \ \),力率角を\( \ \phi \ \)とすると,出力\( \ P \ \)は,
\[
\begin{eqnarray}
P&=&VI\cos\phi \\[ 5pt ]
&=&\frac {EV}{X_{\mathrm {S}}}\sin {\delta } \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)電圧変動率\( \ [%] \ \)の算出式を図に記載された記号を用いて示す
電圧変動率\( \ \varepsilon \ \)とすると,電圧変動率の定義より,
\[
\begin{eqnarray}
\varepsilon &=&\frac {E_{0}-V}{V}\times 100 \ [%] \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)\( \ I_{\mathrm {a}}X_{\mathrm {s}} \ \)および\( \ V \ \)を表す式
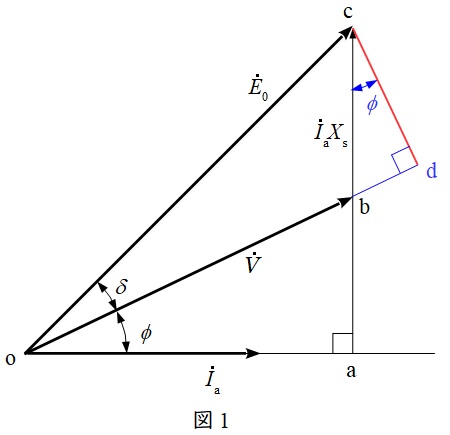
設問の図を図1のように補助線を引く。
図1より,線分\( \ \mathrm {cd} \ \)の長さは,
\[
\begin{eqnarray}
\mathrm {cd}&=&E_{0}\sin \delta \\[ 5pt ]
&=&I_{\mathrm {a}}X_{\mathrm {s}}\cos \phi \\[ 5pt ]
\end{eqnarray}
\]
となるから,\( \ I_{\mathrm {a}}X_{\mathrm {s}} \ \)について整理すると,
\[
\begin{eqnarray}
I_{\mathrm {a}}X_{\mathrm {s}}&=&E_{0} \frac {\sin \delta }{\cos \phi } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,線分\( \ \mathrm {oa} \ \)の長さは,
\[
\begin{eqnarray}
\mathrm {oa}&=&E_{0}\cos \left( \delta +\phi \right) \\[ 5pt ]
&=&V\cos \phi \\[ 5pt ]
\end{eqnarray}
\]
となるから,\( \ V \ \)について整理すると,
\[
\begin{eqnarray}
V&=&E_{0}\frac {\cos \left( \delta +\phi \right) }{\cos \phi} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)指定された運転状態における電機子電流\( \ \mathrm {[p.u.]} \ \)および端子電圧\( \ \mathrm {[p.u.]} \ \)
(2)解答より,
\[
\begin{eqnarray}
I_{\mathrm {a}}X_{\mathrm {s}}&=&E_{0} \frac {\sin \delta }{\cos \phi } \\[ 5pt ]
\end{eqnarray}
\]
であるから,電機子電流\( \ I_{\mathrm {a}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {a}}&=&\frac {E_{0}\sin \delta }{X_{\mathrm {s}}\cos \phi } \\[ 5pt ]
\end{eqnarray}
\]
となる。題意より,\( \ X_{\mathrm {s}}=1.8 \ \mathrm {[p.u.]} \ \),\( \ E_{0}=1.3 \ \mathrm {[p.u.]} \ \),\( \ \cos \phi =0.9 \ \),\( \ \delta =30° \ \)を代入すると,
\[
\begin{eqnarray}
I_{\mathrm {a}}&=&\frac {1.3\sin 30° }{1.8\times 0.9} \\[ 5pt ]
&≒&0.401 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,\( \ V \ \)は加法定理より,
\[
\begin{eqnarray}
V&=&E_{0}\frac {\cos \left( \delta +\phi \right) }{\cos \phi} \\[ 5pt ]
&=&E_{0}\frac {\cos \delta \cos \phi \ – \sin \delta \sin \phi }{\cos \phi} \\[ 5pt ]
\end{eqnarray}
\]
と整理でき,同様に各値を代入すると,
\[
\begin{eqnarray}
V&=&1.3 \times \frac {\cos 30° \times 0.9 \ – \sin 30° \times \sqrt {1-0.9^{2}} }{0.9} \\[ 5pt ]
&≒&0.811 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)発電機出力\( \ P \ \)を表す式
単位法において発電機出力\( \ P \ \)は,
\[
\begin{eqnarray}
P&=&VI_{\mathrm {a}}\cos \phi \\[ 5pt ]
\end{eqnarray}
\]
であるから,この式に\( \ \displaystyle I_{\mathrm {a}}=\frac {E_{0}\sin \delta }{X_{\mathrm {s}}\cos \phi } \ \)を代入すると,
\[
\begin{eqnarray}
P&=&V\frac {E_{0}\sin \delta }{X_{\mathrm {s}}\cos \phi }\cos \phi \\[ 5pt ]
&=&\frac {VE_{0}\sin \delta }{X_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)上記(3)の状態における発電機出力\( \ P \ \mathrm {[kW]} \ \)
(4)で導出した式に各値を代入すると,
\[
\begin{eqnarray}
P&=&\frac {VE_{0}\sin \delta }{X_{\mathrm {s}}} \\[ 5pt ]
&=&\frac {0.8110 \times 1.3 \sin 30° }{1.8} \\[ 5pt ]
&≒&0.2929 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,定格皮相電力が\( \ 120 \ 000 \ \mathrm {[kV\cdot A]} \ \)であるから,
\[
\begin{eqnarray}
P&=&0.2929 \times 120 \ 000 \\[ 5pt ]
&≒& 35 \ 100 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん