【問題】
【難易度】★★★☆☆(普通)
次の文章は,電力系統の潮流調整に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)の\((1)\)から\((3)\)については,最も適切な語句を解答群の中から選び,その記号を記述用紙の解答欄に,文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)の\((4)\)から\((7)\)については,当てはまる式を記述用紙の解答欄に記入しなさい。
ループ系統の運用にあたっては,電力潮流が線路容量を超過しないよう,他の系統からの回り込みも考慮しつつ適切な潮流管理を行う必要がある。リアクタンス成分が支配的である一般的な電力系統においては,系統の地点間の\( \ \fbox { (1) } \ \)によって有効電力潮流が,そして電圧差によって無効電力潮流が調整できる。ループ潮流を調整する手段として,発電機の出力調整の他に,ループを構成する系統のリアクタンスを調整する\( \ \fbox { (2) } \ \)や,\( \ \fbox { (1) } \ \)を調整する\( \ \fbox { (3) } \ \)が用いられる場合がある。
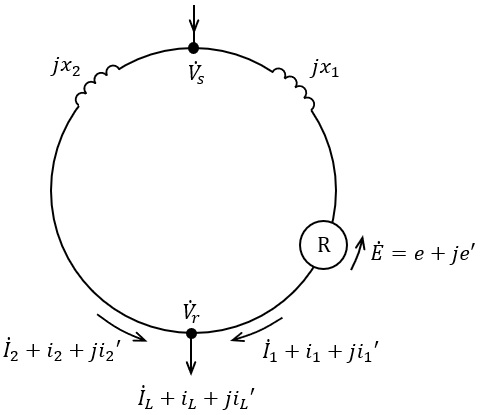
これを用いた潮流調整の原理を図の系統を例にして考える。図のループ系統において,負荷電流\( \ {\dot I}_{L} \ \)が\( \ {\dot I}_{1} \ \)と\( \ {\dot I}_{2} \ \)に分流し,ループの両端には\( \ {\dot V}_{s}-{\dot V}_{r} \ \)の電圧差(線間電圧)が生じている。ここで図中\( \ \mathrm {R} \ \)が\( \ \fbox { (3) } \ \)であり,その両端に発生する電圧\( \ \dot E \ \)を変化させるとき,
\( \ {\dot I}_{L}=i_{L}+j{i_{L}}^{\prime } \ \),\( \ \dot E=e+je^{\prime } \ \)を用いて,\( \ {\dot I}_{1}=i_{1}+j{i_{1}}^{\prime } \ \)を表わすと,
\[
\begin{eqnarray}
i_{1} &=& \ \fbox { (4) } \ i_{L}- \ \fbox { (5) } \ e^{\prime } \\[ 5pt ]
{i_{1}}^{\prime } &=& \ \fbox { (6) } \ {i_{L}}^{\prime }+ \ \fbox { (7) } \ e \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ {\dot I}_{L} \ \)が一定であっても,\( \ \dot E \ \)を制御することで,\( \ {\dot I}_{1} \ \),\( \ {\dot I}_{2} \ \)を調整できることがわかる。
〔問6の\((1)\)から\((3)\)までの解答群〕
\[
\begin{eqnarray}
&(イ)& 背後インピーダンス差 &(ロ)& 位相調整変圧器 &(ハ)& 周波数差 \\[ 5pt ]
&(ニ)& 可変速揚水発電機 &(ホ)& 相差角 &(ヘ)& 周波数変換器 \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
&(ト)& \mathrm {SVC \ \left( Static \ Var \ Compensator \right) } \\[ 5pt ]
&(チ)& \mathrm {TCSC \ \left( Thyristor \ Controlled \ Series \ Capacitor \right) } \\[ 5pt ]
&(リ)& \mathrm {BTB \ \left( Back \ to \ Back \right) } \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
電力系統における有効電力潮流と無効電力潮流の調整方法に関する問題です。
前半の(1)~(3)まではある程度知識として覚えておかなければなりませんが,後半の計算問題(\( \ 12 \ \)点分)は確実に正答しておきたいです。\( \ 1 \ \)種攻略のためには問題文を理解しながら解いていく能力が必要となります。
1.複素電力
三相線路において,送電端電圧(相電圧)を\( \ {\dot E}_{\mathrm {s}} \ \mathrm {[V]} \ \),受電端電圧(相電圧)を\( \ {\dot E}_{\mathrm {r}} \ \mathrm {[V]} \ \),線路電流を\( \ \dot I \ \mathrm {[A]} \ \)とすると,受電端への送電電力\( \ P+\mathrm {j}Q \ \mathrm {[V\cdot A]} \ \)は遅れ無効電力を正とすると,
\[
\begin{eqnarray}
P+\mathrm {j}Q&=&3{\dot E}_{\mathrm {r}}\overline {\dot I} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。ただし,\( \ \overline {\dot I} \ \)は\( \ \dot I \ \)の共役複素数であり,\( \ \dot I =I_{\mathrm {r}}+\mathrm {j}I_{\mathrm {i}} \ \)であるとき,\( \ \overline {\dot I}=I_{\mathrm {r}}-\mathrm {j}I_{\mathrm {i}} \ \)となります。
2.無限大母線に接続するときの有効電力\( \ P \ \)と無効電力\( \ Q \ \)
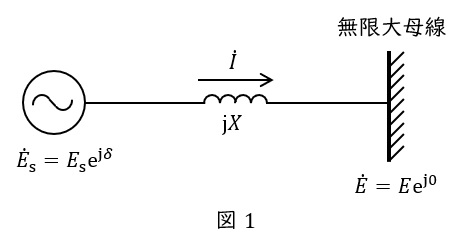
図1のような無限大母線(相電圧\( \ \dot E=E\mathrm {e}^{\mathrm {j}0}=E \ \))にリアクタンス\( \ X \ \)を介して接続する発電機(相電圧\( \ {\dot E}_{\mathrm {s}}=E_{\mathrm {s}}\mathrm {e}^{\mathrm {j}\delta } \ \))の三相の複素電力\( \ P+\mathrm {j}Q \ \)を考えます。ただし,線路等の抵抗分は十分小さく無視するものとします。
リアクタンスを流れる電流を\( \ \dot I \ \)とすると,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {s}}-\dot E&=&\mathrm {j}X\dot I \\[ 5pt ]
\dot I&=&\frac {{\dot E}_{\mathrm {s}} -\dot E}{\mathrm {j}X} \\[ 5pt ]
\dot I&=&\frac {E_{\mathrm {s}}\mathrm {e}^{\mathrm {j}\delta } -E}{\mathrm {j}X} \\[ 5pt ]
\end{eqnarray}
\]
となり,複素電力\( \ P+\mathrm {j}Q \ \)は,
\[
\begin{eqnarray}
P+\mathrm {j}Q&=&3\dot E\overline {\dot I} \\[ 5pt ]
&=&3E\cdot \frac {E_{\mathrm {s}}\mathrm {e}^{-\mathrm {j}\delta } -E}{-\mathrm {j}X} \\[ 5pt ]
&=&\mathrm {j}3E\cdot \frac {E_{\mathrm {s}}\left( \cos \delta -\mathrm {j}\sin \delta \right) -E}{X} \\[ 5pt ]
&=&\frac {\mathrm {j}3E_{\mathrm {s}}E\left( \cos \delta -\mathrm {j}\sin \delta \right) -\mathrm {j}3E^{2}}{X} \\[ 5pt ]
&=&\frac {\mathrm {j}3E_{\mathrm {s}}E\cos \delta +3E_{\mathrm {s}}E\sin \delta -\mathrm {j}3E^{2}}{X} \\[ 5pt ]
&=&\frac {3E_{\mathrm {s}}E\sin \delta + \mathrm {j}3\left( E_{\mathrm {s}}E\cos \delta -E^{2}\right) }{X} \\[ 5pt ]
&=&\frac {3E_{\mathrm {s}}E\sin \delta }{X}+\mathrm {j}\frac {3\left( E_{\mathrm {s}}E\cos \delta -E^{2}\right) }{X} \\[ 5pt ]
\end{eqnarray}
\]
となります。両辺比較すると,
\[
\begin{eqnarray}
P&=&\frac {3E_{\mathrm {s}}E\sin \delta }{X} \\[ 5pt ]
Q&=&\frac {3\left( E_{\mathrm {s}}E\cos \delta -E^{2}\right) }{X} \\[ 5pt ]
\end{eqnarray}
\]
と求められます。ここで,線間電圧の大きさ\( \ V_{\mathrm {s}}=\sqrt {3}E_{\mathrm {s}} \ \),\( \ V=\sqrt {3}E \ \)とすれば,
\[
\begin{eqnarray}
P&=&\frac {V_{\mathrm {s}}V\sin \delta }{X} \\[ 5pt ]
Q&=&\frac { V_{\mathrm {s}}V\cos \delta -V^{2} }{X} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:ホ
題意より解答候補は,(イ)背後インピーダンス差,(ハ)周波数差,(ホ)相差角,になると思います。
ワンポイント解説「2.無限大母線に接続するときの有効電力\( \ P \ \)と無効電力\( \ Q \ \)」の通り,有効電力\( \ P \ \)は,
\[
\begin{eqnarray}
P&=&\frac {V_{s}V_{r}\sin \delta }{X} \\[ 5pt ]
\end{eqnarray}
\]
で求められ,相差角\( \ \delta \ \)が十分に小さければ\( \ \sin \delta ≒\delta \ \)と近似できるので,
\[
\begin{eqnarray}
P&=&\frac {V_{s}V_{r}}{X}\cdot \delta \\[ 5pt ]
\end{eqnarray}
\]
となり,有効電力潮流が相差角\( \ \delta \ \)により調整できることになります。
【参考】
無効電力\( \ Q \ \)は,
\[
\begin{eqnarray}
Q&=&\frac { V_{s}V_{r}\cos \delta -V_{r}^{2} }{X} \\[ 5pt ]
\end{eqnarray}
\]
で求められ,相差角\( \ \delta \ \)が十分に小さければ\( \ \cos \delta ≒1 \ \)と近似できるので,
\[
\begin{eqnarray}
Q&=&\frac { V_{s}V_{r} -V_{r}^{2} }{X} \\[ 5pt ]
&=&\frac {V_{r}}{X}\cdot \left( V_{s} -V_{r}\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ V_{r} \ \)がほぼ一定であるとすれば,無効電力潮流が電圧差によって調整できることになります。
(2)解答:チ
題意より解答候補は,(ト)\( \ \mathrm {SVC \ \left( Static \ Var \ Compensator \right) } \ \),(チ)\( \ \mathrm {TCSC \ \left( Thyristor \ Controlled \ Series \ Capacitor \right) } \ \),(リ)\( \ \mathrm {BTB \ \left( Back \ to \ Back \right) } \ \),になると思います。
このうち,サイリスタの点弧角によりループを構成する系統のリアクタンスを調整するのは\( \ \mathrm {TCSC \ \left( Thyristor \ Controlled \ Series \ Capacitor \right) } \ \)(サイリスタ制御直列コンデンサ)です。中身の構造は理解する必要はありません。
(3)解答:ロ
題意より解答候補は,(ロ)位相調整変圧器,(ニ)可変速揚水発電機,(ヘ)周波数変換器,になると思います。
このうち相差角を調整できるのは,ループ系統の位相を調整し,ループ潮流を調整可能な位相調整変圧器となります。
(4)解答:\( \ \displaystyle \frac {x_{2}}{x_{1}+x_{2}} \ \)
\( \ {\dot V}_{s}-{\dot V}_{r} \ \)を求める式より,
\[
\begin{eqnarray}
\dot E+jx_{1}{\dot I}_{1}&=&jx_{2}{\dot I}_{2} \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ {\dot I}_{1}+{\dot I}_{2}={\dot I}_{L} \ \)であるから,
\[
\begin{eqnarray}
\dot E+jx_{1}{\dot I}_{1} &=&jx_{2}\left( {\dot I}_{L}-{\dot I}_{1}\right) \\[ 5pt ]
&=&jx_{2}{\dot I}_{L} -jx_{2}{\dot I}_{1} \\[ 5pt ]
jx_{1}{\dot I}_{1}+jx_{2}{\dot I}_{1}&=&jx_{2}{\dot I}_{L} -\dot E \\[ 5pt ]
j\left( x_{1}+x_{2}\right) {\dot I}_{1}&=&jx_{2}{\dot I}_{L} -\dot E \\[ 5pt ]
{\dot I}_{1}&=&\frac {x_{2}}{x_{1}+x_{2}}{\dot I}_{L} -\frac {1}{j\left( x_{1}+x_{2}\right)}\dot E \\[ 5pt ]
&=&\frac {x_{2}}{x_{1}+x_{2}}{\dot I}_{L} +j\frac {1}{ x_{1}+x_{2}}\dot E \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ {\dot I}_{L}=i_{L}+j{i_{L}}^{\prime } \ \),\( \ \dot E=e+je^{\prime } \ \)及び\( \ {\dot I}_{1}=i_{1}+j{i_{1}}^{\prime } \ \)を代入すると,
\[
\begin{eqnarray}
i_{1}+j{i_{1}}^{\prime }&=&\frac {x_{2}}{x_{1}+x_{2}}\left( i_{L}+j{i_{L}}^{\prime }\right) +j\frac {1}{ x_{1}+x_{2}}\left( e+je^{\prime }\right) \\[ 5pt ]
&=&\frac {x_{2}}{x_{1}+x_{2}}i_{L}+j\frac {x_{2}}{x_{1}+x_{2}}{i_{L}}^{\prime } +j\frac {1}{x_{1}+x_{2}}e-\frac {1}{x_{1}+x_{2}}e^{\prime } \\[ 5pt ]
&=&\frac {x_{2}}{x_{1}+x_{2}}i_{L}-\frac {1}{x_{1}+x_{2}}e^{\prime }+j\left(\frac {x_{2}}{x_{1}+x_{2}}{i_{L}}^{\prime } +\frac {1}{x_{1}+x_{2}}e\right)
\end{eqnarray}
\]
となり,実部虚部を比較すれば,
\[
\begin{eqnarray}
i_{1}&=&\frac {x_{2}}{x_{1}+x_{2}}i_{L}-\frac {1}{x_{1}+x_{2}}e^{\prime } \\[ 5pt ]
{i_{1}}^{\prime }&=&\frac {x_{2}}{x_{1}+x_{2}}{i_{L}}^{\prime } +\frac {1}{x_{1}+x_{2}}e \\[ 5pt ]
\end{eqnarray}
\]
と求められる。したがって,\( \ i_{L} \ \)の係数は\( \ \displaystyle \frac {x_{2}}{x_{1}+x_{2}} \ \)と求められる。
(5)解答:\( \ \displaystyle \frac {1}{x_{1}+x_{2}} \ \)
(4)解答式より,\( \ e^{\prime } \ \)の係数は\( \ \displaystyle \frac {1}{x_{1}+x_{2}} \ \)と求められる。
(6)解答:\( \ \displaystyle \frac {x_{2}}{x_{1}+x_{2}} \ \)
(4)解答式より,\( \ {i_{L}}^{\prime } \ \)の係数は\( \ \displaystyle \frac {x_{2}}{x_{1}+x_{2}} \ \)と求められる。
(7)解答:\( \ \displaystyle \frac {1}{x_{1}+x_{2}} \ \)
(4)解答式より,\( \ e \ \)の係数は\( \ \displaystyle \frac {1}{x_{1}+x_{2}} \ \)と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん