《電力》〈送電〉[H27:問5] 架空送電線の電気的定数に関する空欄穴埋問題

1 【問題】
2 【ワンポイント解説】
3 【用語の解説】
- 3.1 【関連する「電気の神髄」記事】
4 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，架空送電線の電気的定数に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。

架空送電線では，可とう性などの理由から，一般により線が用いられるが，この場合，素線の実長は中心導体に比べて若干長くなるので，その分抵抗が大きくなる。この割合を$ \ \fbox {　（１）　} \ $といい，通常は2％程度である。一方で，電線に交流が流れると電流は断面全体にわたって一様に流れず，$ \ \fbox {　（２）　} \ $多く流れる。この現象を$ \ \fbox {　（３）　} \ $といい，このため抵抗が増加する。この際電流の流れる部分の深さ$ \ \delta \ [\mathrm {m}] \ $は角周波数を$ \ \omega \ [\mathrm {rad/s}] \ $，透磁率を$ \ \mu \ [\mathrm {H/m}] \ $，導電率を$ \ \sigma \ [\mathrm {S/m}] \ $とすれば$ \ \fbox {　（４）　} \ [\mathrm {m}] \ $と表される。

一方，電線(単導体)1本の単位長当たりの作用インダクタンス$ \ L \ [\mathrm {mH/km}] \ $は比透磁率$ \ \mu _{\mathrm {s}} \ $，線間距離$ \ D \ [\mathrm {m}] \ $，電線半径$ \ r \ [\mathrm {m}] \ $として$ \ \fbox {　（５）　} \ [\mathrm {mH/km}] \ $と表される。架空送電線の作用インダクタンスの値は$ \ \fbox {　（６）　} \ \mathrm {mH/km} \ $程度である。

また，電線(単導体)1本の単位長当たりの作用静電容量$ \ C \ [\mathrm {\mu F/km}] \ $は比誘電率$ \ \varepsilon _{\mathrm {s}} \ $，線間距離$ \ D \ [\mathrm {m}] \ $，電線半径$ \ r \ [\mathrm {m}] \ $を用いて$ \ \fbox {　（７）　} \ [\mathrm {\mu F/km}] \ $と表される。架空送電線の作用静電容量の値は$ \ 0.008～0.01 \ \mathrm {\mu F/km} \ $程度である。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　0.1　　　　　&（ロ）&　より込み率 \\[ 5pt ] &（ハ）&　抵抗率　　　　　&（ニ）&　C=\frac {0.02413\varepsilon _{\mathrm {s}}}{\log _{10}(rD)} \\[ 5pt ] &（ホ）&　1　　　　　&（ヘ）&　表面に近くなるほど \\[ 5pt ] &（ト）&　10　　　　　&（チ）&　近接効果 \\[ 5pt ] &（リ）&　\delta = \sqrt{\frac {\omega \mu \sigma }{2}}　　　　　&（ヌ）&　ゼーベック効果 \\[ 5pt ] &（ル）&　\delta = \sqrt{\frac {2}{\omega \mu \sigma }}　　　　　&（ヲ）&　アスペクト比 \\[ 5pt ] &（ワ）&　C=\frac {0.02413\varepsilon _{\mathrm {s}}}{\log _{10}(\frac {r}{D})}　　　　　&（カ）&　L=0.05\mu _{\mathrm {s}}+0.4605 \log _{10}\frac {D}{r} \\[ 5pt ] &（ヨ）&　C=\frac {0.02413\varepsilon _{\mathrm {s}}}{\log _{10}(\frac {D}{r})}　　　　　&（タ）&　中心に近づくほど \\[ 5pt ] &（レ）&　L=0.05\mu _{\mathrm {s}}+0.4605 \log _{10}\frac {r}{D}　　　　　&（ソ）&　表皮効果 \\[ 5pt ] &（ツ）&　より線と中心導体の接点で　　　　　&（ネ）&　\delta = \sqrt{\frac {2\sigma }{\omega \mu }} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

本問の後半部分は難しめの内容で，詳しくは専門書に書いてあるような内容です。専門家であれば，細かい数字まで理解する必要があると思いますが，電験対策としてはあまり深追いをせず，線間距離や電線半径が変わった場合にどうなるかを電磁気の知識を利用してイメージできるようにしましょう。

【用語の解説】

（ロ）より込み率
送電線の素線の長さはより合わせることにより送電線より長くなりますが，その長さの比をより込み率と言います。
（チ）近接効果
　電線同士の距離が近くなると，それぞれの磁界の影響が無視できなくなり，各電線に影響が出ることを言います。
（ヌ）ゼーベック効果
　異種金属で閉回路を作り，温度差をつけると起電力が生じます。熱電対の原理となっています。
（ヲ）アスペクト比
　縦横比のことで，テレビ画面等で使用されます。
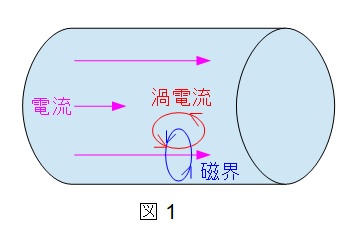
（ソ）表皮効果
　交流電流において，導体内の電流分布が外側に集中する現象で，図1のように電磁誘導により導体内に渦電流が発生することで生じます。角周波数と透磁率，導電率が大きくなるほど顕著となります。

【解答】

(1)解答：ロ
題意より，解答候補は（ロ）より込み率，（ハ）抵抗率，（ヲ）アスペクト比，となると思いますが，題意と合うのはより込み率となります。

(2)解答：ヘ
(3)解答：ソ
題意より，(2)の解答候補は（ヘ）表面に近くなるほど，（タ）中心に近づくほど，（ツ）より線と中心導体の接点で，(3)の解答候補は（チ）近接効果，（ヌ）ゼーベック効果，（ソ）表皮効果，になると思いますが，用語の解説の通り，表皮効果は表面に近づくほど電流が大きくなる現象となります。

(4)解答：ル
表皮効果は，角周波数と透磁率，導電率が大きくなるほど顕著となります。直流(周波数零)で発生しない，電磁誘導は透磁率が大きく，導電率が大きいほど発生しやすいをイメージできれば，解答は選択できると思います。

(5)解答：カ
題意より，解答候補は$（カ）\displaystyle L=0.05\mu _{\mathrm {s}}+0.4605 \log _{10}\frac {D}{r} \ $，$（レ）\displaystyle L=0.05\mu _{\mathrm {s}}+0.4605 \log _{10}\frac {r}{D} \ $，となると思います。作用インダクタンスは$（カ）\displaystyle L=0.05\mu _{\mathrm {s}}+0.4605 \log _{10}\frac {D}{r}$の通りとなりますが，$D≫r$なので，$（レ）\displaystyle L=0.05\mu _{\mathrm {s}}+0.4605 \log _{10}\frac {r}{D}$であると値が負となってしまうことからも消去法で求めることができます。

(6)解答：ホ
架空送電線でのインダクタンスは$ \ 1.0 \ \mathrm {mH/km} \ $程度となります。

(7)解答：ヨ
詳細は専門書レベルになりますので，ここでの説明は割愛しますが，図2のような同心軸ケーブルの静電容量が$ \ \displaystyle C= \frac {2\pi \varepsilon }{\displaystyle \ln \frac {b}{a}} \ $となることから想像できると良いと思います。