【問題】
【難易度】★★★☆☆(普通)
次の文章は,中距離送電線の四端子定数に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
こう長が\( \ 50\sim 100 \ \mathrm {km} \ \)の中距離送電線は,図のような\( \ \pi \ \)形等価回路として模擬することができる。すなわち,送電線路上の直列インピーダンス及び並列アドミタンスを\( \ \fbox { (1) } \ \)定数として取り扱うことが可能である。
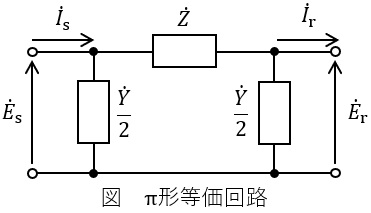
送電端の相電圧\( \ {\dot E}_{\mathrm {s}} \ \),電流\( \ {\dot I}_{\mathrm {s}} \ \)と受電端の相電圧\( \ {\dot E}_{\mathrm {r}} \ \),電流\( \ {\dot I}_{\mathrm {r}} \ \)の関係は,送電線の四端子定数\( \ \dot A \ \),\( \ \dot B \ \),\( \ \dot C \ \),\( \ \dot D \ \)を用いて,以下のとおり表すことができる。
\[
\begin{eqnarray}
\begin{bmatrix}
{\dot E}_{\mathrm {s}} \\
{\dot I}_{\mathrm {s}}
\end{bmatrix}&=&\begin{bmatrix}
\dot A & \dot B \\
\dot C & \dot D
\end{bmatrix}\begin{bmatrix}
{\dot E}_{\mathrm {r}} \\
{\dot I}_{\mathrm {r}}
\end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
ここで四端子定数\( \ \dot A \ \),\( \ \dot B \ \),\( \ \dot C \ \),\( \ \dot D \ \)は,直列インピーダンス\( \ \dot Z \ \)及び並列アドミタンス\( \ \dot Y \ \)を用いて以下のとおり表すことができる。
\[
\begin{eqnarray}
\dot A &=& \dot D = \ \fbox { (2) } \ \\[ 5pt ]
\dot B &=& \ \fbox { (3) } \ \\[ 5pt ]
\dot C &=& \ \fbox { (4) } \ \\[ 5pt ]
\end{eqnarray}
\]
公称電圧\( \ 275 \ \mathrm {kV} \ \)の三相交流中距離送電線において,\( \ \dot Z=\mathrm {j}20 \ \mathrm {\Omega } \ \),\( \ \dot Y=\mathrm {j}0.001 \ \mathrm {S} \ \),送電端の相電圧\( \ {\dot E}_{\mathrm {s}}=\displaystyle \frac {275}{\sqrt {3}} \ \mathrm {kV} \ \)のとき,受電端を無負荷とした場合の受電端の相電圧\( \ {\dot E}_{\mathrm {r}} \ \)は\( \ \fbox { (5) } \ \mathrm {kV} \ \)となる。
〔問2の解答群〕
\[
\begin{eqnarray}
&(イ)& 1+\frac {\dot Z\dot Y}{4} &(ロ)& \dot Y \left( 1+\frac {\dot Z\dot Y}{2}\right) &(ハ)& \dot Y \\[ 5pt ]
&(ニ)& 分布 &(ホ)& 162 &(ヘ)& 集中 \\[ 5pt ]
&(ト)& \dot Y \left( 1+\dot Z\dot Y\right) &(チ)& 伝搬 &(リ)& \dot Z \\[ 5pt ]
&(ヌ)& 164 &(ル)& 1+\dot Z\dot Y &(ヲ)& 160 \\[ 5pt ]
&(ワ)& \dot Y \left( 1+\frac {\dot Z\dot Y}{4}\right) &(カ)& 1 &(ヨ)& 1+\frac {\dot Z\dot Y}{2} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
\( \ \pi \ \)形等価回路を用いた中距離送電線の四端子定数に関する問題です。
\( \ 1 \ \)種では\( \ \pi \ \)形等価回路と\( \ \mathrm {T} \ \)形等価回路を扱う問題が出題されます。
二次試験では難解な計算問題も出題されたことがありますが,ひとまず一次試験においては一般的な回路計算のように扱えばよいと理解しておけばよいでしょう。
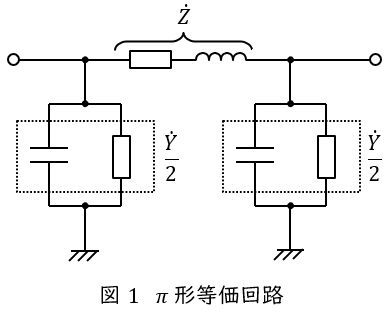
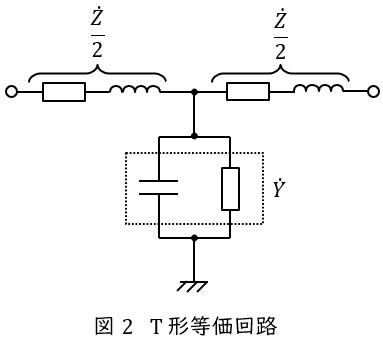
1.\( \ \pi \ \)形等価回路と\( \ \mathrm {T} \ \)形等価回路
送電線のこう長が大きくなると送電線のリアクタンスや静電容量が無視できなくなるので,線路定数を集中定数として扱い\( \ \pi \ \)形等価回路や\( \ \mathrm {T} \ \)形等価回路を適用します。送電線のインピーダンスを\( \ \dot Z \ \),アドミタンスを\( \ \dot Y \ \)とすると,\( \ \pi \ \)形等価回路は図1,\( \ \mathrm {T} \ \)形等価回路は図2のようになります。
電験では送電線の抵抗分やサセプタンス分は無視し,送電線のインダクタンスを\( \ L \ \mathrm {[H]} \ \),静電容量を\( \ C \ \mathrm {[F]} \ \)として,
\[
\begin{eqnarray}
{\dot Z}&=&\mathrm {j}\omega L \\[ 5pt ]
{\dot Y}&=&\mathrm {j}\omega C \\[ 5pt ]
\end{eqnarray}
\]
として扱う問題がほとんどです。
【解答】
(1)解答:ヘ
題意より解答候補は,(ニ)分布,(ヘ)集中,(チ)伝搬,になると思います。
\( \ \pi \ \)形等価回路は,中距離送電線を定数として模擬し,集中定数として取り扱うことができます。
(2)解答:ヨ
右側のアドミタンス\( \ \displaystyle \frac {\dot Y}{2} \ \)を流れる電流\( \ {\dot I}_{2} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{2}&=&\frac {\dot Y}{2}{\dot E}_{\mathrm {r}} \\[ 5pt ]
\end{eqnarray}
\]
となるので\( \ {\dot E}_{\mathrm {s}} \ \)は,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {s}}&=&{\dot E}_{\mathrm {r}}+\dot Z \left( {\dot I}_{2}+{\dot I}_{\mathrm {r}}\right) \\[ 5pt ]
&=&{\dot E}_{\mathrm {r}}+\dot Z \left( \frac {\dot Y}{2}{\dot E}_{\mathrm {r}}+{\dot I}_{\mathrm {r}}\right) \\[ 5pt ]
&=&{\dot E}_{\mathrm {r}}+ \frac {\dot Z\dot Y}{2}{\dot E}_{\mathrm {r}}+\dot Z{\dot I}_{\mathrm {r}} \\[ 5pt ]
&=&\left( 1+ \frac {\dot Z\dot Y}{2}\right) {\dot E}_{\mathrm {r}}+\dot Z{\dot I}_{\mathrm {r}} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \displaystyle \dot A =1+ \frac {\dot Z\dot Y}{2} \ \)と求められる。
(3)解答:リ
(2)解答式より,\( \ \displaystyle \dot B =\dot Z \ \)と求められる。
(4)解答:ワ
左側のアドミタンス\( \ \displaystyle \frac {\dot Y}{2} \ \)を流れる電流\( \ {\dot I}_{1} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{1}&=&\frac {\dot Y}{2}{\dot E}_{\mathrm {s}} \\[ 5pt ]
&=&\frac {\dot Y}{2}\left\{ \left( 1+ \frac {\dot Z\dot Y}{2}\right) {\dot E}_{\mathrm {r}}+\dot Z{\dot I}_{\mathrm {r}}\right\} \\[ 5pt ]
&=&\frac {\dot Y}{2}\left( 1+ \frac {\dot Z\dot Y}{2}\right) {\dot E}_{\mathrm {r}}+\frac {\dot Z\dot Y}{2}{\dot I}_{\mathrm {r}} \\[ 5pt ]
\end{eqnarray}
\]
となるので\( \ {\dot I}_{\mathrm {s}} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {s}}&=&{\dot I}_{1}+{\dot I}_{2}+{\dot I}_{\mathrm {r}} \\[ 5pt ]
&=&\frac {\dot Y}{2}\left( 1+ \frac {\dot Z\dot Y}{2}\right) {\dot E}_{\mathrm {r}}+\frac {\dot Z\dot Y}{2}{\dot I}_{\mathrm {r}}+\frac {\dot Y}{2}{\dot E}_{\mathrm {r}}+{\dot I}_{\mathrm {r}} \\[ 5pt ]
&=&\frac {\dot Y}{2}\left( 1+ \frac {\dot Z\dot Y}{2}+1\right) {\dot E}_{\mathrm {r}}+\left( 1+\frac {\dot Z\dot Y}{2}\right) {\dot I}_{\mathrm {r}} \\[ 5pt ]
&=&\frac {\dot Y}{2}\left( 2+ \frac {\dot Z\dot Y}{2}\right) {\dot E}_{\mathrm {r}}+\left( 1+\frac {\dot Z\dot Y}{2}\right) {\dot I}_{\mathrm {r}} \\[ 5pt ]
&=&\dot Y\left( 1+ \frac {\dot Z\dot Y}{4}\right) {\dot E}_{\mathrm {r}}+\left( 1+\frac {\dot Z\dot Y}{2}\right) {\dot I}_{\mathrm {r}} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \displaystyle \dot C =\dot Y\left( 1+ \frac {\dot Z\dot Y}{4}\right) \ \)と求められる。
(5)解答:ヲ
問題の条件における四端子定数は,
\[
\begin{eqnarray}
\dot A =\dot D &=&1+ \frac {\dot Z\dot Y}{2} \\[ 5pt ]
&=&1+ \frac {\mathrm {j}20\times \mathrm {j}0.001}{2} \\[ 5pt ]
&=&0.99 \\[ 5pt ]
\dot B &=&\dot Z \\[ 5pt ]
&=&\mathrm {j}20 \\[ 5pt ]
\dot C &=&\dot Y\left( 1+ \frac {\dot Z\dot Y}{4}\right) \\[ 5pt ]
&=&\mathrm {j}0.001\times \left( 1+ \frac {\mathrm {j}20\times \mathrm {j}0.001}{4}\right) \\[ 5pt ]
&=&\mathrm {j}0.000 \ 995 \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
\begin{bmatrix}
{\dot E}_{\mathrm {s}} \\
{\dot I}_{\mathrm {s}}
\end{bmatrix}&=&\begin{bmatrix}
0.99 & \mathrm {j}20 \\
\mathrm {j}0.000 \ 995 & 0.99
\end{bmatrix}\begin{bmatrix}
{\dot E}_{\mathrm {r}} \\
{\dot I}_{\mathrm {r}}
\end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となる。受電端を無負荷とした場合\( \ {\dot I}_{\mathrm {r}}=0 \ \)であるので,\( \ {\dot E}_{\mathrm {s}}=\displaystyle \frac {275}{\sqrt {3}} \ \mathrm {kV} \ \)のときの受電端電圧\( \ {\dot E}_{\mathrm {r}} \ \)は,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {s}}&=&0.99{\dot E}_{\mathrm {r}}+\mathrm {j}20{\dot I}_{\mathrm {r}} \\[ 5pt ]
\frac {275}{\sqrt {3}}&=&0.99{\dot E}_{\mathrm {r}}+\mathrm {j}20\times 0 \\[ 5pt ]
0.99{\dot E}_{\mathrm {r}}&=&\frac {275}{\sqrt {3}} \\[ 5pt ]
{\dot E}_{\mathrm {r}}&=&\frac {275}{0.99\sqrt {3}} \\[ 5pt ]
&≒&160 \ \mathrm {[kV]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん