《機械》〈変圧器〉[R07:問2]変圧器の損失の種類と効率に関する空欄穴埋問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，変圧器の損失と効率に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

変圧器の損失には無負荷損と負荷損がある。

無負荷損は，そのほとんどが鉄心で発生する鉄損であり，商用周波数ではその$ \ 80 \ \mathrm {％} \ $程度が$ \ \fbox {　（１）　} \ $損である。また，無負荷損は，一方の巻線を開路し，他方の巻線に定格電圧・定格周波数の電圧を加えたときに消費される有効電力として求められる。

負荷損は，一次及び二次巻線で発生する銅損が主である。負荷電流の増加で増える漏れ磁束によって巻線内部や鉄心押さえ，タンク壁など金属構造物で発生する漂遊負荷損もあるが，非常に小さい。また，負荷損は，一方の巻線を短絡し，他方の巻線に定格周波数の電圧を加えて定格電流を通じたときに消費される有効電力を測定し，指定された$ \ \fbox {　（２）　} \ $巻線温度における値に補正して求められる。

変圧器は回転機に比べて巻線構造が単純であることや，機械損も無いため，効率は非常に高い。いま，定格容量$ \ S_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ $の変圧器がある。その定格電圧における無負荷損は$ \ P_{\mathrm {i}} \ \mathrm {[W]} \ $，定格電流を通じたときの負荷損は$ \ P_{\mathrm {c}} \ \mathrm {[W]} \ $である。力率が$ \ \cos \phi \ $の負荷を二次端子に接続し，この変圧器を負荷率（負荷の容量の変圧器定格容量に対する比）$ \ k \ \left( 0≦k≦1\right) \ $で運転した場合の効率$ \ \eta _{k} \ $は，次式となる。
\[
\begin{eqnarray}
\eta _{k} &=& \frac { \ \fbox {　（３）　} \ }{ \ \fbox {　（３）　} \ +P_{\mathrm {i}}+ \ \fbox {　（４）　} \ }\times 100 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] 上式の効率が最大となる$ \ k \ $は，$ \ k = \ \fbox {　（５）　} \ $である。

〔問1の解答群〕
\[
\begin{eqnarray}
&（イ）&　k^{2}S_{\mathrm {n}}\cos \phi　　　　　&（ロ）&　\sqrt {\frac {P_{\mathrm {i}}}{P_{\mathrm {c}}}}　　　　　&（ハ）&　\frac {P_{\mathrm {c}}}{P_{\mathrm {i}}} \\[ 5pt ] &（ニ）&　ジュール　　　　　&（ホ）&　最高　　　　　&（ヘ）&　\sqrt {\frac {P_{\mathrm {c}}}{P_{\mathrm {i}}}} \\[ 5pt ] &（ト）&　k^{2}P_{\mathrm {c}}　　　　　&（チ）&　kP_{\mathrm {c}}　　　　　&（リ）&　うず電流 \\[ 5pt ] &（ヌ）&　\frac {P_{\mathrm {c}}}{k}　　　　　　　&（ル）&　ヒステリシス　　　　　&（ヲ）&　\left( k\cos \phi \right) ^{2}S_{\mathrm {n}} \\[ 5pt ] &（ワ）&　基準　　　　　&（カ）&　kS_{\mathrm {n}}\cos \phi　　　　　　　&（ヨ）&　理論 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

変圧器の損失と効率に関する問題です。
$ \ 3 \ $種の頃から何度も学習している内容なので，受験生の正答率が高かった問題かと思います。
本問を正答する上では不要ですが，文中に出てくる鉄損や銅損の導出に関する問題も出題されるので，無負荷試験や短絡試験の内容も理解しておいて下さい。

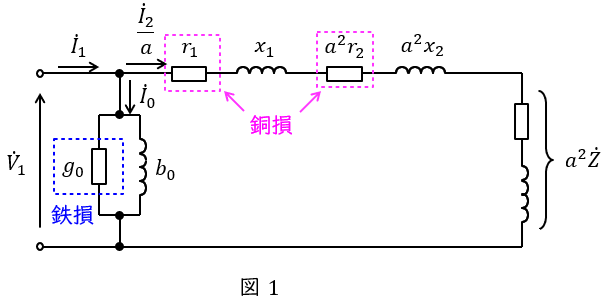
1.変圧器の等価回路（一次換算）と鉄損及び銅損
変圧器の一次側換算等価回路を図1に示します。ただし，$ \ {\dot V}_{1} \ \mathrm {[V]} \ $は一次側端子電圧，$ \ {\dot I}_{1} \ \mathrm {[A]} \ $は一次電流，$ \ {\dot I}_{2} \ \mathrm {[A]} \ $は二次電流，$ \ {\dot I}_{0} \ \mathrm {[A]} \ $は励磁電流，$ \ r_{1} \ \mathrm {[\Omega ]} \ $は一次巻線抵抗，$ \ r_{2} \ \mathrm {[\Omega ]} \ $は二次巻線抵抗，$ \ x_{1} \ \mathrm {[\Omega ]} \ $は一次漏れリアクタンス，$ \ x_{2} \ \mathrm {[\Omega ]} \ $は二次漏れリアクタンス，$ \ g_{0} \ \mathrm {[S]} \ $は励磁コンダクタンス，$ \ b_{0} \ \mathrm {[S]} \ $は励磁サセプタンス，$ \ a \ $は変圧比（巻数比）となります。
等価回路より，鉄損は電圧$ \ {\dot V}_{1} \ $の$ \ 2 \ $乗に比例し，銅損は電流$ \ {\dot I}_{2} \ $の$ \ 2 \ $乗に比例することがわかります。

2.変圧器の効率$ \ \eta \ $と最大効率$ \ \eta _{\mathrm {m}} \ $
変圧器の損失は主に鉄損$ \ p_{\mathrm {i}} \ \mathrm {[W]} \ $と銅損$ \ p_{\mathrm {c}} \ \mathrm {[W]} \ $があり，$ \ p_{\mathrm {i}} \ \mathrm {[W]} \ $は負荷によらず一定であり，$ \ p_{\mathrm {c}} \ \mathrm {[W]} \ $は負荷(電流)の$ \ 2 \ $乗に比例します。従って，定格出力$ \ P_{\mathrm {n}} \ \mathrm {[W]} \ $で利用率$ \ \alpha \ $の時の変圧器の効率$ \ \eta \ $は，
\[
\begin{eqnarray}
\eta &=&\frac {出力}{入力} \\[ 5pt ] &=&\frac {出力}{出力+損失} \\[ 5pt ] &=&\frac {\alpha P_{\mathrm {n}}}{\alpha P_{\mathrm {n}}+p_{\mathrm {i}}+\alpha ^{2}p_{\mathrm {c}}} \\[ 5pt ] \end{eqnarray}
\] となります。
次に，最大効率$ \ \eta _{\mathrm {m}} \ $を求めます。上式の分母分子を$ \ \alpha \ $で割ると
\[
\begin{eqnarray}
\eta &=&\frac {P_{\mathrm {n}}}{\displaystyle P_{\mathrm {n}}+\frac {p_{\mathrm {i}}}{\alpha }+\alpha p_{\mathrm {c}}} \\[ 5pt ] \end{eqnarray}
\] となり，効率が最大となるためには，上式の分母が最小となれば良いです。よって，$ \ \displaystyle A=P_{\mathrm {n}}+\frac {p_{\mathrm {i}}}{\alpha }+\alpha p_{\mathrm {c}} \ $と置くと，
\[
\begin{eqnarray}
\frac {\mathrm {d}A}{\mathrm {d}\alpha }&=&-\frac {p_{\mathrm {i}}}{\alpha ^{2} }+p_{\mathrm {c}} \\[ 5pt ] \end{eqnarray}
\] となります。よって$ \ \displaystyle \frac {\mathrm {d}A}{\mathrm {d}\alpha }=0 \ $となるとき，$ \ p_{\mathrm {i}}=\alpha ^{2}p_{\mathrm {c}} \ $であり，鉄損と銅損が等しい時効率は最大となります。

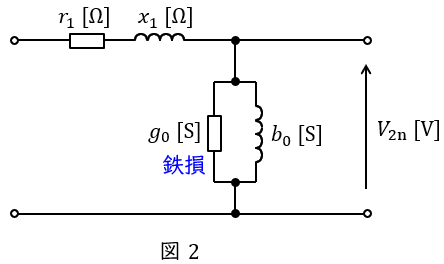
3.無負荷試験の等価回路
変圧器の無負荷試験は一次側を開放して，二次側に定格電圧を加える試験です。測定される電力は鉄損となり，測定される電力と電流から，励磁コンダクタンス$ \ g_{0} \ \mathrm {[S]} \ $及び励磁サセプタンス$ \ b_{0} \ \mathrm {[S]} \ $を求めることが可能となります。二次側に定格電圧を加えるのが一般的ですが，二次側開放で一次側に定格電圧を加えても同様に求められます。

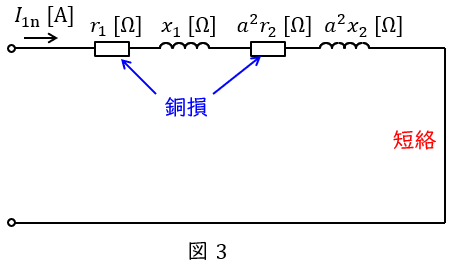
4.短絡試験の等価回路
変圧器の短絡試験は二次側を短絡して，一次側にインピーダンス電圧を加えて，定格電流を流す試験です。励磁回路に流れる電流が十分に小さいと仮定すると，測定される電力は負荷損（銅損）となります。測定される電力と電流から，高圧側換算の巻線抵抗$ \ R=r_{1}+a^{2}r_{2} \ \mathrm {[\Omega ]} \ $及び漏れリアクタンス$ \ X=x_{1}+a^{2}x_{2} \ \mathrm {[\Omega ]} \ $を求めることが可能となります。

5.変圧器の損失
1.無負荷損（鉄損）
1-1．ヒステリシス損$ \ W_{\mathrm {h}} \ $
　交番磁界によって磁性体の磁区の向きが変化します。これに伴って発生する損失をヒステリシス損と言い，鉄損の中で最も大きい損失で以下の式で求められます。
\[
\begin{eqnarray}
W_{\mathrm {h}} &≒& K_{\mathrm {h}}fB_{\mathrm {m}}^{2} \\[ 5pt ] &=& K_{\mathrm {h}}^{\prime }\frac {V^{2}}{f} \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
&&K_{\mathrm {h}}，K_{\mathrm {h}}^{\prime }：比例定数， f：周波数 \\[ 5pt ] &&B_{\mathrm {m}}：最大磁束密度，V：電源電圧 \\[ 5pt ] \end{eqnarray}
\] したがって，$ \ B_{\mathrm {m}} \ $一定の時$ \ W_{\mathrm {h}} \ $は$ \ f \ $に比例し，$ \ V \ $一定の時$ \ W_{\mathrm {h}} \ $は$ \ f \ $に反比例します。

1-2．渦電流損$ \ W_{\mathrm {e}} \ $
　鉄心内で交番磁界の磁束変化が起きると鉄心内に起電力が生じ渦電流が生じます。これに伴って発生する損失を渦電流損と言い，以下の式で求められます。
\[
\begin{eqnarray}
W_{\mathrm {e}} &≒& K_{\mathrm {e}}\left( tfB_{\mathrm {m}}\right) ^{2} \\[ 5pt ] &=& K_{\mathrm {e}}^{\prime }V^{2} \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
&&K_{\mathrm {e}}，K_{\mathrm {e}}^{\prime }：比例定数， f：周波数 \\[ 5pt ] &&B_{\mathrm {m}}：最大磁束密度，V：電源電圧，t：鉄板の厚さ \\[ 5pt ] \end{eqnarray}
\] したがって，$ \ B_{\mathrm {m}} \ $一定の時$ \ W_{\mathrm {h}} \ $は$ \ f \ $の$ \ 2 \ $乗に比例し，$ \ V \ $一定の時$ \ W_{\mathrm {h}} \ $は$ \ f \ $に関係なく一定となります。

2.負荷損
2-1．銅損$ \ W_{\mathrm {c}} \ $
　変圧器の一次巻線及び二次巻線にて生じる抵抗損で，負荷の$ \ 2 \ $乗に比例して増加します。

2-2．漂遊負荷損$ \ W_{\mathrm {s}} \ $
　変圧器での漏れ磁束による損失で，銅損よりかなり小さい値のため，試験ではほぼ無視する場合が多いです。

【解答】

(1)解答：ル
題意より解答候補は，（ニ）ジュール，（リ）うず電流，（ル）ヒステリシス，になると思います。
ワンポイント解説「5.変圧器の損失」の通り，鉄損で最も損失が大きいのはヒステリシス損であり，商用周波数では$ \ 80 \ \mathrm {％} \ $程度となります。

(2)解答：ワ
題意より解答候補は，（ホ）最高，（ワ）基準，（ヨ）理論，になると思います。
負荷損は，一方の巻線を短絡し，他方の巻線に定格周波数の電圧を加えて定格電流を通じたときに消費される有効電力を測定し，基準巻線温度における値（$ \ \mathrm {JEC} \ $において$ \ 75 \ {}^{\circ}\mathrm {C} \ $）に補正して求められます。

(3)解答：カ
題意より解答候補は，（イ）$ \ k^{2}S_{\mathrm {n}}\cos \phi \ $，（ヲ）$ \ \left( k\cos \phi \right) ^{2}S_{\mathrm {n}} \ $，（カ）$ \ kS_{\mathrm {n}}\cos \phi \ $，になると思います。
ワンポイント解説「2.変圧器の効率$ \ \eta \ $と最大効率$ \ \eta _{\mathrm {m}} \ $」の通り，出力は負荷率を考慮した有効電力なので$ \ kS_{\mathrm {n}}\cos \phi \ $となります。

(4)解答：ト
題意より解答候補は，（ト）$ \ k^{2}P_{\mathrm {c}} \ $，（チ）$ \ kP_{\mathrm {c}} \ $，（ヌ）$ \ \displaystyle \frac {P_{\mathrm {c}}}{k} \ $，になると思います。
ワンポイント解説「2.変圧器の効率$ \ \eta \ $と最大効率$ \ \eta _{\mathrm {m}} \ $」の通り，銅損は負荷率の$ \ 2 \ $乗に比例するので$ \ k^{2}P_{\mathrm {c}} \ $となります。

(5)解答：ロ
題意より解答候補は，（ロ）$ \ \displaystyle \sqrt {\frac {P_{\mathrm {i}}}{P_{\mathrm {c}}}} \ $，（ハ）$ \ \displaystyle \frac {P_{\mathrm {c}}}{P_{\mathrm {i}}} \ $，（ヘ）$ \ \displaystyle \sqrt {\frac {P_{\mathrm {c}}}{P_{\mathrm {i}}}} \ $，になると思います。
ワンポイント解説「2.変圧器の効率$ \ \eta \ $と最大効率$ \ \eta _{\mathrm {m}} \ $」の通り，効率が最大となるのは鉄損と銅損が等しいときであるため，
\[
\begin{eqnarray}
P_{\mathrm {i}}&=&k^{2}P_{\mathrm {c}} \\[ 5pt ] k^{2}&=&\frac {P_{\mathrm {i}}}{P_{\mathrm {c}}} \\[ 5pt ] k&=&\sqrt {\frac {P_{\mathrm {i}}}{P_{\mathrm {c}}}} \\[ 5pt ] \end{eqnarray}
\] と求められます。