【問題】
【難易度】★★★☆☆(普通)
次の文章は,整流回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。なお,すべての回路素子は理想的であり,ダイオードの電圧降下などは無視するものとする。また,選択肢の波形については,縦軸のスケールは,それぞれ異なっている。
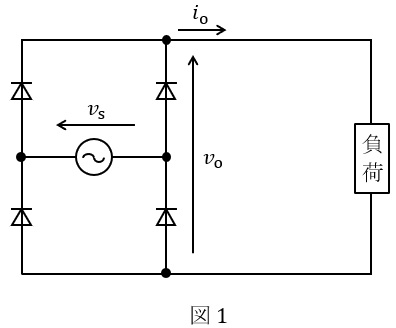
冷蔵庫やエアコンを始めとする家電製品の多くには,交流から直流への電力変換回路である単相整流回路が組み込まれている。単相整流回路の一つに,図1に示すダイオードを\( \ 4 \ \)個使用した単相ダイオードブリッジ整流回路がある。
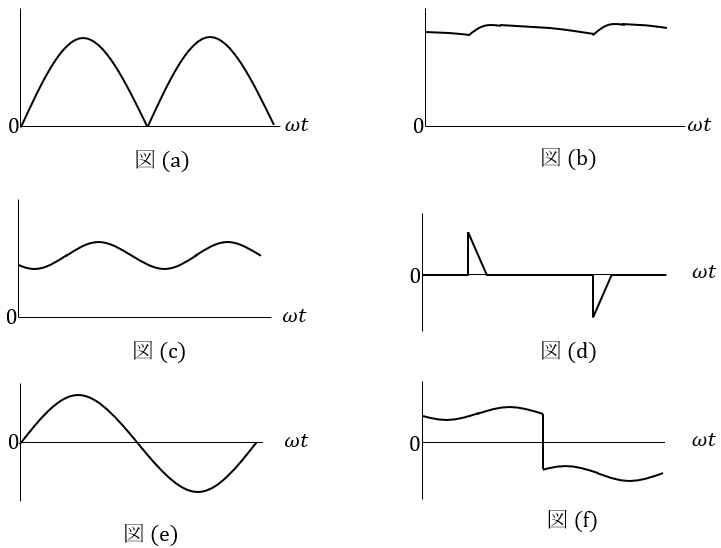
単相ダイオードブリッジ整流回路の直流出力に負荷として抵抗を接続し,交流入力に電圧が\( \ v_{\mathrm {s}}=\sqrt {2}V\sin \omega t \ \mathrm {[V]} \ \)で表される交流電源を接続したときに,電圧\( \ v_{\mathrm {o}} \ \)の波形は図\( \ \fbox { (1) } \ \)のようになる。このとき電圧\( \ v_{\mathrm {o}} \ \)の直流成分は\( \ \fbox { (2) } \ \mathrm {[V]} \ \)となる。
ダイオードブリッジ整流回路の出力電圧\( \ v_{\mathrm {o}} \ \)や電流\( \ i_{\mathrm {o}} \ \)を平滑化(脈動を抑制)する方法には,次の\( \ 2 \ \)種類がある。一つはコンデンサをダイオードブリッジ整流回路の直流出力に\( \ \fbox { (3) } \ \)接続することで電圧\( \ v_{\mathrm {o}} \ \)を平滑化するコンデンサインプット形整流回路である。もう一つはチョークコイルをダイオードブリッジ整流回路の直流出力に\( \ \fbox { (4) } \ \)接続することで電流\( \ i_{\mathrm {o}} \ \)を平滑化するチョークインプット形整流回路である。
コンデンサインプット形整流回路の場合,交流電源に流れる電流波形は図\( \ \fbox { (5) } \ \)のようになり,チョークインプット形整流回路の場合,交流電源に流れる電流波形は図\( \ \fbox { (6) } \ \)のようになる。また両者を比べると,チョークコイルのインダクタンスもしくはコンデンサの静電容量が十分大きい場合には,電源の総合力率は,\( \ \fbox { (7) } \ \)形整流回路の方が高くなる。
〔問5の解答群〕
\[
\begin{eqnarray}
&(イ)& \mathrm {(a)} &(ロ)& \mathrm {(b)} &(ハ)& \mathrm {(c)} \\[ 5pt ]
&(ニ)& \mathrm {(d)} &(ホ)& \mathrm {(e)} &(ヘ)& \mathrm {(f)} \\[ 5pt ]
&(ト)& \frac {\sqrt {2}}{2}V &(チ)& \frac {\sqrt {2}}{\pi }V &(リ)& \mathrm {Y} \\[ 5pt ]
&(ヌ)& \mathrm {\Delta } &(ル)& 直列 &(ヲ)& \frac {2\sqrt {2}}{\pi }V \\[ 5pt ]
&(ワ)& チョークインプット &(カ)& コンデンサインプット &(ヨ)& 並列 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
単相ダイオード整流回路の波形と動作原理に関する問題です。
しっかりと理解していればそれほど難易度が高い内容ではありませんが,パワーエレクトロニクスは不得手としている受験生も多いため,正答率はそれほど高くなかったことが予想されます。
まずは動作原理をしっかりと理解して解いていくようにして下さい。
1.単相ダイオードブリッジ整流回路の動作
図2-1及び図2-2に示す単相ダイオードブリッジ整流回路は以下のように動作します。
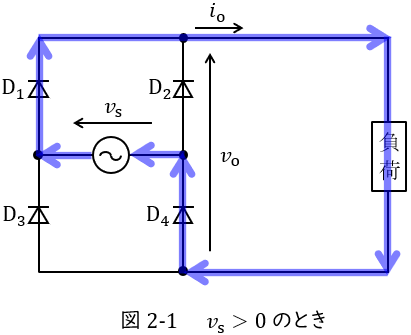
①\( \ v_{\mathrm {s}}>0 \ \)のとき
図2-1のように,電流は交流電源→\( \ \mathrm {D}_{1} \ \)→負荷→\( \ \mathrm {D}_{4} \ \)→交流電源と流れます。出力電圧\( \ v_{\mathrm {o}} \ \)は素子の電圧降下が無視できるとすると,入力電圧\( \ v_{\mathrm {s}} \ \)と等しくなります。
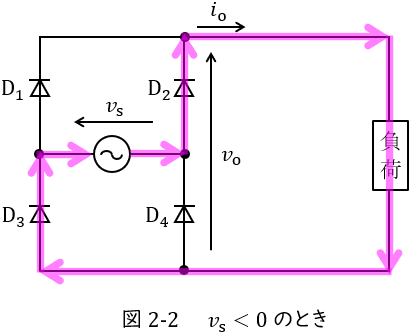
②\( \ v_{\mathrm {s}}<0 \ \)のとき
図2-2のように,電流は交流電源→\( \ \mathrm {D}_{2} \ \)→負荷→\( \ \mathrm {D}_{3} \ \)→交流電源と流れます。出力電圧\( \ v_{\mathrm {o}} \ \)は素子の電圧降下が無視できるとすると,\( \ -v_{\mathrm {s}} \ \)となります。
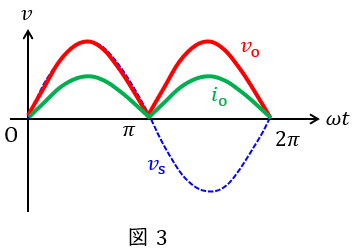
したがって,抵抗負荷を接続したときの出力電圧及び電流の波形は図3のようになります。
図3より平均出力電圧\( \ V_{\mathrm {o}} \ \mathrm {[V]} \ \)は,交流入力\( \ v=\sqrt {2}V \sin \omega t \ \mathrm {[V]} \ \)とすると,
\[
\begin{eqnarray}
V_{\mathrm {o}} &=& \frac {1}{\pi }\int _{0}^{\pi }\sqrt {2}V\sin \omega t \mathrm {d}\omega t \\[ 5pt ]
&=& \frac {\sqrt {2}}{\pi }V\left[ -\cos \omega t\right] _{0}^{\pi } \\[ 5pt ]
&=& \frac {\sqrt {2}}{\pi }V\left( -\cos \pi +\cos 0 \right) \\[ 5pt ]
&=& \frac {\sqrt {2}}{\pi }V\left\{ -\left( -1 \right) +1 \right\} \\[ 5pt ]
&=& \frac {2\sqrt {2}}{\pi }V \\[ 5pt ]
&≃& 0.90V \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.コンデンサとリアクトルの平滑作用
整流回路の出力電圧や電流は波形の脈動が多いため,コンデンサやリアクトルを挿入し平滑させることがあります。
①コンデンサ
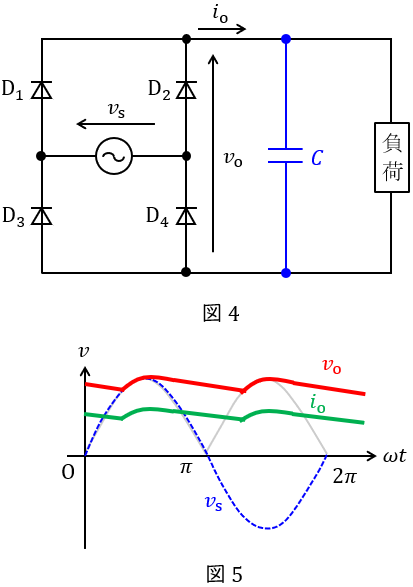
図4の示すように,負荷に並列にコンデンサを挿入することで,コンデンサの充放電により電圧波形の脈動が平滑されます。これにより,図5に示すような波形の出力が得られることになります。
②リアクトル
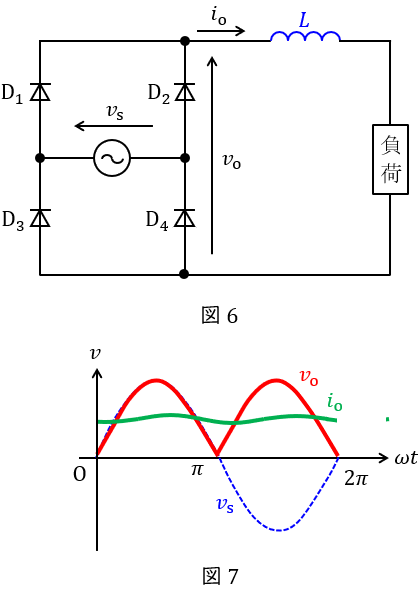
図6に示すように,負荷に直列にリアクトルを挿入することで,リアクトルの作用により電流波形の脈動が平滑されます。これにより,図7に示すような波形の出力が得られることになります。
【解答】
(1)解答:イ
題意より解答候補は,(イ)\( \ \mathrm {(a)} \ \),(ロ)\( \ \mathrm {(b)} \ \),(ハ)\( \ \mathrm {(c)} \ \),(ニ)\( \ \mathrm {(d)} \ \),(ホ)\( \ \mathrm {(e)} \ \),(ヘ)\( \ \mathrm {(f)} \ \),になると思います。
ワンポイント解説「1.単相ダイオードブリッジ整流回路の動作」図3の通り,電圧\( \ v_{\mathrm {o}} \ \)の波形は図\( \ \mathrm {(a)} \ \)のようになります。
(2)解答:ヲ
題意より解答候補は,(ト)\( \ \displaystyle \frac {\sqrt {2}}{2}V \ \),(チ)\( \ \displaystyle \frac {\sqrt {2}}{\pi }V \ \),(ヲ)\( \ \displaystyle \frac {2\sqrt {2}}{\pi }V \ \),になると思います。
ワンポイント解説「1.単相ダイオードブリッジ整流回路の動作」の通り,電圧\( \ v_{\mathrm {o}} \ \)の電圧は\( \ \displaystyle \frac {2\sqrt {2}}{\pi }V \ \mathrm {[V]} \ \)となります。
(3)解答:ヨ
題意より解答候補は,(リ)\( \ \mathrm {Y} \ \),(ヌ)\( \ \mathrm {\Delta } \ \),(ル)直列,(ヨ)並列,になると思います。
ワンポイント解説「2.コンデンサとリアクトルの平滑作用」の通り,コンデンサインプット形整流回路はコンデンサをダイオードブリッジ整流回路の直流出力に並列に接続します。
(4)解答:ル
題意より解答候補は,(リ)\( \ \mathrm {Y} \ \),(ヌ)\( \ \mathrm {\Delta } \ \),(ル)直列,(ヨ)並列,になると思います。
ワンポイント解説「2.コンデンサとリアクトルの平滑作用」の通り,チョークインプット形整流回路はチョークコイルをダイオードブリッジ整流回路の直流出力に直列に接続します。
(5)解答:ニ
題意より解答候補は,(イ)\( \ \mathrm {(a)} \ \),(ロ)\( \ \mathrm {(b)} \ \),(ハ)\( \ \mathrm {(c)} \ \),(ニ)\( \ \mathrm {(d)} \ \),(ホ)\( \ \mathrm {(e)} \ \),(ヘ)\( \ \mathrm {(f)} \ \),になると思います。
ワンポイント解説「2.コンデンサとリアクトルの平滑作用」の通り,コンデンサを挿入している場合,電源電圧よりコンデンサ電圧が高い状態が維持できている間はコンデンサから電荷が放出され電源には電流が流れず,入力電圧のピーク付近で電流が流れることになるので,電流波形は図\( \ \mathrm {(d)} \ \)のようになります。
(6)解答:ヘ
題意より解答候補は,(イ)\( \ \mathrm {(a)} \ \),(ロ)\( \ \mathrm {(b)} \ \),(ハ)\( \ \mathrm {(c)} \ \),(ニ)\( \ \mathrm {(d)} \ \),(ホ)\( \ \mathrm {(e)} \ \),(ヘ)\( \ \mathrm {(f)} \ \),になると思います。
ワンポイント解説「2.コンデンサとリアクトルの平滑作用」の通り,リアクトルを挿入している場合,負荷の電流はあまり上下せず図\( \ \mathrm {(c)} \ \)のように流れます。交流電源は同じ電流値が流れますが,正負が切り替わるタイミングで電流の向きが変わるため,電流波形として適当なのは図\( \ \mathrm {(f)} \ \)となります。
(7)解答:ワ
題意より解答候補は,(ワ)チョークインプット,(カ)コンデンサインプット,になると思います。
図\( \ \mathrm {(d)} \ \)と図\( \ \mathrm {(f)} \ \)を比較すると,図\( \ \mathrm {(d)} \ \)の方が力率が悪いことが読み取れます。したがって,電源の総合力率は,チョークインプット形整流回路の方が高くなります。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん