《機械》〈回転機〉[R01:問1]容量性負荷における同期発電機の特性に関する空欄穴埋問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，容量性負荷における同期発電機の特性に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

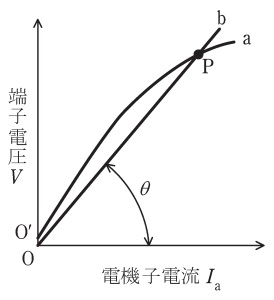
無負荷の長距離送電線に同期発電機を無励磁で接続しても，送電線の線間及び対地静電容量の影響によってこれらを充電する電機子電流が流れ，これによって発電機の端子電圧が高められ，さらに電流が増すという過程を繰り返して，端子電圧が著しく増大することがある。このときの同期発電機の電機子電流$ \ I_{\mathrm {a}} \ $に対する端子電圧$ \ V \ $は図の曲線$ \ \mathrm {O^{\prime }a} \ $のような飽和特性であるとする。同期発電機に上述の静電容量に相当する$ \ 1 \ $相当たりキャパシタンス$ \ C \ $の容量性負荷を接続した場合，その電圧電流特性を直線$ \ \mathrm {Ob} \ $で表し，その傾きを$ \ \tan \theta \ $とする。発電機には残留磁気による誘導起電力$ \ \mathrm {OO^{\prime }} \ $を生じているから，これによって$ \ \fbox {　（１）　} \ $の電機子電流が流れる。この電流による電機子反作用は$ \ \fbox {　（２）　} \ $作用となり端子電圧を上昇させ，ある電機子電流$ \ I_{\mathrm {a}} \ $に対して飽和曲線$ \ \mathrm {O^{\prime }a} \ $の方が直線$ \ \mathrm {Ob} \ $よりも大きい間は電圧及び電流ともに増加し続け，曲線$ \ \mathrm {O^{\prime }a} \ $と直線$ \ \mathrm {Ob} \ $の交点$ \ \mathrm {P} \ $に達し，この点で安定し運転を持続する。このような現象を同期発電機の$ \ \fbox {　（３）　} \ $といい，点$ \ \mathrm {P} \ $を$ \ \fbox {　（４）　} \ $点という。点$ \ \mathrm {P} \ $の電圧はキャパシタンス$ \ C \ $の大きさによって上下する。$ \ C \ $が$ \ \fbox {　（５）　} \ $く，傾き$ \ \tan \theta \ $が小さい場合，点$ \ \mathrm {P} \ $の電圧が高くなる。その結果，点$ \ \mathrm {P} \ $の電圧が発電機の定格電圧より非常に高くなる場合には，機器の絶縁を脅かすことになる。これを防ぐためには，その交点の電圧が同期発電機の定格電圧よりも低いことが必要である。

〔問1の解答群〕
\[
\begin{eqnarray}
&（イ）&　自動励磁　　　　　&（ロ）&　同相　　　　　&（ハ）&　減磁 \\[ 5pt ] &（ニ）&　運転継続　　　　　&（ホ）&　電圧確立　　　　　&（ヘ）&　大き \\[ 5pt ] &（ト）&　交差磁化　　　　　&（チ）&　自動電圧調整　　　　　&（リ）&　増磁 \\[ 5pt ] &（ヌ）&　進相　　　　　&（ル）&　励磁可能　　　　　&（ヲ）&　小さ \\[ 5pt ] &（ワ）&　自己励磁　　　　　&（カ）&　遅相　　　　　&（ヨ）&　同期化 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

自己励磁現象のメカニズムそのものといった出題内容です。ほとんどの方は2種時代にも勉強されているとは思いますが，非常に重要な内容なのでこの問題で再度学習されると良いと思います。

1.自己励磁現象
自己励磁現象は図1に示すように，系統が対地静電容量によって容量性負荷である時に電機子反作用が増磁作用に働くために発生する現象です。メカニズムは以下の通りです。
①　残留磁気の影響で発電機の誘導起電力が上昇する。
②　系統は容量性なので進み電流が流れる。
③　電機子反作用により増磁作用となる。
④　発電機の誘導起電力が上昇する。
以後②～④を繰り返す。

【解答】

(1)解答：ヌ
題意より，解答候補は（ロ）同相，（ヌ）進相，（カ）遅相，となると思います。容量性負荷を接続した場合は進相の電機子電流が流れます。

(2)解答：リ
題意より，解答候補は（ハ）減磁，（ト）交差磁化，（リ）増磁，となると思います。減磁作用は誘導性負荷のとき，交差磁化作用は力率が1の時，増磁作用は容量性負荷の時に働く電機子反作用です。

(3)解答：ワ
題意より，解答候補は（イ）自動励磁，（ニ）運転継続，（ホ）電圧確立，（ワ）自己励磁，（ヨ）同期化，等となると思います。ワンポイント解説「1.自己励磁現象」の通り，本問の現象を自己励磁現象と呼びます。

(4)解答：ホ
題意より，解答候補は（イ）自動励磁，（ニ）運転継続，（ホ）電圧確立，（ワ）自己励磁，（ヨ）同期化，等となると思います。少しマニアックな名称ですが点$ \ \mathrm {P} \ $を電圧確立点と呼びます。

(5)解答：ヘ
題意より，解答候補は（ヘ）大き，（ヲ）小さ，になると思います。容量性負荷である時，系統の電圧と電流の関係は$ \ \displaystyle V = \frac {1}{2\pi f C}I \ $の関係があるので，$ \ C \ $が大きくなるほど直線$ \ \mathrm {Ob} \ $の傾きが小さくなるので，交点$ \ \mathrm {P} \ $が上昇します。