【問題】
【難易度】★☆☆☆☆(易しい)
定格出力\( \ 3.7 \ \mathrm {kW} \ \),定格電圧\( \ 200 \ \mathrm {V} \ \),定格周波数\( \ 50 \ \mathrm {Hz} \ \)の\( \ 4 \ \)極かご形三相誘導電動機がある。この電動機に関して,次の問に答えよ。ただし,星形一相の\( \ \mathrm {L} \ \)型等価回路において励磁回路は無視し,抵抗値\( \ [\Omega ] \ \)及びリアクタンス値\( \ [\Omega ] \ \)は次のとおりとする。なお,機械損は無視するものとする。
一次抵抗\( \ r_{1}=0.33 \ \Omega \ \),一次漏れリアクタンス\( \ x_{1}=0.63 \ \Omega \ \)
二次抵抗\( \ r_{2}^{\prime }=0.33 \ \Omega \ \),二次漏れリアクタンス\( \ x_{2}^{\prime }=0.63 \ \Omega \ \)
ここで,\( \ r_{2}^{\prime } \ \),\( \ x_{2}^{\prime } \ \)はいずれも一次換算値である。
(1) 定格電圧,滑り\( \ 3 \ \mathrm {%} \ \)で運転しているときの一次換算二次電流\( \ \mathrm {[A]} \ \)を求めよ。
(2) そのときの出力\( \ \mathrm {[kW]} \ \)を求めよ。
(3) そのときのトルク\( \ \mathrm {[N\cdot m]} \ \)を求めよ。
(4) この電動機の端子電圧を定格の\( \ 80 \ \mathrm {%} \ \)に下げた場合に,上記(3)で得られたトルクと同一トルクが発生しているときの滑り\( \ \mathrm {[%]} \ \)を求めよ。
【ワンポイント解説】
かご形三相誘導電動機の出力やトルクの特性に関する問題です。
(4)の計算を丁寧に解いていく必要がありますが,解法自体は非常に易しいため,試験後「\( \ 1 \ \)種の問題としては易しすぎる」と話題になった問題です。
本問のような問題を選択し,確実に完答することが合格への近道となります。
1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)及び同期角速度\( \ \omega _{\mathrm {s}} \ \)
三相誘導電動機の極数が\( \ p \ \),電源の周波数が\( \ f \ \mathrm {[Hz]} \ \)の時,同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)は,
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ]
\end{eqnarray}
\]
となります。また,同期角速度\( \ \omega _{\mathrm {s}} \ \mathrm {[rad / s]} \ \)は,
\[
\begin{eqnarray}
\omega _{\mathrm {s}} &=&\frac {2\pi N_{\mathrm {s}}}{60} \\[ 5pt ]
&=&\frac {2\pi }{60}\cdot \frac {120f}{p} \\[ 5pt ]
&=&\frac {4\pi f}{p} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
2.誘導機の滑り\( \ s \ \)
誘導機の同期速度が\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \),回転子の回転速度が\( \ N \ \mathrm {[{min}^{-1}]} \ \)である時,誘導機の滑り\( \ s \ \)は,
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
と定義されます。これを整理すると,
\[
\begin{eqnarray}
sN_{\mathrm {s}} &=&N_{\mathrm {s}}-N \\[ 5pt ]
N &=&N_{\mathrm {s}}-sN_{\mathrm {s}} \\[ 5pt ]
&=&\left( 1-s \right) N_{\mathrm {s}} \\[ 5pt ]
\end{eqnarray}
\]
と同期速度から回転速度が導出できます。
3.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係
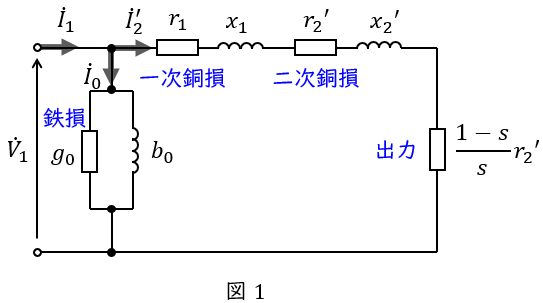
誘導電動機の\( \ \mathrm {L} \ \)形等価回路は図1のようになります。図1において,\( \ {\dot V}_{1} \ \mathrm {[V]} \ \)は一次側端子電圧,\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は一次電流,\( \ {\dot I}_{2}^{\prime } \ \mathrm {[A]} \ \)は二次電流の一次換算,\( \ {\dot I}_{0} \ \mathrm {[A]} \ \)は励磁電流,\( \ r_{1} \ \mathrm {[\Omega ]} \ \)は一次巻線抵抗,\( \ r_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次巻線抵抗の一次換算,\( \ x_{1} \ \mathrm {[\Omega ]} \ \)は一次漏れリアクタンス,\( \ x_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次漏れリアクタンスの一次換算,\( \ s \ \)は滑りとなります。
図1より,出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \),二次銅損\( \ P_{\mathrm {c2}} \ \mathrm {[W]} \ \),二次入力\( \ P_{2} \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {o}} &=& 3\frac {1-s}{s}r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ]
P_{\mathrm {c2}} &=& 3r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ]
P_{2} &=& P_{\mathrm {o}}+P_{\mathrm {c2}} =3\frac {r_{2}^{\prime }}{s}{I_{2}^{\prime }}^{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,誘導電動機の二次入力\( \ P_{2} \ \mathrm {[W]} \ \),出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \),二次銅損\( \ P_{\mathrm {c2}} \ \mathrm {[W]} \ \)には,
\[
\begin{eqnarray}
P_{2}:P_{\mathrm {o}}:P_{\mathrm {c2}} &=& 1:(1-s):s \\[ 5pt ]
\end{eqnarray}
\]
の関係があることが分かります。
4.誘導電動機のトルク
図1より,三相誘導電動機のトルク\( \ T \ \mathrm {[N\cdot m]} \ \)は,
\[
\begin{eqnarray}
T &=&\frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ]
&=&\frac {P_{\mathrm {2}}\left( 1-s\right) }{\omega _{\mathrm {s}}\left( 1-s\right) } \\[ 5pt ]
&=&\frac {P_{\mathrm {2}}}{\omega _{\mathrm {s}}} \\[ 5pt ]
&=& \frac {1}{\omega _{\mathrm {s}}}\frac {3V_{1}^{2}\displaystyle \frac {r_{2}^{\prime }}{s}}{\left( r_{1}+\displaystyle \frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
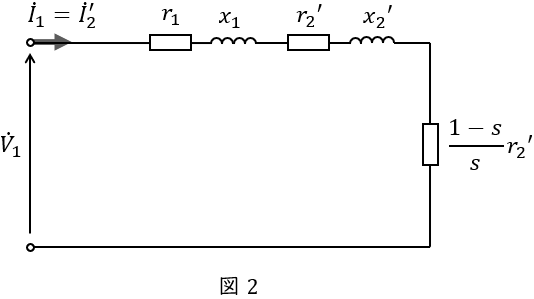
(1)定格電圧,滑り\( \ 3 \ \mathrm {%} \ \)で運転しているときの一次換算二次電流\( \ \mathrm {[A]} \ \)
励磁回路は無視できるので\( \ \mathrm {L} \ \)型等価回路は図2のようになる。等価回路より,一次換算二次電流\( \ I_{2}^{\prime } \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{2}^{\prime } &=&\frac {V_{1}}{\sqrt {\left( r_{1}+\displaystyle \frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,各値を代入して計算すると,
\[
\begin{eqnarray}
I_{2}^{\prime } &=&\frac {\displaystyle \frac {200}{\sqrt {3}}}{\sqrt {\left( 0.33+\displaystyle \frac {0.33}{0.03}\right) ^{2}+\left( 0.63+0.63\right) ^{2}}} \\[ 5pt ]
&≒&10.129 → 10.1 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)(1)と同条件における出力\( \ \mathrm {[kW]} \ \)
(1)と同条件における出力\( \ P \ \mathrm {[kW]} \ \)は,ワンポイント解説「3.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係」の通り,
\[
\begin{eqnarray}
P_{\mathrm {o}} &=& 3\frac {1-s}{s}r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ]
&=& 3\times \frac {1-0.03}{0.03}\times 0.33\times 10.129^{2} \\[ 5pt ]
&≒& 3 \ 284.1 \ \mathrm {[W]} → 3.28 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)(1)と同条件におけるトルク\( \ \mathrm {[N\cdot m]} \ \)
定格周波数\( \ f=50 \ \mathrm {[Hz]} \ \),極数\( \ p=4 \ \)より,同期角速度\( \ \omega _{\mathrm {s}} \ \mathrm {[rad / s]} \ \)は,ワンポイント解説「1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)及び同期角速度\( \ \omega _{\mathrm {s}} \ \)」の通り,
\[
\begin{eqnarray}
\omega _{\mathrm {s}} &=&\frac {4\pi f}{p} \\[ 5pt ]
&=&\frac {4\pi \times 50}{4} \\[ 5pt ]
&≒&157.08 \ \mathrm {[rad / s]} \\[ 5pt ]
\end{eqnarray}
\]
となり,滑り\( \ s=0.03 \ \)のときの角速度\( \ \omega \ \mathrm {[rad / s]} \ \)は,
\[
\begin{eqnarray}
\omega &=&\omega _{\mathrm {s}} \left( 1-s\right) \\[ 5pt ]
&=&157.08\times \left( 1-0.03\right) \\[ 5pt ]
&≒&152.37 \ \mathrm {[rad / s]} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,トルク\( \ T \ \mathrm {[N\cdot m]} \ \)は,ワンポイント解説「4.誘導電動機のトルク」の通り,
\[
\begin{eqnarray}
T &=&\frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ]
&=&\frac {3 \ 284.1}{152.37} \\[ 5pt ]
&≒&21.553 → 21.6 \ \mathrm {[rad / s]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)端子電圧を定格の\( \ 80 \ \mathrm {%} \ \)に下げた場合の(3)で得られたトルクと同一トルクが発生しているときの滑り\( \ \mathrm {[%]} \ \)
ワンポイント解説「4.誘導電動機のトルク」の通り,二次入力\( \ P_{2} \ \mathrm {[W]} \ \)とすると,
\[
\begin{eqnarray}
T &=&\frac {P_{\mathrm {2}}}{\omega _{\mathrm {s}}} \\[ 5pt ]
&=&\frac {\displaystyle 3\frac {r_{2}^{\prime }}{s}{I_{2}^{\prime }}^{2}}{\omega _{\mathrm {s}}} \\[ 5pt ]
&=&\frac {1}{\omega _{\mathrm {s}}}\frac {3V_{1}^{2}\displaystyle \frac {r_{2}^{\prime }}{s}}{\left( r_{1}+\displaystyle \frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
の関係があり,題意より端子電圧を\( \ 80 \ \mathrm {%} \ \)に下げた場合にも同一トルクが発生しているので,そのときの滑りを\( \ s^{\prime } \ \)とすると,
\[
\begin{eqnarray}
T&=&\frac {1}{\omega _{\mathrm {s}}}\frac {3\times \left( 0.8V_{1}\right) ^{2}\displaystyle \frac {r_{2}^{\prime }}{s^{\prime }}}{\left( r_{1}+\displaystyle \frac {r_{2}^{\prime }}{s^{\prime }}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
が成立する。これに各値を代入して整理していくと,
\[
\begin{eqnarray}
21.553&=&\frac {1}{157.08}\times \frac {\displaystyle 3\times \left( 0.8\times \frac {200}{\sqrt {3}}\right) ^{2}\times \frac {0.33}{s^{\prime }}}{\left( 0.33+\displaystyle \frac {0.33}{s^{\prime }}\right) ^{2}+\left( 0.63+0.63\right) ^{2}} \\[ 5pt ]
21.553\times 157.08&=& \frac {\displaystyle \frac {8 \ 448}{s^{\prime }}}{\displaystyle 0.108 \ 9+\frac {0.217 \ 8}{s^{\prime }}+\frac {0.108 \ 9}{{s^{\prime }}^{2}}+1.587 \ 6} \\[ 5pt ]
&=& \frac {8 \ 448s^{\prime }}{1.696 \ 5{s^{\prime }}^{2}+0.217 \ 8s^{\prime }+0.108 \ 9} \\[ 5pt ]
1.696 \ 5{s^{\prime }}^{2}+0.217 \ 8s^{\prime }+0.108 \ 9&=& \frac {8 \ 448s^{\prime }}{21.553\times 157.08} \\[ 5pt ]
&≒& 2.495 \ 3s^{\prime } \\[ 5pt ]
1.696 \ 5{s^{\prime }}^{2}-2.277 \ 5s^{\prime }+0.108 \ 9&≒&0 \\[ 5pt ]
{s^{\prime }}^{2}-1.342 \ 5s^{\prime }+0.064 \ 191&≒&0 \\[ 5pt ]
s^{\prime }&=&\frac {1.342 \ 5±\sqrt {1.342 \ 5^{2}-4\times 1\times 0.064 \ 191}}{2} \\[ 5pt ]
&≒&0.049 \ 7 , \color {red}{1.29 \ \left( 不適\right) } \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ 4.97 \ \mathrm {%} \ \)と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん