《機械》〈照明〉[H26:問6]乳白ガラス球を用いた照明器具に関する計算・空欄穴埋問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，乳白ガラス球を用いた照明器具の照明計算に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。なお，$ \ \pi \ $は$ \ 3.1416 \ $とする。

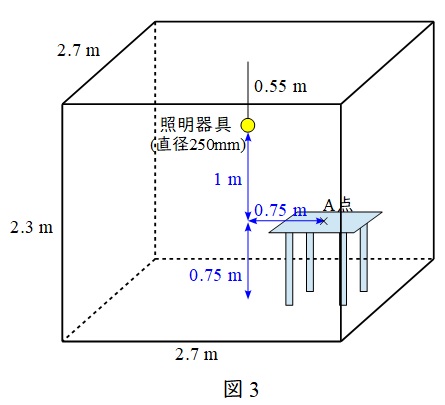
直径$ \ 250 \ \mathrm {mm} \ $の乳白ガラスの照明器具が，奥行き$ \ 2.7 \ \mathrm {m} \times $間口$ \ 2.7 \ \mathrm {m} \ $，天井高さ$ \ 2.3 \ \mathrm {m} \ $の室内の天井中央から，照明器具中心まで$ \ 0.55 \ \mathrm {m} \ $の長さでつるされている。照明器具内部には全光束$ \ \phi =810 \ \mathrm {lm} \ $のランプがあり，乳白ガラスで光が均等に拡散し$ \ 1067 \ \mathrm {cd / m^{2}} \ $で輝いている。このような設定において，以下の三つの問題を考える。なお，乳白ガラス内面の反射率$ \ \rho = 20 \ ％ \ $，透過率$ \ \tau =65 \ ％ \ $，残りはガラスで吸収され，ガラスの厚みは無視できるものとする。また，室内各面等での相互反射は無視できるものとする。

a.照明器具直下から水平に$ \ 0.75 \ \mathrm {m} \ $離れた机上面$ \ \mathrm {A} \ $点(床上$ \ 0.75 \ \mathrm {m} \ $ )の水平面照度を求める。

照明器具が$ \ 1067 \ \mathrm {cd / m^{2}} \ $で均等に輝いているので，$ \ \mathrm {A} \ $点方向の光度は約$ \ \fbox {　（１）　} \ \mathrm {cd} \ $である。照明器具と$ \ \mathrm {A} \ $点との距離は，照明器具の直径より十分大きいので，照明器具を点とみなして机上面$ \ \mathrm {A} \ $点の水平面照度を計算すると$ \ \fbox {　（２）　} \ \mathrm {lx} \ $となる。

b.次に，机など障害物がない場合の室全体の平均照度を求める。

光束は，光度と$ \ \fbox {　（３）　} \ $の積である。また，$ \ \fbox {　（３）　} \ $は，光中心から半径$1$の単位球上にある面を仮定したときのその表面積でもある。この関係から照明器具の全光束が求まるので，室空間全体の平均照度は$ \ \fbox {　（４）　} \ \mathrm {lx} \ $となる。

c.照明器具内の相互反射による光束が，照明器具の全光束に占める割合を求める。

照明器具の全光束は，ランプ全光束の直接透過成分に照明器具内部での相互反射成分が加わった値である。相互反射による内面の間接照度$ \ E_{\mathrm {i}} \ $は，球内の表面積を$ \ S \ $としたときに次式で求めることができる。
\[
\begin{eqnarray}
E_{\mathrm {i}}&=& \frac {\phi }{S}\times \frac {\rho }{\left( 1-\rho \right) } \\[ 5pt ] \end{eqnarray}
\] 照明器具内の相互反射による光束は，照明器具の全光束の$ \ \fbox {　（５）　} \ ％ \ $を占める。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　41.9　　　　　&（ロ）&　立体角　　　　　&（ハ）&　20.0 \\[ 5pt ] &（ニ）&　10.0　　　　　&（ホ）&　15.0　　　　　&（ヘ）&　84.9 \\[ 5pt ] &（ト）&　52.4　　　　　&（チ）&　43.5　　　　　&（リ）&　26.8 \\[ 5pt ] &（ヌ）&　正射影面積　　　　　&（ル）&　21.5　　　　　&（ヲ）&　66.8 \\[ 5pt ] &（ワ）&　13.4　　　　　&（カ）&　16.7　　　　　&（ヨ）&　照明器具の見かけの大きさ \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

三種の頃からよく出題されている公式を使用する問題です。一種で照明が出題されると配点が高いので，確実な得点源となる様準備しておきましょう。

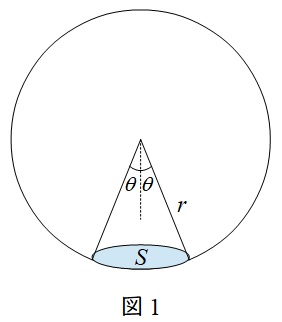
1.立体角の定義
図1のように球体があり，半径$ \ r \ \mathrm {[m]} \ $の錐体が球面を切り取った時の面積を$ \ S \ \mathrm {[m^{2}]} \ $とすると，立体角$ \ \omega \ \mathrm {[sr]} \ $は，
\[
\begin{eqnarray}
\omega &=&\frac {S}{r^{2}} \\[ 5pt ] \end{eqnarray}
\] であり，平面角$ \ \theta \ \mathrm {[rad]} \ $で表すと，
\[
\begin{eqnarray}
\omega &=&2\pi \left( 1-\cos \theta \right) \\[ 5pt ] \end{eqnarray}
\] となります。球全体の立体角は$ \ \theta = \pi \ $であり，$ \ \omega =4\pi \ $となります。

2.光束$ \ \mathit {\Phi } \ $
光の量で単位はルーメン$ \ \mathrm {[lm]} \ $となります。電磁気で言うと磁束のようなものです。

3.光度$ \ I \ $
光束を立体角で割ったものです。微小立体角$ \ \Delta \omega \ $に含まれる光束を$ \ \mathit {\Phi } \ $とすると，光度$ \ I \ $は，
\[
I= \frac {\mathit {\Phi }}{\Delta \omega}　\mathrm {[cd]}
\] となります。

4.照度$ \ E \ $
均一に照射された面の明るさで，微小面積$ \ \Delta A \ $に入射する光束を$ \ \mathit {\Phi } \ $とすると，
\[
E=\frac {\mathit {\Phi }}{\Delta A}\mathrm {[lx]}
\] となります。

5.輝度$ \ L \ $
物の眩しさを表す指標で，ある方向の光度$ \ I \ $，見かけの面積$ \ S \ $とすると，
\[
L=\frac {I}{S}\mathrm {[cd / m^{2}]}
\] となります。

6.逆$ \ 2 \ $乗の法則
照度の定義式$ \ \displaystyle E=\frac {\mathit {\Phi }}{\Delta A} \ $に光度の定義式$ \ \displaystyle I= \frac {\mathit {\Phi }}{\Delta \omega} \ $と立体角の定義$ \ \Delta A=\Delta \omega r^{2} \ $を代入すると，
\[
E=\frac {\mathit {\Phi }}{\Delta A}=\frac {I\Delta \omega}{\Delta \omega r^{2}}=\frac {I}{r^{2}}
\] となります。

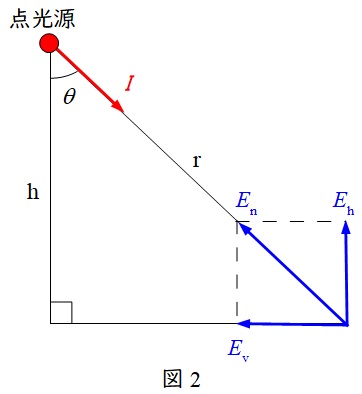
7.水平面照度と鉛直面照度
図2における$ \ E_{\mathrm {n}} \ $を法線照度，$ \ E_{\mathrm {h}} \ $を水平面照度，$ \ E_{\mathrm {v}} \ $を鉛直面照度と言い，以下のような関係があります。
\[
\begin{eqnarray}
E_{\mathrm {n}}&=&\frac {I}{r^{2}}&=&\frac {I\cdot \cos^{2}\theta }{h^{2}} \\[ 5pt ] E_{\mathrm {h}}&=&E_{\mathrm {n}}\cos\theta &=&\frac {I\cdot \cos^{3}\theta }{h^{2}} \\[ 5pt ] E_{\mathrm {v}}&=&E_{\mathrm {n}}\sin\theta &=&\frac {I\cdot \sin\theta \cos^{2}\theta }{h^{2}} \\[ 5pt ] \end{eqnarray}
\]

【解答】

(1)解答：ト
a.の題意に沿って図を描くと，図3のようになる。
$ \ \mathrm {A} \ $点から照明器具を見た見かけの面積の大きさ$ \ S_{\mathrm {p}} \ $は，照明器具の直径が$ \ 0.25 \ \mathrm {m} \ $であるから，
\[
\begin{eqnarray}
S_{\mathrm {p}}&=&\pi r^{2} \\[ 5pt ] &=&3.1416\times \left( \frac {0.25}{2} \right) ^{2} \\[ 5pt ] &≒& 0.049088 \ \mathrm {[m^{2}]} \\[ 5pt ] \end{eqnarray}
\] となり，ワンポイント解説「5.輝度$ \ L \ $」より，照明器具の光度$ \ I \ $は，
\[
\begin{eqnarray}
I&=&LS_{\mathrm {p}} \\[ 5pt ] &=&1067\times 0.049088 \\[ 5pt ] &≒& 52.377　→　52.4 \ \mathrm {[cd]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：リ
照明から$ \ \mathrm {A} \ $点までの距離$ \ r \ $は，
\[
\begin{eqnarray}
r&=&\sqrt {1^{2}+0.75^{2}} \\[ 5pt ] &=&1.25 \ \mathrm {[m]} \\[ 5pt ] \end{eqnarray}
\] であるから，入射角の余弦$ \ \cos \theta \ $は，
\[
\begin{eqnarray}
\cos \theta &=&\frac {1}{1.25} \\[ 5pt ] &=&0.8 \\[ 5pt ] \end{eqnarray}
\] となる。よって，ワンポイント解説「7.水平面照度と鉛直面照度」より，水平面照度$ \ E_{\mathrm {h}} \ $は，
\[
\begin{eqnarray}
E_{\mathrm {h}} &=&\frac {I\cdot \cos^{3}\theta }{h^{2}} \\[ 5pt ] &=&\frac {52.377\cdot 0.8^{3}}{1} \\[ 5pt ] &≒& 26.817　→　26.8 \ \mathrm {[lx]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ロ
ワンポイント解説「3.光度$ \ I \ $」の通り，光束は光度と立体角の積となります。

(4)解答：カ
(3)より照明器具の全光束$ \ \mathit {\Phi }_{\mathrm {A}} \ $は，
\[
\begin{eqnarray}
\mathit {\Phi }_{\mathrm {A}} &=&I \omega \\[ 5pt ] &=&52.377\times 4\pi \\[ 5pt ] &≒& 658.29 \ \mathrm {[lm]} \\[ 5pt ] \end{eqnarray}
\] であり，図3の室内の総面積$ \ S_{\mathrm {A}} \ $は
\[
\begin{eqnarray}
S_{\mathrm {A}} &=&2.7^{2} \times 2 +\left( 2.7\times 2.3\right) \times 4 \\[ 5pt ] &=& 39.42 \ \mathrm {[m^{2}]} \\[ 5pt ] \end{eqnarray}
\] であるので，ワンポイント解説「4.照度$ \ E \ $」より，室内の平均照度$ \ E_{\mathrm {av}} \ $は，
\[
\begin{eqnarray}
E_{\mathrm {av}} &=&\frac {\mathit {\Phi }_{\mathrm {A}}}{S_{\mathrm {A}}} \\[ 5pt ] &=&\frac {658.29}{39.42} \\[ 5pt ] &≒& 16.699　→　16.7 \ \mathrm {[lx]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ハ
題意より，間接照度$ \ E_{\mathrm {i}} \ $による全光束$ \ \mathit {\Phi }_{\mathrm {i}} \ $は，
\[
\begin{eqnarray}
\mathit {\Phi }_{\mathrm {i}} &=&E_{\mathrm {i}}S\cdot \tau \\[ 5pt ] &=&\frac {\phi }{S}\times \frac {\rho }{\left( 1-\rho \right) }\cdot S\cdot \tau \\[ 5pt ] &=&\phi \times \frac {\rho }{\left( 1-\rho \right) }\cdot \tau \\[ 5pt ] &=&810 \times \frac {0.2}{\left( 1-0.2 \right) }\cdot 0.65 \\[ 5pt ] &≒& 131.63 \ \mathrm {[lm]} \\[ 5pt ] \end{eqnarray}
\] であるから，相互反射による光束$ \ \mathit {\Phi }_{\mathrm {i}} \ $の照明器具の全光束$ \ \mathit {\Phi }_{\mathrm {A}} \ $に占める割合は，
\[
\begin{eqnarray}
\frac {\mathit {\Phi }_{\mathrm {i}}}{\mathit {\Phi }_{\mathrm {A}}}\times 100 &=&\frac {131.63}{658.29}\times 100 \\[ 5pt ] &≒& 20.0 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。