《機械》〈電動機応用〉[H26:問5]空隙付き鉄心リアクトルに関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，リアクトルに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。

インダクタンス$ \ L \ $が$ \ 20 \ \mathrm {mH} \ $の空隙付き鉄心リアクトルがある。このリアクトルの磁路の断面積$ \ S \ $は$ \ 100 \ \mathrm {cm} ^{2} \ $であり，巻線の巻数$N$は$256$である。$ \ S \ $は全磁路にわたって一定で，漏れ磁束，鉄心の飽和，残留磁束などは無視できるものとする。また，巻線の抵抗は無視できるものとする。

このリアクトルに実効値$ \ V=400 \ \mathrm {V}$，$f=50 \ \mathrm {Hz} \ $の正弦波交流電圧を印加したとき，定常状態における鉄心の最大磁束密度は$ \ B_{\mathrm {m}}=\fbox {　（１）　} \ \mathrm {T} \ $となる。

このリアクトルに直流電流$ \ I_{\mathrm {d}}=100 \ \mathrm {A} \ $を通電したとき，鉄心の磁束密度は$ \ B_{\mathrm {d}}=\fbox {　（２）　} \ \mathrm {T} \ $となる。

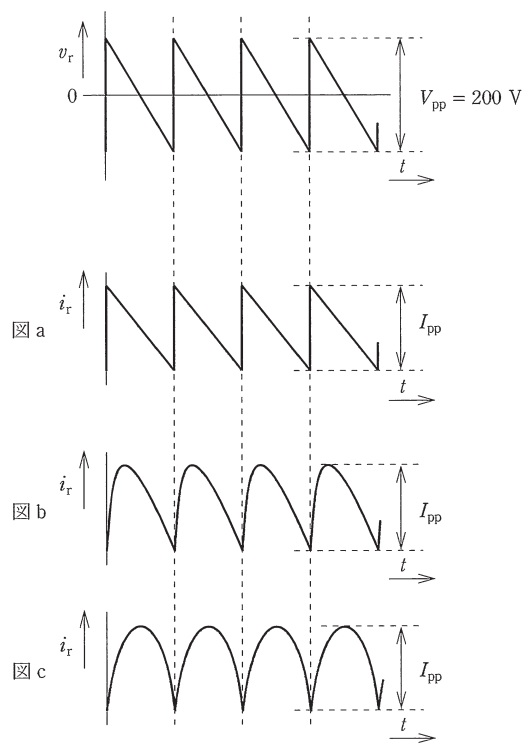
図の最上段に示すような，ピークピーク値$ \ V_{\mathrm {pp}} \ $が$ \ 200 \ \mathrm {V} \ $で周波数が$ \ 300 \ \mathrm {Hz} \ $ののこぎり波電圧$ \ v_{\mathrm {r}} \ $をこのリアクトルに加えた。このときの電流$ \ i_{\mathrm {r}} \ $の波形に最も近い波形は$\fbox {　（３）　}$であり，$ \ i_{\mathrm {r}} \ $のピークピーク値$ \ I_{\mathrm {pp}} \ $は$\fbox {　（４）　} \ \mathrm {A} \ $である。

のこぎり波電圧の$ \ 300 \ \mathrm {Hz} \ $成分の実効値は，$ \ 45.0 \ \mathrm {V} \ $であった。このときの電流の$ \ 300 \ \mathrm {Hz} \ $成分の実効値は$\fbox {　（５）　} \ \mathrm {A} \ $である。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　3.38　　　　　&（ロ）&　0.703　　　　　&（ハ）&　4.16 \\[ 5pt ] &（ニ）&　5.89　　　　　&（ホ）&　2.00　　　　　&（ヘ）&　0.497 \\[ 5pt ] &（ト）&　図　\mathrm {b}　　　　　&（チ）&　7.16　　　　　&（リ）&　200 \\[ 5pt ] &（ヌ）&　図　\mathrm {a}　　　　　&（ル）&　8.33　　　　　&（ヲ）&　0.00703 \\[ 5pt ] &（ワ）&　図　\mathrm {c}　　　　　&（カ）&　0.781　　　　　&（ヨ）&　1.19
\end{eqnarray}
\]

【ワンポイント解説】

機械科目というより，理論科目の電磁気に近いような問題です。配点が高く計算問題で解答が絞れないので，非常に点数差の開く問題となります。計算間違い等ない様確実に理解するようにして下さい。

1.ファラデーの電磁誘導の法則
巻数$ \ N \ $のコイルを貫通する磁束$ \ \phi \ $があるとき，コイルに発生する誘導起電力$ \ e \ $は，
\[
\begin{eqnarray}
e&=& -N\frac {\mathrm {d}\phi }{\mathrm {d}t} \\[ 5pt ] \end{eqnarray}
\] で求められます。

2.磁束$ \ \phi \ $と磁束密度$ \ B \ $の関係
コイルの断面積が$ \ S \ $である時，磁束$ \ \phi \ $と磁束密度$ \ B \ $には，
\[
\begin{eqnarray}
\phi &=& BS \\[ 5pt ] \end{eqnarray}
\] の関係があります。

3.磁束$ \ \phi \ $とコイルに流れる電流$ \ I \ $の関係
巻数$ \ N \ $，自己インダクタンス$ \ L \ $のコイルの磁束$ \ \phi \ $とコイルに流れる電流$ \ I \ $の関係は，
\[
\begin{eqnarray}
N\phi &=& LI \\[ 5pt ] \end{eqnarray}
\] の関係があります。

【解答】

(1)解答：ロ
ワンポイント解説「1.ファラデーの電磁誘導の法則」より，電源電圧$ \ V \ $と巻線を貫く磁束$ \ \phi \ $の関係は，
\[
\begin{eqnarray}
V&=& -N\frac {\mathrm {d}\phi }{\mathrm {d}t} \\[ 5pt ] \end{eqnarray}
\] の関係がある。ここで，$ \ V \ $は実効値が$ \ 400 \ \mathrm {V} \ $の正弦波交流であるから，
\[
\begin{eqnarray}
V&=& 400\sqrt {2}\sin 2\pi f t \\[ 5pt ] \end{eqnarray}
\] で表すことができるため，これを代入し，変数分離により$ \ \phi \ $を求めると，
\[
\begin{eqnarray}
400\sqrt {2}\sin 2\pi f t &=& -N\frac {\mathrm {d}\phi }{\mathrm {d}t} \\[ 5pt ] \mathrm {d}\phi &=& -\frac {400\sqrt {2}}{N}\sin 2\pi f t \ \mathrm {d}t \\[ 5pt ] \phi &=& -\frac {400\sqrt {2}}{N}\int \sin 2\pi f t \ \mathrm {d}t \\[ 5pt ] &=& \frac {400\sqrt {2}}{2\pi f N}\cos 2\pi f t \\[ 5pt ] \end{eqnarray}
\] となる。ワンポイント解説「2.磁束$ \ \phi \ $と磁束密度$ \ B \ $の関係」より磁束密度$ \ B \ $の大きさは，
\[
\begin{eqnarray}
B &=& \frac {\phi }{S} \\[ 5pt ] &=& \frac {400\sqrt {2}}{2\pi f NS}\cos 2\pi f t \\[ 5pt ] \end{eqnarray}
\] となるので，最大磁束密度$ \ B_{\mathrm {m}} \ $は$ \ \cos 2\pi f t =1 \ $の時，
\[
\begin{eqnarray}
B_{\mathrm {m}} &=& \frac {400\sqrt {2}}{2\pi f NS}\\[ 5pt ] &=& \frac {400\sqrt {2}}{2\pi \times 50\times 256\times 0.01} \\[ 5pt ] &≒& 0.703 \ \mathrm {[T]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：カ
ワンポイント解説「3.磁束$ \ \phi \ $とコイルに流れる電流$ \ I \ $の関係」より，
\[
\begin{eqnarray}
N\phi &=& LI_{\mathrm {d}} \\[ 5pt ] NB_{\mathrm {d}}S &=& LI_{\mathrm {d}} \\[ 5pt ] B_{\mathrm {d}} &=& \frac {LI_{\mathrm {d}}}{NS} \\[ 5pt ] \end{eqnarray}
\] となるので，各値を代入すると，
\[
\begin{eqnarray}
B_{\mathrm {d}} &=& \frac {LI_{\mathrm {d}}}{NS} \\[ 5pt ] &=& \frac {20\times 10^{-3}\times 100}{256\times 0.01} \\[ 5pt ] &≒& 0.781 \ \mathrm {[T]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ワ
ワンポイント解説「1.ファラデーの電磁誘導の法則」「3.磁束$ \ \phi \ $とコイルに流れる電流$ \ I \ $の関係」より
\[
\begin{eqnarray}
v_{\mathrm {r}}&=& -N\frac {\mathrm {d}\phi }{\mathrm {d}t} \\[ 5pt ] &=& -L\frac {\mathrm {d}i_{\mathrm {r}} }{\mathrm {d}t} \\[ 5pt ] \end{eqnarray}
\] の関係がある。ここで，上式の正負の符号は電流の向きを表すものであるから，大きさの波形として最も適当なのは，$ \ v_{\mathrm {r}} \ $が零の時，傾きが零となる図(c)となる。

(4)解答：ハ
$ \ v_{\mathrm {r}} \ $は周期が$ \ \displaystyle \frac {1}{300} \ \mathrm {[s]} \ $ののこぎり波であるので，$ \ \displaystyle 0≦t≦\frac {1}{300} \ $において，$ \ t=0 \ $の時$ \ v_{\mathrm {r}}=100 \ $，$ \ \displaystyle t=\frac {1}{300} \ $の時$ \ v_{\mathrm {r}}=-100 \ $であるから，
\[
\begin{eqnarray}
v_{\mathrm {r}}&=& -60000 t +100\\[ 5pt ] \end{eqnarray}
\] となる。よって，(3)より変数分離により，電流を求めると，
\[
\begin{eqnarray}
v_{\mathrm {r}}&=&-L\frac {\mathrm {d}i_{\mathrm {r}} }{\mathrm {d}t} \\[ 5pt ] \mathrm {d}i_{\mathrm {r}} &=&-\frac {1}{L}v_{\mathrm {r}} \mathrm {d}t \\[ 5pt ] &=&-\frac {1}{L}\left( -60000 t +100\right) \mathrm {d}t \\[ 5pt ] i_{\mathrm {r}}&=&-\frac {1}{L}\int \left( -60000 t +100\right) \mathrm {d}t \\[ 5pt ] &=&-\frac {1}{L}\left( -30000 t^{2} +100 t \right) + C（Cは積分定数)\\[ 5pt ] \end{eqnarray}
\] となる。$ \ t=0 \ $を基準電流とすれば，
\[
\begin{eqnarray}
i_{\mathrm {r}}\left( t \right) &=&-\frac {1}{L}\left( -30000 t^{2} +100 t \right) \\[ 5pt ] \end{eqnarray}
\] となるので，$ \ I_{\mathrm {pp}} \ $の大きさは，
\[
\begin{eqnarray}
I_{\mathrm {pp}}&=&\left| i_{\mathrm {r}}\left( \frac {1}{600} \right) – i_{\mathrm {r}}\left( 0 \right)\right| \\[ 5pt ] &=&\left| -\frac {1}{20\times 10^{-3}}\left[ -30000 \times \left( \frac {1}{600}\right) ^{2} +100\times \left( \frac {1}{600}\right) \right] +0\right| \\[ 5pt ] &≒& 4.1667 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。
（※・・・近似計算の方法の違いにより$ \ 4.16 \ $が解答となっていると思われます。）

(5)解答：ヨ
電流の実行値$ \ I \ $は，
\[
\begin{eqnarray}
I&=&\left| \frac {V}{\mathrm {j}\omega L}\right| \\[ 5pt ] &=&\frac {45}{2\pi \times 300 \times 20\times 10^{-3}} \\[ 5pt ] &≒& 1.19 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。