【問題】
【難易度】★★★☆☆(普通)
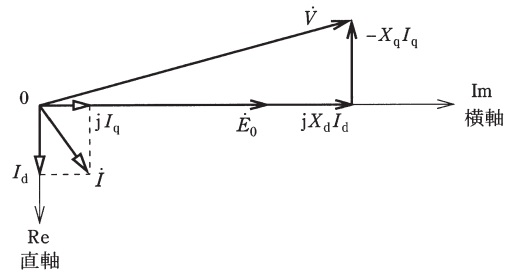
定格周波数\( \ 50 \ \mathrm {Hz} \ \)における磁石の磁極方向の直軸同期リアクタンスが\( \ X_{\mathrm {d}}= 1 \ \Omega \ \),磁極に対して電気角\( \ 90 \ \)度進み方向の横軸同期リアクタンスが\( \ X_{\mathrm {q}}= 2 \ \Omega \ \)の埋込永久磁石同期電動機がある。はじめに同期電動機の電機子巻線を開放し,回転速度\( \ 1 \ 500 \ \mathrm {{min} ^{-1}} \ \)で回転させたとき,磁極方向を実軸とすると,電機子巻線には相電圧\( \ {\dot E}_{0}=\mathrm {j}200 \ \mathrm {V} \ \),\( \ f=50 \ \mathrm {Hz} \ \)の平衡三相交流電圧が現れた。次に,周波数を\( \ f=50 \ \mathrm {Hz} \ \)一定で,相電圧\( \ V \ \mathrm {[V]} \ \)を自由に調整できる平衡三相交流電源に接続して運転する。次の問に答えよ。ただし,巻線抵抗による電圧降下や鉄損は無視できるものとする。また,図は突極性がある同期電動機のフェーザ図である。
(1) 負荷トルクが\( \ T_{1} \ \mathrm {[N\cdot m]} \ \)のとき,交流電源の相電圧\( \ V \ \)を調整すると,電機子巻線には\( \ \dot I =\mathrm {j}50 \ \mathrm {A} \ \)の電流が流れた。このときの\( \ V \ \mathrm {[V]} \ \)を求めよ。
(2) 上記(1)の場合の機械出力\( \ P_{1} \ \mathrm {[kW]} \ \)及びトルク\( \ T_{1} \ \mathrm {[N\cdot m]} \ \)を求めよ。
(3) 交流電源の相電圧\( \ V \ \)を調整して,電機子巻線に実効値\( \ I=50 \ \mathrm {A} \ \)で\( \ \dot I =-10+\mathrm {j}10\sqrt {24} \ \mathrm {A} \ \)の電流を流した。このときの相電圧\( \ V \ \mathrm {[V]} \ \)と発生するトルク\( \ T_{2} \ \mathrm {[N\cdot m]} \ \)を求めよ。
(4) 電機子電流の実効値が\( \ I=50 \ \mathrm {A} \ \)のときに,発生するトルクが最大となる電流\( \ \dot I \mathrm {[A]} \ \)を示せ。
【ワンポイント解説】
直軸同期リアクタンスと横軸同期リアクタンスから電動機のトルクと出力を求める問題ですが,中身はベクトル計算の問題となっています。(4)が時間がかかりそうですが,計算が得意な方は比較的容易に解くことができるかもしれません。
1.掛け算の微分
\( \ f(x)=u(x)v(x) \ \)である時,その微分\( \ f^{\prime }(x) \ \)は,
\[
\begin{eqnarray}
f^{\prime }(x)&=&u^{\prime }(x)v(x) +u(x)v^{\prime }(x) \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)電機子巻線に\( \ \dot I =\mathrm {j}50 \ \mathrm {A} \ \)の電流が流れたときの\( \ V \ \mathrm {[V]} \ \)
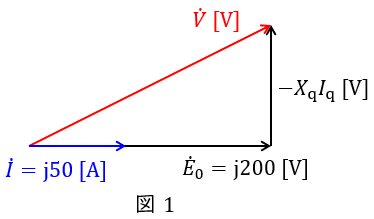
題意に沿ってフェーザ図を描くと図1のようになる。
図1より,
\[
\begin{eqnarray}
-X_{\mathrm {q}}I_{\mathrm {q}}&=&-2\times 50 \\[ 5pt ]
&=&-100 \ \mathrm {[\mathrm {V}]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,このときの\( \ V \ \mathrm {[V]} \ \)の大きさは,
\[
\begin{eqnarray}
V&=&\sqrt {\left( -X_{\mathrm {q}}I_{\mathrm {q}}\right) ^{2} +E_{0}^{2}} \\[ 5pt ]
&=&\sqrt {\left( -100\right) ^{2} +200^{2}} \\[ 5pt ]
&≒&223.61 → 224 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)(1)の場合の機械出力\( \ P_{1} \ \mathrm {[kW]} \ \)及びトルク\( \ T_{1} \ \mathrm {[N\cdot m]} \ \)
(1)の場合の電力\( \ P_{1}+\mathrm {j}Q_{1} \ \)は,遅れ無効電力を正とすると,
\[
\begin{eqnarray}
P_{1}+\mathrm {j}Q_{1}&=&3\dot V \overline {\dot I} \\[ 5pt ]
&=&3\times \left( -100 +\mathrm {j}200\right) \times \left( -\mathrm {j}50\right) \\[ 5pt ]
&=&30 \ 000+\mathrm {j}15 \ 000 \ \mathrm {[V\cdot A]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,機械出力\( \ P_{1} \ \)は,
\[
\begin{eqnarray}
P_{1}&=&30 \ 000 → 30 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。またトルク\( \ \displaystyle T_{1}=\frac {P_{1}}{\omega } \ \)であり,
\[
\begin{eqnarray}
\omega &=&\frac {2\pi N}{60} \\[ 5pt ]
&=&\frac {2\pi \times 1 \ 500}{60} \\[ 5pt ]
&≒&157.08 \ \mathrm {[{min} ^{-1}]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
T_{1} &=&\frac {P_{1}}{\omega } \\[ 5pt ]
&=&\frac {30 \ 000}{157.08 } \\[ 5pt ]
&≒&190.99 → 191 \ \mathrm {[N\cdot m]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)実効値\( \ I=50 \ \mathrm {A} \ \)で\( \ \dot I =-10+\mathrm {j}10\sqrt {24} \ \mathrm {A} \ \)の電流を流したときの相電圧\( \ V \ \mathrm {[V]} \ \)と発生するトルク\( \ T_{2} \ \mathrm {[N\cdot m]} \ \)
電機子電流\( \ \dot I = I_{\mathrm {d}}+\mathrm {j}I_{\mathrm {q}}=-10+\mathrm {j}10\sqrt {24} \ \)であるから,
\[
\begin{eqnarray}
\mathrm {j}X_{\mathrm {d}}I_{\mathrm {d}}&=&\mathrm {j}1\times \left( -10\right) \\[ 5pt ]
&=&-\mathrm {j}10 \ \mathrm {[\mathrm {V}]} \\[ 5pt ]
-X_{\mathrm {q}}I_{\mathrm {q}}&=&-2\times 10\sqrt {24} \\[ 5pt ]
&=&-20\sqrt {24} \ \mathrm {[\mathrm {V}]} \\[ 5pt ]
\end{eqnarray}
\]
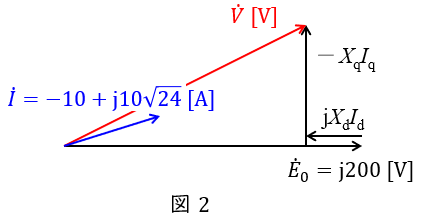
となるので,ベクトル図を描くと図2のようになる。よって,相電圧\( \ \dot V \ \)は,
\[
\begin{eqnarray}
\dot V&=&-X_{\mathrm {q}}I_{\mathrm {q}}+E_{0}+\mathrm {j}X_{\mathrm {d}}I_{\mathrm {d}} \\[ 5pt ]
&=&-20\sqrt {24}+\mathrm {j}200-\mathrm {j}10 \\[ 5pt ]
&=& -20\sqrt {24}+\mathrm {j}190 \ \mathrm {[\mathrm {V}]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,その大きさは,
\[
\begin{eqnarray}
V&=&\sqrt {\left( -20\sqrt {24}\right) ^{2} + 190^{2}} \\[ 5pt ]
&≒& 213.78 \ \mathrm {[\mathrm {V}]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,その時の電力\( \ P_{2}+\mathrm {j}Q_{2} \ \)は,
\[
\begin{eqnarray}
P_{2}+\mathrm {j}Q_{2}&=&3\dot V \overline {\dot I} \\[ 5pt ]
&=&3\times \left( -20\sqrt {24}+\mathrm {j}190\right) \times \left( -10-\mathrm {j}10\sqrt {24}\right) \\[ 5pt ]
&≒&30 \ 864+\mathrm {j}8 \ 700 \ \mathrm {[V\cdot A]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,求めるトルク\( \ T_{2} \ \)は,
\[
\begin{eqnarray}
T_{2} &=&\frac {P_{2}}{\omega } \\[ 5pt ]
&=&\frac {30 \ 864}{157.08 } \\[ 5pt ]
&≒&196.49 → 196 \ \mathrm {[N\cdot m]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)電機子電流の実効値が\( \ I=50 \ \mathrm {A} \ \)のときに,発生するトルクが最大となる電流\( \ \dot I \mathrm {[A]} \ \)
電機子電流\( \ \dot I =I\cos \theta +\mathrm {j}I\sin \theta =50\cos \theta +\mathrm {j}50\sin \theta \ \)とおく。このとき,
\[
\begin{eqnarray}
\mathrm {j}X_{\mathrm {d}}I_{\mathrm {d}}&=&\mathrm {j}1\times 50\cos \theta \\[ 5pt ]
&=&\mathrm {j}50\cos \theta \ \mathrm {[\mathrm {V}]} \\[ 5pt ]
-X_{\mathrm {q}}I_{\mathrm {q}}&=&-2\times 50\sin \theta \\[ 5pt ]
&=&-100\sin \theta \ \mathrm {[\mathrm {V}]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,相電圧\( \ \dot V \ \)は,
\[
\begin{eqnarray}
\dot V&=&-X_{\mathrm {q}}I_{\mathrm {q}}+E_{0}+\mathrm {j}X_{\mathrm {d}}I_{\mathrm {d}} \\[ 5pt ]
&=& -100\sin \theta +\mathrm {j}\left( 200 +50\cos \theta \right) \ \mathrm {[\mathrm {V}]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,その時の電力\( \ P_{3}+\mathrm {j}Q_{3} \ \)は,
\[
\begin{eqnarray}
P_{3}+\mathrm {j}Q_{3}&=&3\dot V \overline {\dot I} \\[ 5pt ]
&=&3\times \left[ -100\sin \theta +\mathrm {j}\left( 200 +50\cos \theta \right) \right] \times \left( 50\cos \theta -\mathrm {j}50\sin \theta \right) \\[ 5pt ]
&=&-7 \ 500\sin \theta \cos \theta +30 \ 000\sin \theta +\mathrm {j}\left( 30 \ 000\cos \theta +7 \ 500\cos ^{2}\theta +15 \ 000\sin ^{2} \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
となるので,出力\( \ P_{3} \ \)は,
\[
\begin{eqnarray}
P_{3}&=&-7 \ 500\sin \theta \cos \theta +30 \ 000\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,トルクが最大になる時,出力も最大となるから,\( \ \displaystyle \frac {\mathrm {d}P_{3}}{\mathrm {d}\theta }=0 \ \)となる\( \ \theta \ \)を求めればよい。
\[
\begin{eqnarray}
\frac {\mathrm {d}P_{3}}{\mathrm {d}\theta }=-7 \ 500\left( \cos ^{2} \theta -\sin ^{2}\theta \right) +30 \ 000\cos \theta &=& 0 \\[ 5pt ]
-7500\left( 2\cos ^{2} \theta -1\right) +30 \ 000\cos \theta &=& 0 \\[ 5pt ]
2\cos ^{2} \theta -4\cos \theta -1 &=& 0 \\[ 5pt ]
\cos \theta &=& \frac {2±\sqrt {4+2}}{2} \\[ 5pt ]
&=& -0.224 \ 74,2.224 \ 7(不適) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,\( \ \sin \theta \ \)は,
\[
\begin{eqnarray}
\sin \theta &=& \sqrt {1-\cos \theta } \\[ 5pt ]
&=& \sqrt {1-\left( -0.224 \ 74\right) ^{2}} \\[ 5pt ]
&=& 0.974 \ 42 \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,求める電機子電流\( \ \dot I \ \)は,
\[
\begin{eqnarray}
\dot I &=& 50\cos \theta +\mathrm {j}50\sin \theta \\[ 5pt ]
&=& 50\times \left( -0.224 \ 74 \right) +\mathrm {j}50 \times 0.974 \ 42 \\[ 5pt ]
&=& -11.237 +\mathrm {j}48.721 → -11.2+\mathrm {j}48.7 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん